To initially test that the D&C algorithm returns an acceptable approximation of
the density matrix, a simple test case was used. The D&C algorithm is most
appropriate for weakly interacting systems. Long range Coulombic interactions
are not yet included in the CRYSTAL implementation and periodic covalently
bonded systems cause inconsistencies in the subsystems' electronic structure,
see Section 6. A 10 Å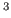 box of neon atoms created using a
short classical molecular dynamics simulation1 was used as a
test case, see Figure 2.
box of neon atoms created using a
short classical molecular dynamics simulation1 was used as a
test case, see Figure 2.
Figure 2:
The system used to test that the density matrix partitioning and
reconstruction functioned correctly. 10 Å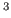 of neon atoms in positions
determined by a short classical molecular dynamics computation.
of neon atoms in positions
determined by a short classical molecular dynamics computation.
|
|
The system was partitioned into subsystems using one core-atom subsystems, and
a set of partition matrices as defined in Equation (4). The
convergence of the system energy as a function of halo radius is reported in
Table 1. It can be seen that as the size of the halo is
increased the energy converges on the result of the traditional Hamiltonian
diagonalisation used in standard CRYSTAL calculations. This is unsurprising
considering the weak interatomic interactions in this system, but indicates
that the divide and conquer implementation correctly partitions the system and
reconstructs the density matrix based on the subsystem computations.
Table 1:
Convergence on the DFT energy for the D&C algorithm as the radius of
the halo increases.
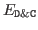 is the energy computed using the D&C
algorithm,
is the energy computed using the D&C
algorithm,
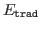 is the energy computed using Hamiltonian Matrix
diagonalisation -- the standard CRYSTAL algorithm.
is the energy computed using Hamiltonian Matrix
diagonalisation -- the standard CRYSTAL algorithm.
 |
Daniel R. Jones 2011-12-06

