Divide and Conquer Algorithm

The divide and conquer algorithm (D&C), is a relatively old idea [11] that is ideally suited to current HPC resources as there is significantly more computation than communication. Conceptually, it is a relatively simple scheme, using the ``near-sightedness'' of electrons, one can separate a system into subsystems comprising a core region and a halo region, as shown in Figure 1. The subsystems are decoupled, and the electronic structure of each subsystem is determined independently. The systems are then reconnected by identifying a common Fermi energy and a new global density matrix, from which the system's total energy can be easily computed, is constructed by adding the contributions from the core regions. The electronic structure of the halo is discarded. The presence of the halo region is just to ensure the electronic structure of the core region is as close as possible to that of the reconstructed system.

Figure: The system is partitioned into a set of subsystems, $\left\lbrace \alpha \right\rbrace$, each subsystem contains a core region $\Omega _0\alpha$ and a halo region $\Gamma _2\alpha$ and, optionally, a region which contributes partially, $\Gamma _1\alpha$. The electronic structure of the subsystems is determined independently and from these computations the global electronic structure is reconstructed. Figure from ref. [12].

More formally, a computation to calculate the single point energy of a system $\Omega$, whose single particle wavefunctions are written as a linear combination of a localised basis set, $\left\lbrace i \right\rbrace$, can be approximately solved by dividing $\Omega$ into a set of subsystems, $\left\lbrace \alpha \right\rbrace$, and defining a partition matrix

$$\mathbf{P}_{ij} = \sum_\alpha \mathbf{P}_{ij}^{\alpha} = 1.$$ (1)

Once the electronic structure of the independent subsystems has been determined, using a traditional DFT or HF algorithm, a global Fermi energy must be identified that returns the (known) correct number of electrons, $N_{el}$. In the case of a non-magnetic system, where all electrons are paired,

$$N_{el} = \sum_{ij} \rho_{ij} \mathbf{S}_{ij} = \sum_{ij} \left( 2... ...\mathbf{C}_{im}^\alpha \mathbf{C}_{jm}^{\alpha\dagger} \right) \mathbf{S}_{ij},$$ (2)

where $\rho_{ij}$ is the (global) density matrix, $\mathbf{S}_{ij}=\left\langle i \middle\vert j \right\rangle$ is the overlap matrix, $f_\beta$ is the Fermi function at an arbitrary electronic temperature $\beta$ and $\mathbf{C}_{im}^\alpha$ is the matrix representation of the eigenfunctions of subsystem $\alpha$. The Fermi energy $\varepsilon_F$ that satisfies (2) is found iteratively. Once the Fermi energy has been identified, the density matrix for the system can be computed by summing the contributions from the subsystems, $\left\lbrace \alpha \right\rbrace$,

$$\rho_{ij} = 2 \sum_\alpha \mathbf{P}_{ij}^\alpha \sum_m f_\beta \... ...- \varepsilon_m \right) \mathbf{C}_{im}^\alpha \mathbf{C}_{jm}^{\alpha\dagger}.$$ (3)

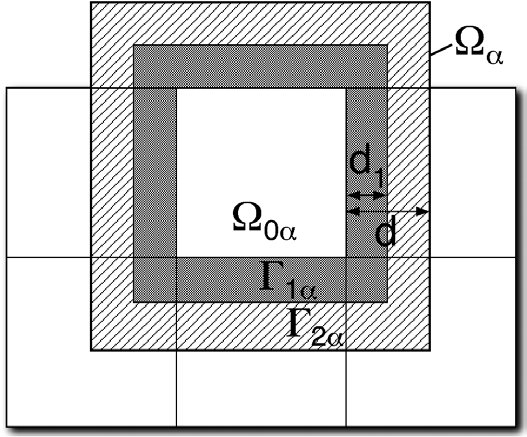
The accuracy of the electronic structure computed using this method varies depending on the partitioning of the system into subsystems. During this dCSE project, two methods for partitioning the system have been implemented. The simplest, most conservative method is for each subsystem to contain a single core atom. This method has been implemented in SIESTA [10] and is equivalent to a Mulliken population analysis. This method has a single parameter, the radius of the halo around the core atom. The appropriate size for the halo depends on the material being studied and can be defined in the CRYSTAL input file. The partition matrix for the system is defined as follows:

$$\mathbf{P}_{ij}^\alpha = \begin{cases}1, &\mbox{if } i \in \Omega... ... &\mbox{if } i \ni \Omega_{\alpha} \wedge j \ni \Omega_{\alpha}, \end{cases}$$ (4)

where $\Omega_\alpha$ is the set of basis functions centred on the core atom. This very simple partitioning of the system is likely to be quite inefficient, it is simple to improve performance by including several atoms in the core region of each subsystem. However, it has been noted that having multiple core atoms per subsystem may increase the likelihood of having discontinuities in the potential energy surface [10]. One core atom per subsystem is the safest default option.

The alternative solution implemented in CRYSTAL (during this dCSE project) is to leave the definition to the user and explicitly define each subsystem by selecting a set of atoms (or ghost atoms) and defining the partition matrix in atom-by-atom terms by hand. The way it has been implemented, $\mathbf{P}_{ij} ^\alpha$ must be identical for all basis functions localised on the same atom. This allows users to have the flexibility to use the D&C algorithm in the way that is most suited to their problem. The code which partitions the systems into subsystems has been designed so that new heuristics for defining the partition matrix can be added at a later date without altering the structure of the code. The newly implemented D&C algorithm simply needs a mapping array, which associates atoms in the subsystems with atoms in the reconstructed system, and a partition matrix for each subsystem. The $\mathbf{P}_{ij} ^\alpha$ matrices defined must satisfy Equation (1).

In the time available, point 4 on the list of milestones has not yet been addressed. The long range electrostatics of the system have been discarded, for systems that are largely non-polar, this should make no difference and the electrostatics included by the interaction of the core with the halo region should be sufficient, as will be shown in the next section.