Performance Tests

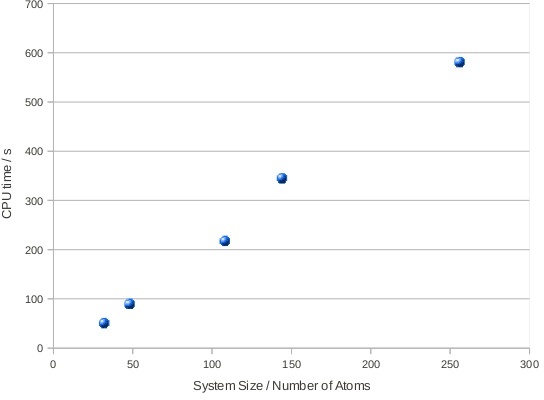
To measure the performance of the D&C algorithm with increasing system size, the density matrix was computed for various supercells of crystalline neon with a face centred cubic crystal structure (from the Inorganic Crystal Structure Database [14]). The time taken to compute the density matrix with varying systems size is shown in Figure 3. The scaling is nearly linear. 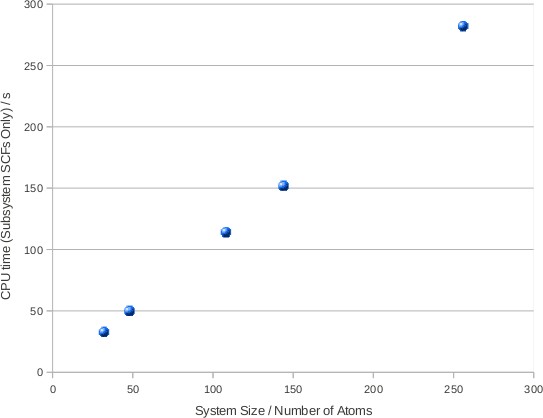The non-linear part of the scaling comes from computing the Fermi energy for the system. Figure 4 shows the time taken to set up and compute the electronic structure of the subsystems. This shows almost perfect linear scaling, and also shows that a substantial part of the run time is spent computing the Fermi energy. Improvements to the algorithm to compute the Fermi energy should be a priority in the continuation of this work.

Figure 3: The time taken to compute the density matrix using the divide and conquer algorithm as a function of system size. The algorithm displays near linear scaling.

Figure 4: The CPU time taken to converge the SCF for all subsystems using the D&C algorithm. This shows near perfect linear scaling. Further investigation is needed to reduce the time taken to calculate the Fermi energy for the system.