SMM

At the same time, before introducing the recursive multiplication into the main code, another new feature was introduced - a specialised small matrix multiplication library `libsmm'. In CP2K the sizes of the matrix blocks depend on the atomic species being simulation and the basis set. Typically, this results in small blocks with unusual sizes such as 1x4, 5x13, 9x22 etc. Libsmm takes an autotuning approach to producing specialised DGEMM routines for a specified set of small matrix sizes:

Firstly for a set of `tiny' block sizes (typically 1 up to 12) a set of different loop permutations and unrollings is generated for each combination of block sizes (m,n,k), where matrix C is m by n, A is n by k and B is k by m. E.g. for m=2, n=3, k=5 the canonical multiplication loop is:

[frame=single]

      DO j= 1 , 3 , 1
      DO i= 1 , 2 , 1
      DO l= 1 , 5 , 1
        C(i+0,j+0)=C(i+0,j+0)+A(i+0,l+0)*B(l+0,j+0)
      ENDDO
      ENDDO
      ENDDO

There are six possible loop permutations (ijl, jil, ilj, jli, lij, lji) and for each permutation it is possible to unroll any combination of the loops e.g. for the above loop ordering the first three possible unrollings are:

[frame=single]

      DO j= 1 , 3 , 1
      DO i= 1 , 2 , 1
      l= 1
        C(i+0,j+0)=C(i+0,j+0)+A(i+0,l+0)*B(l+0,j+0)
        C(i+0,j+0)=C(i+0,j+0)+A(i+0,l+1)*B(l+1,j+0)
        C(i+0,j+0)=C(i+0,j+0)+A(i+0,l+2)*B(l+2,j+0)
        C(i+0,j+0)=C(i+0,j+0)+A(i+0,l+3)*B(l+3,j+0)
        C(i+0,j+0)=C(i+0,j+0)+A(i+0,l+4)*B(l+4,j+0)
      ENDDO
      ENDDO

      j= 1
      DO i= 1 , 2 , 1
      DO l= 1 , 5 , 1
        C(i+0,j+0)=C(i+0,j+0)+A(i+0,l+0)*B(l+0,j+0)
        C(i+0,j+1)=C(i+0,j+1)+A(i+0,l+0)*B(l+0,j+1)
        C(i+0,j+2)=C(i+0,j+2)+A(i+0,l+0)*B(l+0,j+2)
      ENDDO
      ENDDO

      j= 1
      DO i= 1 , 2 , 1
      l= 1
        C(i+0,j+0)=C(i+0,j+0)+A(i+0,l+0)*B(l+0,j+0)
        C(i+0,j+0)=C(i+0,j+0)+A(i+0,l+1)*B(l+1,j+0)
        C(i+0,j+0)=C(i+0,j+0)+A(i+0,l+2)*B(l+2,j+0)
        C(i+0,j+0)=C(i+0,j+0)+A(i+0,l+3)*B(l+3,j+0)
        C(i+0,j+0)=C(i+0,j+0)+A(i+0,l+4)*B(l+4,j+0)
        C(i+0,j+1)=C(i+0,j+1)+A(i+0,l+0)*B(l+0,j+1)
        C(i+0,j+1)=C(i+0,j+1)+A(i+0,l+1)*B(l+1,j+1)
        C(i+0,j+1)=C(i+0,j+1)+A(i+0,l+2)*B(l+2,j+1)
        C(i+0,j+1)=C(i+0,j+1)+A(i+0,l+3)*B(l+3,j+1)
        C(i+0,j+1)=C(i+0,j+1)+A(i+0,l+4)*B(l+4,j+1)
        C(i+0,j+2)=C(i+0,j+2)+A(i+0,l+0)*B(l+0,j+2)
        C(i+0,j+2)=C(i+0,j+2)+A(i+0,l+1)*B(l+1,j+2)
        C(i+0,j+2)=C(i+0,j+2)+A(i+0,l+2)*B(l+2,j+2)
        C(i+0,j+2)=C(i+0,j+2)+A(i+0,l+3)*B(l+3,j+2)
        C(i+0,j+2)=C(i+0,j+2)+A(i+0,l+4)*B(l+4,j+2)
      ENDDO

In the case where m,n or k are not prime, it is possible to partially unroll the loops (e.g. a 4-fold loop may be unrolled by 2 or by 4). For the largest block sizes considered (12,12,12) there are 540 permutations that are automatically generated. Each of these variants is then run (for long enough to perform 1 GFLOP) and the performance (GLOP/s) is recorded. The particular loop structure which generated this performance is then recorded.

Recognising that for larger block sizes, the number of combinations to be tested will grow rapidly, in the second stage of autotuning a different set of `small' block sizes are used - these are the sizes that will be supported by the final library, and can be chosen by the user to match block sizes they expect to be used by CP2K as a result of the particular system they are simulating. By default the set of m,n,k are 1, 4, 5, 6, 9, 13, 16, 17 and 22.

Again for each possible combination of m,n,k, a set of 7 multiplication procedures are generated:

• tiny version (or canonical loop, if not available)
• Fortran MATMUL
• Library DGEMM
• 4 recursive variants with base cases terminating in good-performing tiny mults

Similarly to before, each of the permutations is then run (for 10 GLOPs) and the performance is measured. The best variant for each of the small sizes is then compiled into an individual object file and added to the library. Note that in some cases, particularly for large block sizes, library DGEMM may give the best performance. Because of this, CP2K still needs a BLAS library when linking with libsmm in order to resolve these fall-though cases. A wrapper routine is also included such that SMM can be called for any sizes of m,n,k and if these are not supported directly in the library, will call directly to BLAS. The entire library compilation is controlled by a set of scripts and makefiles, allowing it to run in parallel on a single node on the HECToR compute nodes. Compilation of the library took around 2 hours 15 minutes using the default set of `tiny' and `small' sizes.

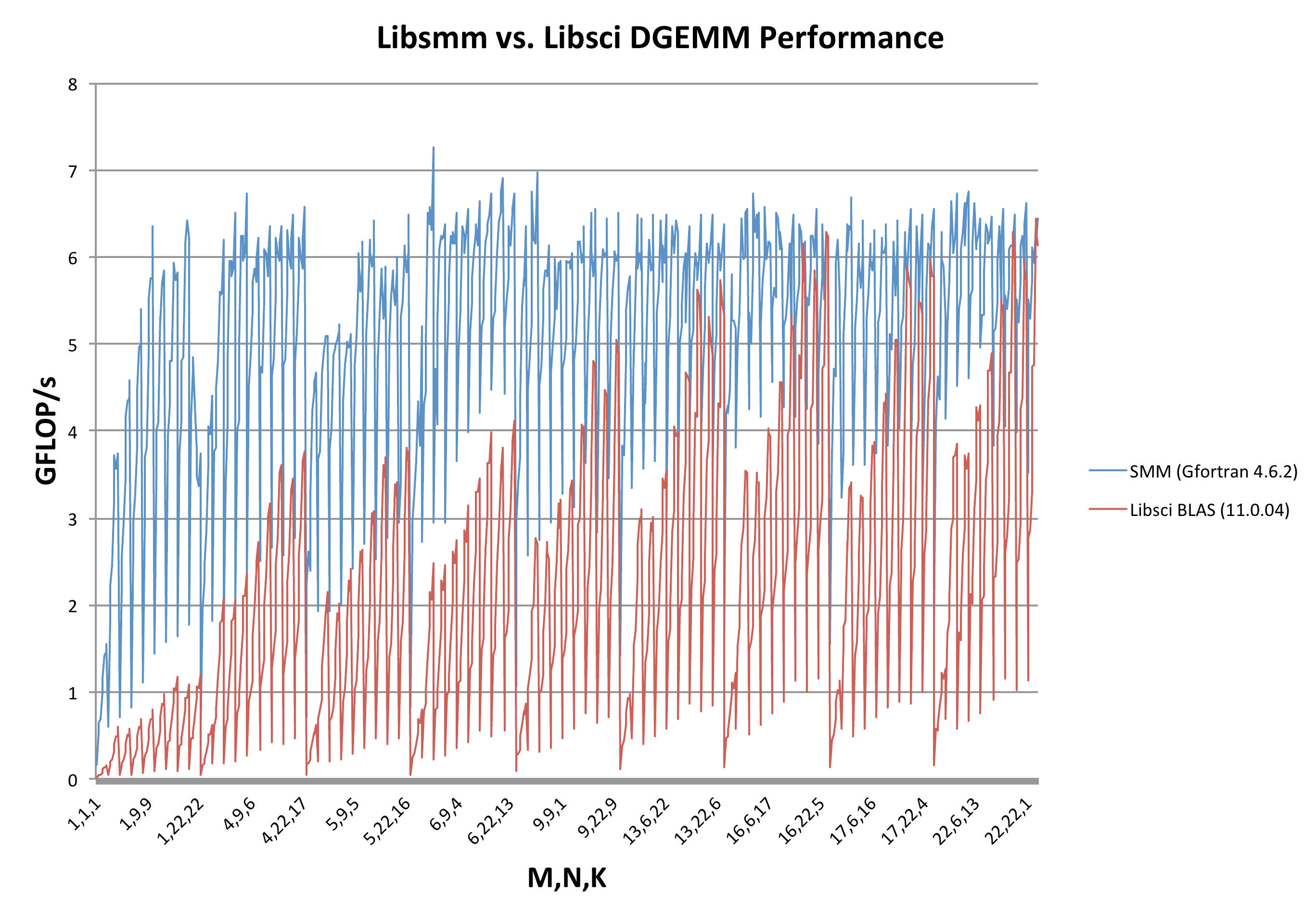
Finally, the library routines are then tested against the supplied BLAS library, both to check performance and correctness. Results of this test are shown in figure 5, taken from a compilation on the XE6 TDS system. Especially for small block sizes (or blocks where one or more dimensions is small) we find that libsmm outperforms the BLAS in Cray's libsci by up to 10 times. Similar results have been found comparing with e.g. MKL on an Intel platform. For larger block sizes, the performance tends towards Libsci BLAS indicating that a faster method could not be found. It should be noted that in the limit of very large blocks (1000x1000), DGEMM achieves around 12.8 GLOP/s, which is around 5.5 FLOPs/cycle, indicating that the library is making use of the AMD Bulldozer architecture's FMA4 instructions since for these tests only a single thread is running.

Figure 5: Comparing performance of SMM and Libsci BLAS for block sizes up to 22,22,22

Libsmm is distributed with the CP2K source package, and a version of the library optimised for the current HECToR Phase 3 `Interlagos' processors can be found in /usr/local/packages/cp2k/2.3.15/libs/libsmm/.