FFT

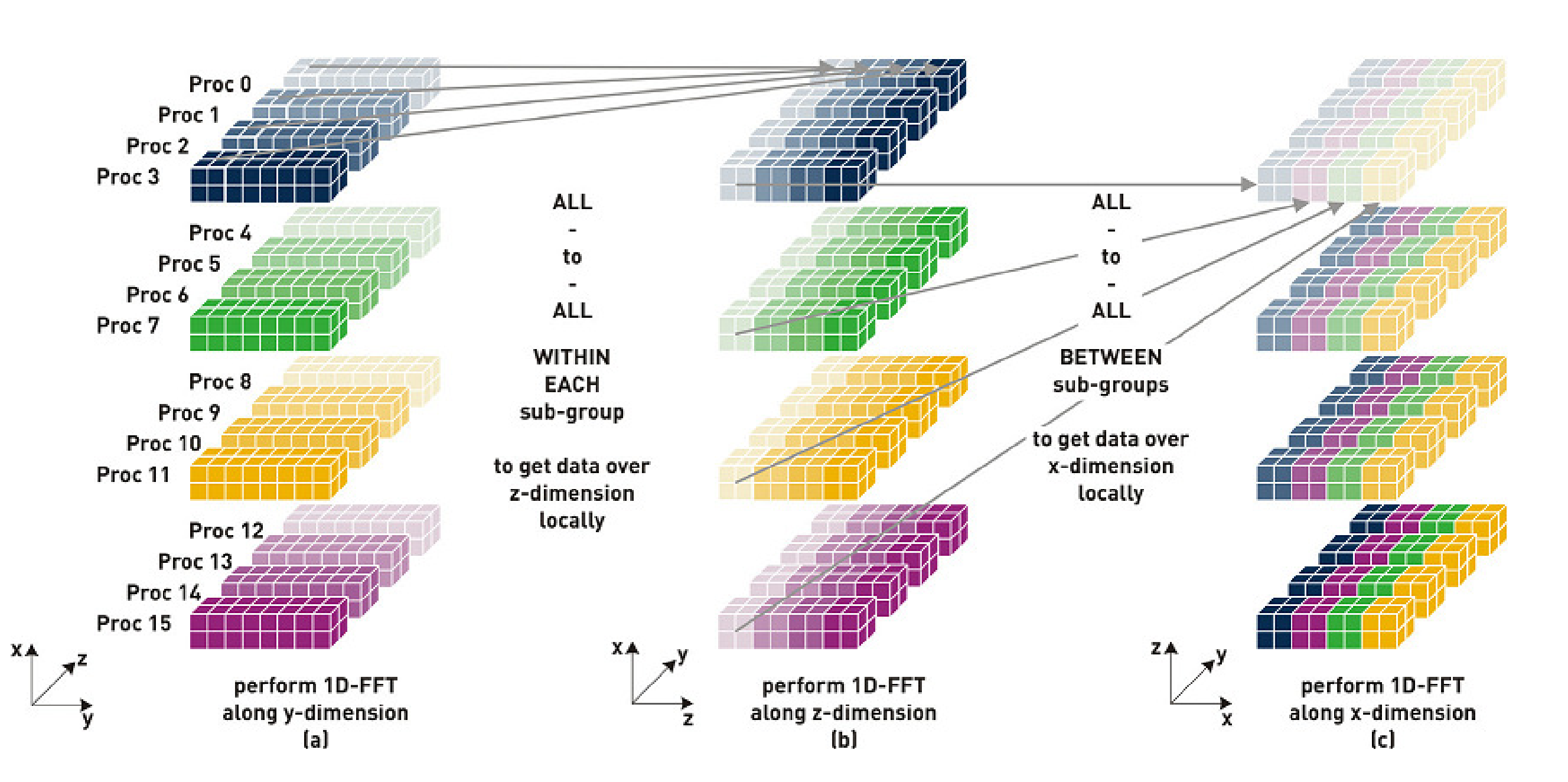
In CP2K, the 3D Fast Fourier Transform (FFT) is a key step in the Quickstep algorithm, efficiently transforming from a real-space representation of e.g. electronic density, or potential, to the fourier-space (or planewave) representation and vice versa. The algorithm involves in general 5 steps (for a 2D-distributed planewave grid - the 1D case requires less). This is illustrated in figure 1, and a fuller discussion of the algorithm can be found e.g. in Jagode 2006[7].

1.

Perform 1D FFT of local data (for example in the Z-direction)

2.

Transpose the data using MPI_Alltoallv to bring the Y-dimensional data local

3.

Perform 1D FFT of local data (Y-direction)

4.

Transpose again using MPI_Alltoallv to bring the X-dimensional data local

5.

Perform 1D FFT of local data (X-direction)

Figure 1: Realspace grid for a single task showing local and halo(shaded) parts of the grid - 2D only

There are two parts of this process that we can parallelise using OpenMP - firstly, the 1D FFT itself, and secondly the packing and unpacking of the buffers used by the MPI_Alltoallv.

For the 1D FFT, each MPI process has to perform a block of M FFTs each of length N. The actual FFT is performed by a call to an FFT library (typically FFTW3[8]), but three different approaches were tested on how to divide up the work between the available threads.

1.

Using FFTW threading - the FFTW3 library has inbuilt threading capability, and it is possible to plan an FFT for a given number of threads. Using this method, the number of OpenMP threads available is found using omp_get_num_threads() and passed to the FFTW planner using fftw_plan_with_nthreads(). Then when the plan is executed the specified number of threads are used.

2.

Parallel loop over single length-N FFTs - here we generate an FFTW plan for a single length-N FFT, running on a single thread. The M FFTs are then performed in a loop, which is parallelised using OpenMP. This results in each thread performing (approximately) the same number of FFTs.

3.

Parallel blocks of  M/nthreads length-N FFTs - similar to the previous approach this requires creation of multiple plans (actually only 1 or 2 are required to cover all cases). Each thread then executes one of the plans starting at an appropriate offset into the data array, and FFTs a set number of rows of data. Some care must be exercised here to ensure that each thread always starts its FFT on an element which is aligned on a 16-byte boundary, due to the requirements for SSE vectorization, but this can be achieved by dividing the array up in pairs of rows if there is an odd number of elements in each row and single precision arithmetic is being used.

As it turns out, the FFTW threading is not particularly efficient, giving only a maximum speedup of 1.7x when using 4 threads on a node compared to only a single thread (on HECToR Phase 2a). The second and third methods perform similarly, with the third slightly better due to the reduced overhead of executing many small FFTs compared to a small number of larger blocks of FFTs. With this method we see a speedup of 2.9x on 4 threads. Part of the reason for not seeing the full 4x speedup in the case is that as well as being computationally intensive, the FFT also requires memory bandwidth as the data is streamed from memory into cache. Adding more threads gives access to more FLOPs but not any additional memory bandwidth as access to memory is shared between all 4 cores. Of course, this is also a problem for the MPI implementation, except the same total bandwidth must be shared between four processes, rather than four threads.

In addition to the FFT itself, OpenMP was also used to parallelise the packing of the MPI buffers for the transpose. In this case some of the loops to be parallelised are perfectly nested and so can be coalesced into a single loop using the OpenMP collapse clause, which increases the iteration space and therefore allows more parallelism to be exploited. This is particularly advantageous where one of the loops is over the number of MPI processes, which may be small (and will be made smaller as more threads are used). However, this feature is only in OpenMP version 3.0, which is not yet supported by all compilers (notably the Pathscale compiler), and so a new preprocessor macro __HAS_NO_OMP_3 is used to turn this feature off for compilers that do not support it.

The final OpenMP-parallel FFT code performs well in benchmarks, proving to be giving the same performance at low core counts, but scaling much better. As shown in figure 2 the peak performance for the 3D FFT of a 125³ grid is at 512 cores for the MPI-only code, 1024 cores when using 2 threads per task, and 2048 cores when using 4 threads per task. Also, the peak performance of the 4-threaded version is 2.8 times higher than that of the MPI-only version, so the increases scalability also delivers real improvements in time-to-solution.

Figure 2: Performance of 125³ FFT on HECToR Phase 2a

Figure 3 shows the equivalent results on Rosa. Here we see a similar trend, however, there is no additional benefit from using more than 6 threads per MPI task. This reflects the fact that the 12-way SMP node on the Cray XT5 is in fact two hexacore chips connected together via a hypertransport bus, and therefore there is a significantly higher penalty for accessing memory in the memory banks attached to the other processor. This results is any benefit of the extra cores in terms of FLOPs available being nullified by the increased memory access latency, and contention in the cache heirarchy. Nevertheless, using 2 MPI processes per node, each with 6 threads appears to be a performant solution, at least for the 3D FFT. It is also worth noting that the FFT as a whole scales worse on Rosa than on HECToR Phase 2a. This is due to the increased number of cores (12 c.f. 4) on a node which share a single SeaStar2+ network interface. Especially in the regime where there are many processes communicating, and the message size is small, the message throughput rate of the SeaStar can become a limiting factor. We will see this effect even more strongly on the 24-core nodes of HECToR Phase 2b.

Figure 3: Performance of 125³ FFT on Rosa