 |
Realspace to Planewave transfer (or rs2pw) is responsible for the halo swap and alltoall communication necessary for transforming between the realspace (replicated or 1D, 2D, 3D distributed) grids and the corresponding (1D or 2D distributed) planewave grids in prepartion for th FFT which transforms the data on the planewave grids into its reciprocal representation. Much of the time spent in this routine is in communication, but there are several loops that can be parallelised using OpenMP. Like the FFT, MPI buffer packing was parallelised, with each thread packing a portion of the buffer with data from the grids and vice versa. Many of these buffer packing operations are conveniently described by Fortran90 array syntax e.g. (pseudocode)
send_buf(:) = rs % r (lb:ub)
This type of operation can be easily parallelised using the Openmp workshare directive, which ensures each thread is responsible for copying a particular subset of the array. However, the GNU implementation of OpenMP (gfortran is a popular compiler for CP2K) prior to the recently released version 4.5.0 implements workshare in the same way as single i.g. serialising the array operation on a single thread. While technically standards-compliant this obviously does not give good performance, so these operations were manually parallelised by defining a given range for each thread based on its thread ID and the array bounds.
Another loop that was parallelised was responsible for calculating the amount of data to be sent to and from each process. This took the form of a nested loop over pairs of processes (see below). However, a conditional inside the loop would only allow the loop body to execute if one of the two indices was the ID of the process in question. So out of the P2 loop iterations, only 2P actually did anything useful. This posed a problem for OpenMP parallelisation, as most iterations of the outer loop would take the same amount of computation (only a single iteration of the inner loop would execute), but one iteration would take P time longer as the entire inner loop would execute.
do i = 1, group_size
do j = 1, group_size
if (i == my_id || j == my_id) then
<do stuff...>
end if
end do
end do
By transforming this nested loop into two independent loops from 1 to group_size not only did it become much easier to efficiently parallelise with OpenMP, it also significantly reduced the amount of time wasted in needless loop iterations even when threads were not used.
Finally, after observing that the following alltoallv is fairly sparse (that is, only a few pairs of processes communicate, rather than an true all-to-all), this was replaced with non-blocking point-to-point MPI operations between the pairs of processes that actually have data to transfer. This gave a speedup of 5-10% over the existing MPI_Alltoallv implementation.
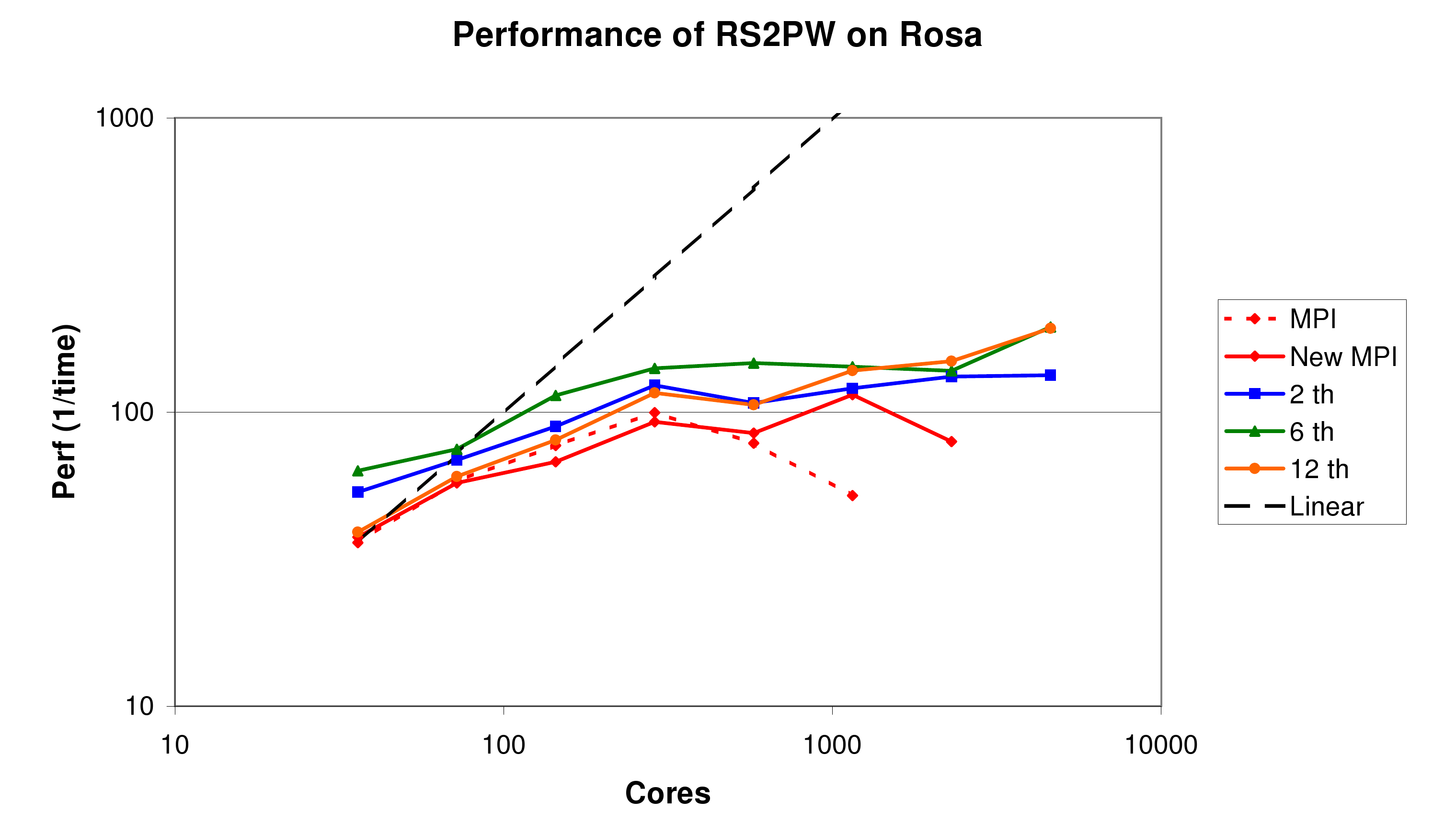
The result of all these optimisations can be seen on the graph below (figure 4). Clearly the algorithm itself does not scale as well as the FFT. However, the impact that the loop restructuring and sparse alltoall have is clear from the difference between the original and `New MPI' results, causing the routine to scale out to 1152 cores for this problem size (1253 realspace grid). Again, using 2 or 6 threads per MPI task gives some improvement both in the raw performance and also the scalability of the code. The best performace overall is achieved using 768 MPI tasks, each with 6 threads. However, this is only twice as fast as the pure MPI code using only 288 cores in total. Nevertheless, by removing the steep drop-off beyond this point seen in the with the original MPI implementation, this will help the code as a whole to scale, as seen in section 4.