 |
The third major area to be parallelised was the Collocate (calculate_rho_elec) and Integrate (integrate_v_rspace) routines. These take a list of Gaussians (products of atom-centred Gaussian basis functions) and map these to regular grids, prior to Fourier Transformation, and vice versa. Again, see [1] for how this step makes up a key part of the Quickstep dual-basis algorithm.
Taking the collocate case as an example, the input to the routine is a list of 'tasks' which correspond to the gaussians to be mapped. These tasks are represented as large integers, which encode (among other things) the IDs of the relevant atoms, and the grid level to which the task is to be mapped. The atomic IDs are used to index into the density matrix deltap to retrieve the coefficients of the associated primitive Gaussian functions. The product is then calculated and is summed onto the assigned grid level. Integration is precisely the reverse - for each task, a region of the grid is read, and this data is then stored in the relevant location in the matrix (specified by the task parameters).
Although similar, both of these procedures present different challenges to efficient OpenMP parallelisation. For collocation, the matrix is read-only, so can be shared by all threads, but the grids are writable, and moreover, in general the Gaussian products may overlap on a given grid level so we need to ensure that writes to the grids from multiple threads are summed correctly, rather than allowing a data race condition to occur. For integration, the grids are read-only, but this time the matrix must be protected so that a single block of the matrix is only updated by a single thread. The matrix is in fact stored in DBCSR format, which makes provision for threading by allowing each thread to update a `work matrix' - a working copy of the matrix. Additions or modifications to the work matrix are combined in a process called `finalization'. For correct finalization, each work matrix should contain a different subset of blocks of the whole matrix, so we require that each thread only works on tasks corresponding to a particular atom pair before the matrix is finalized.
Most of the difficulties can be overcome by pre-processing the task list at the time it is created to determine the indices at which the tasks for each grid level and each atom pair start and end (the list is already sorted in this order). Thus we can transform the existing loop:
DO ipair = 1, SIZE(task_list} <process each task> END DO
into a parallel loop:
DO ilevel = 1, ngrid_levels
!$omp parallel do
DO ipair = 1, task_list%npairs(ilevel)
DO itask = task_list%taskstart(ilevel,ipair), task_list%taskstop(ilevel,ipair)
<process each task>
END DO
END DO
!$omp end do
END DO
This preserves the high-level ordering of the tasks (by grid level) which retains the benefit of keeping only one grid level (which could be several megabytes in size) in cache at any given time.
To correctly perform the integration, we need to add the creation of work matrices at the start of each ilevel loop, and finalize the matrix at the end of each loop. Thus the threads can partition the loop over atom pairs arbitrarily at each grid level (and the number of tasks per pair can vary over the grid levels), while maintaining the condition that each matrix block is only updated by a single thread before each finalization.
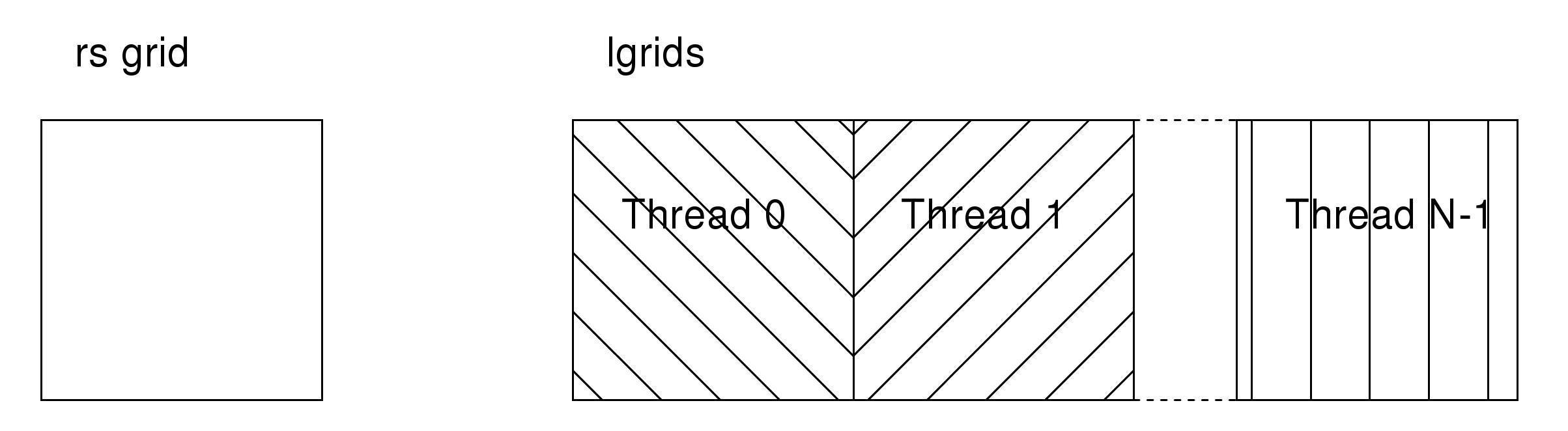
For collocation, the situation is slightly more complicated, due to the fact that we need to be able to sum data onto potentially overlapping regions of the grids. This is solved by allocating a copy of the grid for each thread (local grids or lgrids in the code), and then performing a reduction in parallel at the end of each ilevel loop. During each loop, a thread writes the data corresponding to its set of tasks to a private region of the lgrids (figure 5).
 |
At the end of the loop, the grids are reduced in parallel back onto the original realspace grid. Two methods were implemented for this reduction. In the first method, each thread sums the contributions from each threads lgrid back into a single region of the rsgrid (figure 6).
This has the advantage that every thread can operate without synchronisation since it writes to a disjoint part of the grid. However, it has to read from data that was previously written by other threads, which can be relatively costly as this data may be in cache on another core. Because of this, a second method was implemented which performs somewhat better. In this case (figure 7) each thread sums a region of its lgrid into the rsgrid. The regions are distributed cyclically, so at each step, only a single thread writes to a given region of the rsgrid. Synchronisation is required between each step, but this cost is outweighed by the benefit of a reduced number of reads of remote data, and so this method was implemented in the current CVS version of CP2K.
It is not possible to benchmark the collocate and integrate routines directly as for the FFT and RS2PW, however it is easy to extract the time spent in these routines from short runs of a whole-code benchark H20-64. This is a short molecular dynamics run with 64 water molecules is a 12 Åcubic unit cell (as used in the previous dCSE project [1]). The results of running on 36 nodes of HECToR Phase 2b with a single MPI task per node and a varying numbers of OpenMP threads are shown in table 1. The table shows that integration scales well as the number of threads is increased since the memory heirarchy is used effectively and there is little data sharing except at the matrix finalizatio, which only occurs once per grid level. However, with collocation, due to the expensive grid reduction step, speedup is only achieved up to 6 cores (a single processor) due to the aforementioned costs of remote memory access and synchronisation. It may be possible to replace this scheme with a tree-based algorithm, aiming to reduce the number of copies from one processors memory bank to anothers, but this was not investigated within the time available for the project.