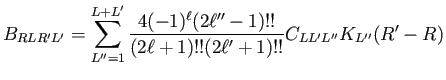Electrostatics

The electrostatic potential is parametrised with respect to $\Delta_{\ell\ell'\ell''}$ parameters which we shall call polarisabilities.

Firstly a matrix with structure dependent constants and one with their radial derivatives (if the calculation of pressure is required), are built before the start of the self-consistency loop:

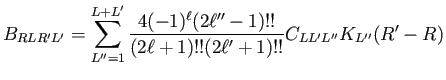$$B_{RLR'L'} = \sum_{L''=1}^{L+L'}{ \frac{4 (-1)^{\ell} (2\ell''-1)!!}{(2\ell+1)!!(2\ell'+1)!!} C_{LL'L''} K_{L''}(R'-R)}$$ (10)

The Gaunt coefficients:

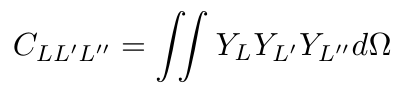$$C_{LL'L''} = \iint Y_{L}Y_{L'}Y_{L''} d\Omega$$ (11)

are precalculated in the beginning and reused. The Hankel functions

$$\qquad K_L(r) = r^ {-\ell-1}Y_L(r)$$ (12)

are the actual structure dependent factors. During the self-consistency the charge multipoles $Q$ are calculated on every step:

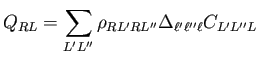$$Q_{RL} = \sum_{L'L''}\rho_{RL'RL''} \Delta_{\ell'\ell''\ell} C_{L'L''L}$$ (13)

The components of the potential in a spherical wave expansion are a straightforward product of the structure matrix and the multipole block vector:

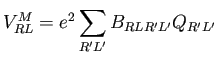$$V^M_{RL} = e^2 \sum_{R'L'} B_{RLR'L'} Q_{R'L'}$$ (14)

and the update to the Hamiltonian onsite elements and the contribution to the energy are:

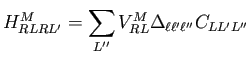$$H^M_{RLRL'} = \sum_{L''} V^M_{RL} \Delta_{\ell\ell'\ell''} C_{LL'L''}$$ (15)

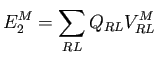$$E^M_2 = \sum_{RL} Q_{RL} V^M_{RL}$$ (16)

$L+1$ in $B$ is required for accurate calculation of the forces and this tends to increase its size very significantly for $d$ elements. The forces due to the Madelung terms are:

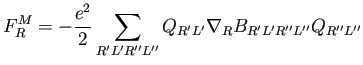$$F^M_R = - \frac{e^2}{2} \sum_{R'L'R''L''} Q_{R'L'} \nabla_R B_{R'L'R''L''} Q_{R''L''}$$ (17)

A complication arises however in the nonorthogonal case due to offsite contributions:

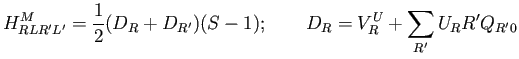$$H^M_{RLR'L'} = \frac{1}{2} (D_R + D_{R'}) (S - 1); \qquad D_R = V^U_R + \sum_{R'}U_RR'Q_{R'0}$$ (18)

And additional forces:

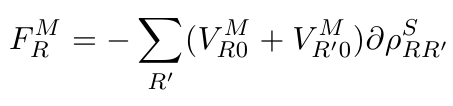$$F^M_R = -\sum_{R'} (V^M_{R0} + V^M_{R'0}) \partial \rho^S_{RR'}$$ (19)

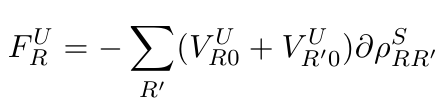$$F^U_R = -\sum_{R'} (V^U_{R0} + V^U_{R'0}) \partial \rho^S_{RR'}$$ (20)

The quantity $\partial \rho^S_{RR'}$ needs to be calculated in every iteration:

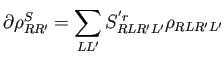$$\partial \rho^S_{RR'} = \sum_{LL'} S^{'r}_{RLR'L'} \rho_{RLR'L'}$$ (21)