Practical implementation

Starting from a given set of parameters the $H$ and $S$ matrices are built. The objective is then to solve the nonlinear problem of finding a charge distribution consistent with the induced potential. This process consists of iteratively recalculating the charge shifts

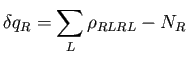$$\delta q_R = \sum_L\rho_{RLRL} - N_R$$ (3)

and the resulting update to the Hamiltonian matrix:

$$H = H^0 + V_U + V_{xc}; \qquad V^U_R = U_R \delta q_R; \qquad$$ (4)

There are aditional terms originating from the electrostatics and spin polarisation which shall be expanded upon later.

Generally, either the potential or the density or charges are mixed with certain amounts of previous values to avoid instability and accelerate convergence. The mixing is a very complex problem on its own and shall not be addressed further here. The traditional approach to calculate the charges from H is by solving the secular equations in matrix form:

$$HZ = SZ\Lambda$$ (5)

through diagonalisation. Here $Z$ is the matrix containing the eigenvectors of $H$ in its columns and $\Lambda$ is a diagonal matrix holding the respective eigenvalues. A Fermi level $\varepsilon_f$ and occupancy function $f(\varepsilon)$ is then found such that its integral is the total number of electrons in the system. The diagonal matrix $f$ is the matrix representation of the occupancy in the basis of $Z$. The representation in basis of the implicit local atomic basis functions $\rho$ is calculated, using the overlap condition $ZZ^* = S^{-1}$, by:

$$\rho = SZfZ^{-1} = SZf(SZ)^* = SZfZ^*S$$ (6)

or

$$(S^{-1}\rho) = ZfZ^*S$$ (7)

The occupancy at 0K is a step function equal to 2 for an occupied state and 0 for unoccupied. If uncoupled spin polarisation is also allowed then the occupancy of each spin orbital, (restricted to up and down only) is 1 and 0 respectively. If there are states very close to, or on the discontinuity, smearing may be applied to avoid problems. This yields an entropic contribution to the energy corresponding to the temperature of the smearing.

The density which is calculated separately for different spins is called spin density, and the difference between the two spin densities gives the magnetic moment $m$ of the system:

$$m = \rho_{\uparrow} - \rho_{\downarrow}$$ (8)

the magnetic moment induces a potential to be added to the Hamiltonian

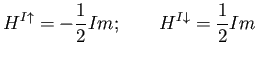$$H^{I\uparrow} = - \frac{1}{2} I m; \qquad H^{I\downarrow} = \frac{1}{2} I m$$ (9)

the Stoner $I$ is a model parameter. Since spins are uncoupled there are actually two separate Hamiltonians and subsequent quantities must be treated independently. If there is a coupling through additional parameters then the basis functions double in number simply creating larger matrices. Detailed derivation is provided in [4].