Density matrix from eigenvectors and occupancies

The density matrix has a fundamental place in the derivation of the nearly all other properties of interest as shown in section 1.2.2. In the original implementation however, the band/state index in the outermost summation results in a repeated recalculation of quantities which require regular updates to wide areas of memory for the charges array, the site energies and forces. Issues were severely complicated by the presence of a non unit overlap matrix.

There is an elegant and efficient way to obtain the full $\rho$ for a positive occupancy function e.g. as in Methfessell-Paxton[6] with N=0, or a plain step function. Each occupied state's eigenvector can be scaled efficiently by the square root of the occupancy function then the array containing all occupied eigenvectors may be transposed. Then an equivalent of dgemm('t','n', .., .., nstates, 1.0d0, $\tilde{Z}$, .., $\tilde{Z}$,...) will access elements sequentially and will be efficient in obtaining $\rho$. The positive occupancy requirement can be relaxed when the eigenvectors are complex (i.e. not at the $\Gamma$ point).

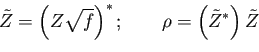$$\tilde Z = \left(Z \sqrt f\right)^*; \qquad \rho = \left(\tilde Z^*\right) \tilde Z$$ (28)

A second conclusion from section 1.2.2 is that the full density matrix is not actually needed. For all listed properties of interest it will suffice to know of only the blocks matching a corresponding nonzero Hamiltonian block. Fortunately the Hamiltonian (and overlap) matrix in TB is fairly sparse, often no more than 10% filling²which decreases with system size. Furthermore the density matrix blocks required need not be saved, except for the diagonal ones necessary for the electrostatics. They can be used on the spot to accumulate a local contribution to the quantities of interest which are only diagonal, and then overwritten on the loop for the next atom. This leads to a walk over the atoms and their neighbours, performing a dot product between block columns of $\tilde{Z}$, the effort for which scales linearly with the number of atoms since the hoppings are short ranged. Additionally if the site energies and forces are not strictly required during self-consistency, the diagonal density matrix blocks will suffice further and reduce the effort by a factor equal to the average number of neighbours per atom. Since a block may be dimensioned anywhere from 1 to 9 by 1 to 9, the dot product is performed by either the _dot/c, _gemv or _gemm routine, depending on the case.

Separate versions for real and complex handling were originally written. Since this was mostly a duplication, one approach would be to use the preprocessor to produce two object files from one source (as done in the ScaLAPACK diagonalisation tester) but a more convenient solution was to use the real(8) type and then add an extra index of passed size on the left side of the arrays, which is either 1 for the real case or 2 for the complex. Then procedure pointers dot, gemv and gemm are associated with the appropriate `d' or `z' version. Since dot is a function which returns the result in a register, a generic subroutine was defined to work around Fortran's strong typing and type compatibility rules. The overhead of dealing with the extra index and function pointers is not significant and in the author's opinion this solution provides better maintainability. However, since an assumption is made about the storage of the complex type there may be problems with platforms which do not follow this.