dCSE project report
Combined-Multicore Parallelism for the UK
electron-atom scattering Inner Region R-matrix codes on HECToR
C J Noble1, A G Sunderland2
and M Plummer3
(1CJN,
2AGS, 3MP)
Department
of Computational Science and Engineering, STFC Daresbury
Laboratory, Warrington WA4 4AD, UK
ABSTRACT: Electron collisions
with atoms were among the earliest problems studied using quantum mechanics.
However, the accurate computation of much of the data required in astrophysics,
plasma and optical physics still presents huge computational challenges, even
on the latest generation of high-performance computer architectures, such as
the Cray XE series. A suite of programs based on the ‘R-matrix’ ab initio approach to variational solution of the
many-electron Schrodinger equation has been developed and has enabled much
accurate scattering data to be produced. However, current and future
calculations will require substantial increases in both the numbers of channels
and scattering energies involved. An earlier dCSE report
concentrated on optimization of PFARM (http://www.hector.ac.uk/cse/distributedcse/reports/prmat/), the program suite’s
high-scaling energy-dependent ‘outer region’ code. We now address the
scattering energy independent ‘inner region’ in which intricate configuration
interaction Hamiltonian and multipole matrices for
the many-electron system are constructed (and diagonalized).
Radial integrals and angular couplings are calculate separately then combined
together. Serial, and in certain cases OpenMP-paralellized
codes, have been extended to full many-node parallelism using a mixture of (a)
mixed-mode MPI plus OpenMP techniques, and (b) pure
MPI with intra-node shared memory segments and object-oriented Fortran 2003.
Both methods take full advantage of the multicore nature of modern
architectures. The three ‘construction’ codes now scale across multiple HECToR nodes. We have also developed two utility packages
in object-oriented Fortran 2003: a shared memory segment package (with
associated semaphores, intra- and inter- (virtual) node communicators etc) and
a parallel I/O package adapted using asynchronous MPI-IO from an existing
serial double-buffered direct access package: this allows independent parallel
reading and writing combined with straightforward access to non-contiguous
selections from large amounts of stored data. These utility packages are of
course particularly suited to the R-matrix codes but are also of general
interest.
KEYWORDS:
atomic physics, electron-atom scattering, R-matrix, configuration interaction,
spherical tensor algebra, surfacing coefficients, Hamiltonian matrices,
parallel computing, multicore systems, mixed-mode, shared memory segments,
asynchronous parallel I/O, passive one-sided communication, object-oriented
Fortran 2003, CCPForge.
2. dCSE personnel,
objectives and outcomes.
1. Introduction
Electron-atom (ion) scattering
data are essential in the analysis of important physical phenomena in many
scientific and technological areas. These include the understanding of
atmospheric processes, diagnostics of impurities in fusion plasmas (including
JET and the new ITER project), interpretation of astrophysical data, the
development of environmentally safer alternatives to replace mercury vapour
lighting and investigations of laser-produced plasmas (such as for
next-generation nanolithography tools). In addition, the HiPER
project (http://www.hiper-laser.org) for laser-ignited fusion, with
associated experiments in laboratory astrophysics, opacity measurements, laser-excited
hollow atoms and atoms in strong magnetic fields will stimulate detailed
calculations of atomic scattering data. Despite the importance of these
applications little accurate collision (theoretical or experimental) data is
available for many complex atoms and ions. Also of current (global) interest
are electron-atom (ion) interactions in laser fields: multiphoton
ionization, high intensity ultrafast processes followed by field-assisted
recombination and scattering, harmonic generation and coherent control. In the
UK, ab initio code to treat these laser field
processes for atoms and molecules is being developed by, for example, the
UK-RAMP consortium, supported by Collaborative Computational Project CCPQ
(formerly CCP2) [1].
PRMAT [2] is a suite of programs
based on the ‘R-matrix’ ab initio approach to variational solution of the many-electron Schrödinger
equation for electron-atom and electron-ion scattering [3]. Relativistic
extensions have been developed and the codes have enabled much accurate
scattering data to be produced. The package has been used to calculate electron
collision data for astrophysical applications (such as: the interstellar
medium, planetary atmospheres) with, for example, various ions of Fe and Ni and
neutral O, plus other applications such as plasma modelling and fusion reactor
impurities (for example ions of Sn, Co, and in
progress, W). In R-matrix calculations configuration space is divided into two
regions by a sphere centred on and containing the atomic or molecular ‘target’.
Inside the sphere an all-electron configuration interaction (CI) calculation is
performed to construct and diagonalize the full
(energy-independent) Hamiltonian for each scattering symmetry within the finite
volume in readiness for energy-dependent ‘R-matrices’ to be constructed on the
boundary. The massively parallel outer region code PFARM was the subject of an
earlier dCSE project [4]. The current project is
focussed on the inner region codes, specifically the non-relativistic inner
region codes comprising 3 or 4 standalone modules as shown below. The codes are
used on HECToR by UK-RAMP and the ‘Atoms for
Astrophysics’ project in particular.
Figure 1. Program flow
for the
inner region codes:
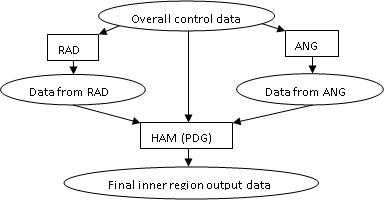
The RAD module calculates 1- and
2-electron direct and exchange radial Hamiltonian integrals plus multipole integrals for all the radial bound and continuum
orbitals involved in the calculation: if the whole system comprises N+1 electrons
(N-electron targets) then the wavefunctions will
include antisymmetrized coupled products of N ‘bound’
orbitals (including ‘pseudo-orbitals’) and 1 continuum orbital, plus certain antisymmetrized coupled products of N+1 bound orbitals: the
continuum orbitals do not vanish at the sphere boundary radius. The ANG module
calculates angular couplings for the diverse open- and closed-channel CI target
state plus continuum orbital combinations and the ‘N+1’ product couplings: this
is the most complicated module and a more detailed description is given in
section 4. HAM essentially gathers together the diverse radial integrals and
angular couplings required for each non-relativistic ‘LSπ’ (orbital and
spin angular momentum, parity) scattering symmetry to form the N-electron
target states and the N+1-electron scattering Hamiltonian matrices, plus
N-electron multipole and, if required, N+1-electron
dipole matrix elements. The Hamiltonians are then diagonalized
and the eigenvalues, eigenvector boundary amplitudes and associated dipole
matrices are output, either to the PFARM (or serial FARM [5]) code or to codes
which modify and recouple the output for relativistic (‘Jπ’) calculations,
or to the UK-RAMP multiphoton codes.
At the start of the project the
package had become separated into two or three effective packages. For
scattering calculations, radial continuum functions, orthogonal to the input
bound orbitals, with fixed sphere radius boundary conditions were generated on
a numerical grid (the ‘traditional’ method [2, 3]). RAD, ANG and HAM were
serial codes (ANG included some OpenMP directives).
The diagonalization was either performed serially
with Lapack inside HAM, or for complex atoms with
open d-shells a separate program PDG read output from HAM and performed it
using ScaLapack. The N+1-electron dipole matrices
were not required. For the UK-RAMP multiphoton codes,
the RAD, ANG and HAM codes were needed to generate ‘start-up’ data for the TDRM
[6] and RMT [7] laser-atom codes. The full dipole matrices were required. The
radial continuum orbitals were generated from sets of B-splines, with the knot
points chosen to form an appropriate radial grid. These functions obey
arbitrary boundary conditions at the boundary radius, allowing the multiphoton calculation to proceed without certain
disruptive (in this case) correcting factors [3] needed for the fixed boundary
condition functions. In general ~100 (up to 200) B-splines are needed for each
orbital angular momentum l (B-spline
expansions are also used to fit to the input bound orbitals), compared to, say,
20 or 30 traditional continuum orbitals for each l. This RAD code was parallelized with OpenMP
by H van der Hart (Queen’s University Belfast), while HAM was purely serial:
the ‘targets’ treated so far in this context are relatively less complex with
open p-shells.
It was desired by the user
communities to bring the packages back together as a single package maintained
on CCPForge [8], so that future optimization and extensions
would apply across the scientific applications. It was also desired to extend
the RAD parallelization, parallelize HAM to allow for more ambitious
calculations (both for complex atoms and for future applications and extensions
for which the fixed boundary condition basis would be troublesome), and most
importantly, parallelize the ANG code as this was becoming a major bottleneck
for complex calculations despite a highly sophisticated procedure for dealing
with the spherical tensor algebra [9].
2.
dCSE personnel, objectives and outcomes.
The original application, sent in
by the authors with backing from Dr M P Scott and Professor H V van der Hart of
Queen’s University Belfast, asked for 18 months of effort shared between AGS
and CJN for an ambitious plan to achieve the above aims and to explore new
coding that would make full use of the XE6 32-multicore many-node HECToR architecture (and hence comparable and future
multicore HPC systems, also local multicore few-node systems). The plan was to
explore both mixed-mode OpenMP/MPI coding and the use
of IPC shared memory segments to utilize the multicore structure in a pure MPI
context. The parallelization also implied use of parallel I/O between the
internal region codes, with more standard/portable final output. Since the ANG code is the most mathematically
complex, requiring an expert in theoretical atomic physics (and many-electron
angular couplings) as well as in numerical analysis and HPC, this would be handled
by CJN, employing Fortran 2003 objects and structures to simplify the relation
between the high-level coding and the theory while maintain high performance
and future-proofing the code (as in his contribution to the previous dCSE project [4]).
AGS would handle RAD developments, while HAM developments would be
shared. The project was awarded 12 months’ effort with instructions to attempt
the full plan. Owing to commitments to the expanding PRACE [10] network, the
final effort breakdown was around 0.7 (CJN) to 0.3 (AGS) and CJN has handled both
ANG and the main development of HAM. Due to complications with compilers and
other matters to be described below, a further concession was that during the
project, the intra-node parallelization of RAD would be via OpenMP
and that of ANG and subsequently HAM via MPI with shared memory segments.
Summary outcomes are given here with more details and performance data in the
following sections.
RAD objectives:
1.
Combine the B-spline and ‘traditional’
continuum function generation with a single interface to produce a single RAD
code for all applications.
2.
Extend the OpenMP
multicore parallelism to the bound orbitals and the general scheme to the
‘traditional’ continuum functions. Provide an option to use System V shared
memory and pure MPI. (The OpenMP-produced data will
produce results that can be used to assess the accuracy and performance of the
System V MPI implementation).
3.
Introduce a higher level task-management
parallelism and MPI communicators over the l
variables (for generation and integral combinations) and distinct bound or open
(continuum) sections, with associated memory distribution. Use the ‘xstream’ parallel I/O library to keep track of parallel
data and to write final data.
Objective 1 has been completed:
RAD is now a single code with options for traditional and B-spline orbitals.
The OpenMP code in objective 2 has been made more
efficient as will be seen in the next section. This effort was concentrated on
the B-spline code as for all the test cases so far the traditional RAD code
takes much less time to run, the B-spline code having more ‘orbitals’ and
‘grid’ points, but it has also improved calculation of the traditional
integrals. The ‘shm’ shared memory segment module
developed for ANG was tested and verified independently (section 4). Since the
application of OpenMP in RAD is computationally
fairly straightforward and efficient, based on parallelizing certain important
inner loops in both construction of orbitals and in subsequently performing the
integrals (thus relatively few ‘threadprivate’
variables are needed in the Fortran 95 module-based
code), replacing OpenMP with the shm
module remains an option but was not prioritized.
The MPI introduction in objective
3 has been completed by distributing work over outer loops in the two halves of
the code: the loops are essentially orbital indices {n, l expansion label and
angular momentum} in the first half, and loops over 4 sets of orbital indices
in the second half. This was not trivial as the orbitals generated in the first
half of RAD are required by all loops in the second half which performs the
integrals, thus some broadcasting is required. In fact, intermediate ‘legacy’
files storing the orbitals have been removed as modern systems have more than
enough memory to cope with the data: using ‘shm’ to
store this data is obvious follow-up
work, to cope with future extremely large orbital bases. At the close of the
project, the final output from RAD is being upgraded to allow data to be
written using the new ‘pfilehand’ module developed
for ANG (as part of CJN’s ‘xstream’ package of custom
I/O modules, see [4]).
ANG objectives:
1.
Modification of the OpenMP
code to improve scaling and performance, ideally simplifying the ‘threadprivate’
and binding requirements, with rigorous testing of the (relatively complex) OpenMP structure to ensure strict compliance with OpenMP rules on HECToR. Incorporate the parallel ‘xstream’
I/O library to keep track of written data.
2.
Incorporate the SMP parallelism into
other sections of the code. Reproduce the parallelism using the System V
module.
3.
Introduce overseeing task-management MPI
communicators into the outer loops over basic symmetries and ‘open’ and
‘closed’ sections of the code, with associated memory distribution.
4.
At all stages, carefully comment and
annotate the code. Give clear descriptions of the modular (and sub-modular)
structure. While this will not directly contribute to output from performance
benchmarks, it is essential for the long life and future enhancement of the
code, and for the planned post-project) official CPC write-up (and hence
enhanced user base). The availability of the code will be as for RAD, on the
4.5 (9 real) months timescale, with the code to be available on CCPForge.
The ANG code at the start of the
project included OpenMP directives in the two places
identified as needing parallelism: the initial construction of ‘surfacing
coefficients’ and the subsequent ‘bound-bound’ coupling evaluation (these terms
are explained in the detailed description in section 4) and had worked
reasonably well in few-thread parallel on the IBM Power-series HPCx service
(giving correct results). However on HECToR the code
as written either failed to run or gave obviously incorrect results on all the
compilers with OpenMP switched on. Race conditions
were causing severe problems and examination of the code showed that the OpenMP was not strictly correct and standards-conforming:
the IBM implementation was compensating for the errors. Some time was spent at
the start of the project correcting more obvious errors, but the combination of
Fortran 95 code structure, many ‘threadprivate’
variables and large numbers of out-of-scope variables made analysis difficult:
the parallelism required for the code is coarse-grained over high level loops
calling many subroutines. Owing to CJN’s personal situation (he is retired and
freelance, working from New Zealand and unable to travel, with HECToR access fast enough to work but not fast enough to
allow full remote use of TotalView and similar
tools), it was decided to suspend work on the OpenMP
code and concentrate on MPI and shm. It is likely that a tool such as Intel
Parallel Inspector [11] would be able to shed light on this problem and this
remains as follow-up work for DL staff. However a practical reason for concentrating
on the MPI approach is that many current and most envisaged calculations will
certainly require more than one node to run in an acceptable time on
batch-queue resourced systems such as HECToR.
The MPI/shm
approach has turned out to be a great success and the new ANG code and the two
utility packages shm and pfilehand
will, we hope, turn out to be lasting legacies of this project. The shm package was developed to allow each shared memory
segment to be a Fortran 2003 object accessed via
pointer components. The package is described in more detail in section 4 and
includes appropriate semaphores, barriers and routines to attach and detach
from the segments. The iso_c_binding components and
associated C routines are at a low level within the package so external access
is kept to strict Fortran. This access is particularly
appropriate for ANG and the Fortran 2003 shm package is complementary to the MPI-1 and Fortran-95
compatible modules previously developed for HECToR
and the CASTEP code [12]: an academic paper describing the two modules and
their performance is in preparation. In ANG, shm is
used to store tables of ‘surfacing coefficients’ calculated in parallel
(section 4).
‘pfilehand’ is a double-buffered parallel I/O module
using asynchronous MPI-IO calls with indexing records reserved for minimal
information for locating bulk data and allowing subsequent parallel reading to
be completely independent of the communicators used to perform the parallel
writing. It is again accessed as Fortran 2003 objects
and is used in the main ANG code to write the final data which is calculated in
parallel using MPI: this parallelism has been extended to all the various ANG
routines, though the bound-bound coupling remains the most time-consuming. The pfilehand module was developed from an older set of serial filehand routines for direct access files used throughout
the R-matrix codes and is therefore particularly suited to these codes (and
others which use serial filehand). However, pfilehand is relatively easy to use and should be of
general interest, competitive with more general packages. It is used in ANG in
combination with parallelized outer loops over coupling indices to calculate
the required couplings from the surfacing coefficients. The new parallel ANG code
has been tested for scaling up to 256 cores so far, from an initial serial
code, and the shm and pfilehand
modules are available as standalone packages with test runs. They are being
made available on CCPforge [8] and we aim to publish
them.
We note that the Fortran 2003 code requires a standards-conforming Fortran
2003 compiler. The Nag 5.3.rc5 compiler has the functionality required, as does
the recent IBM compiler xlf13 (as tested on a Power7 machine). Tests of the
packages have shown up bugs in the pgi compiler which
are being fixed piecemeal with ongoing releases, and in the Cray compiler. Cray
have requested and received a ‘beta’ version of the ANG code to use as part of
their validation test suite for compiler upgrades. We thank the HECToR helpdesk for facilitating access to the compiler
experts. We await the Cray Fortran 2003 compiler in
particular, as our tests confirm that this is the best-performing compiler for
the serial versions of the PRMAT codes and the parallel RAD code on HECToR. The ANG code is carefully commented and detailed
notes link the routines to the main theory [9]. These will be supplemented by
the planned publication document. The availability time for the code was
underestimated for the reasons described here, however
it is now available for users and feedback.
HAM objectives:
1.
MPI sub-task communicators looping over LSπ scattering symmetries and
classification of matrix elements (open-open, open-closed and closed-closed,
both Hamiltonian and dipole elements). Arrange Hamiltonian output data files
sympathetically to be picked up in parallel by PDG. Distribute the dipole data
for different symmetry combinations.
2.
Introduce OpenMP/System
V parallelism into the construction of the matrix elements.
3.
Adapt the routines for recalculating the
dipole matrices (from the eigenvector coefficients after Hamiltonian diagonalization) and other eigenfunction
data for the field-atom work so’ that they appear as an option in the parallel
PDG code.
Parallel
loops have been introduced over the matrix element formation routines, with pfilehand used to pick up ANG data (and RAD data as an
option), with shm introduced and used where needed.
The ‘xstream’ routines developed as part of the
previous dCSE have been introduced in the handling of
the final data so that ‘traditional’ binary output or PFARM- and PDG-preferred
XDR output may be chosen automatically. The HAM code is now a single parallel
code for both scattering and multiphoton
applications. At the time of writing, the code is undergoing an extremely
thorough set of validation tests, which we considered to be of primary
importance so that the parallel code could be delivered to users. We will
update this report with full scaling data once these tests have been completed.
The final work on the dipole matrix elements, replicating HAM routines for
post-diagonalization treatment explicitly in PDG,
will be performed subsequently as an upgrade to the released code.
3.
Detail: RAD
In this section we show some
performance results for the modifications made to RAD. We first consider the OpenMP code. Our main modification was to re-order loops in
the second half of the code that calculate 2-electron exchange integrals over
four orbitals and an inter-electronic potential term {r<k/r>(k+1)}
(r< is the lesser or r1 and r2). The
algorithmic set-up of the code is such that where possible the inner integral
is stored for a particular combination of orbitals to avoid recalculation,
however the orbital index ordering for the exchange integrals ran counter to
this and much unnecessary recalculation was being done. The loop reordering was
performed while maintaining the ‘correct’ expected ordering for the writing to
the output files. In addition, the integrals were in many cases written
individually to the serial filehand output buffers:
while the buffering mechanism in filehand compensated
to a reasonable extent, this has been rearranged so that filehand
routines can be called less frequently for arrays of integrals. We also
collapsed some inner loops and put in an option to move the OpenMP
loop up one level, hopefully to reduce OpenMP
overheads. Results are shown for an oxygen test case using 180 B-spline
functions per angular momentum. We compare original and revised code execution
time for up to 32 threads using gnu, pgi and cray compilers (at –O3 level, -fast for pgi).
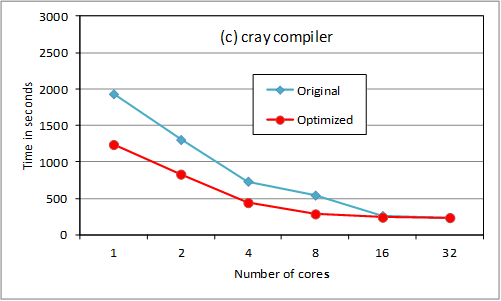
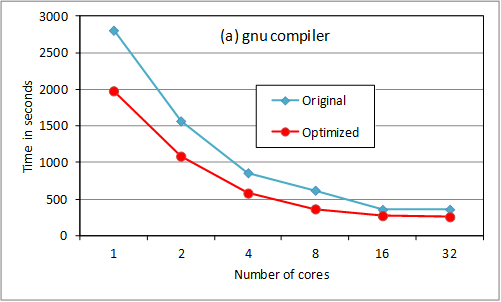
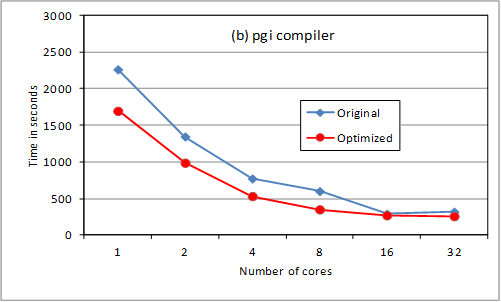
Figure
2. RAD OpenMP tests.
The loop reordering provides
substantial serial optimization. Above 8 cores, the storage option slows down
the scaling. We are checking returning the OpenMP loop
to its previous position for 16 and 32 cores (ie so
that less data needs to be held in memory). The cray
compiler is much better suited to HECToR
for this code, though this may not be the case on other platforms. Note that
all tests were performed on a full node (ie the
few-thread runs had access to all the memory on the node if required,
etc).
The results above include the
writing (and re-reading) of sets of orbitals to temporary files. This approach
has traditionally been used in the serial code in order to minimize memory
overheads on former memory-limited architectures. However, the latest HPC
architectures such as Hector, provide relatively
generous memory provisions (32GB) per node, and therefore this out-of-core
storage approach has been replaced with on-core (memory) storage in the new
parallel code.
We now consider
preliminary results (for the optimized code) using the cray
compiler following the introduction of the MPI communications. The main code
developments for implementing this new level of parallelization in RAD involves
(i)
distributing input configurations to all MPI Tasks at the start of the run, (ii) the replacement of temporary files
with memory-based storage and (iii) a
distribution of outer loop angular momentum l
values amongst MPI tasks for both basis function and radial integral
calculations. Note that this option not only allows for use of more than one
node, but also can improve overall performance by determining optimal MPI task/
OpenMP thread combinations within a node.
The figure shows three cases, the
pure OpenMP results for {8, 16, 32} threads already
shown above, results for 8 OpenMP threads each for
{1, 2, 4, 8, 16} MPI tasks (ie {1, 1, 1, 2, 4}
nodes), and results for 16 OpenMP threads each for
{2, 4, 8} MPI tasks (ie {1, 2, 4} nodes).
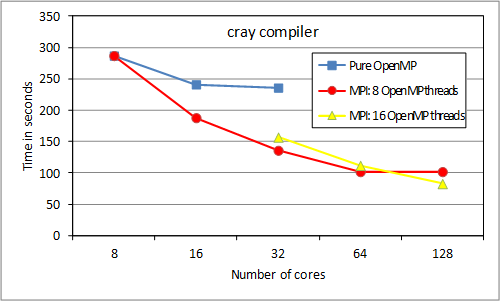
Figure
3.
RAD mixed-mode tests.
It may be seen that for this
oxygen test, the intermediate writing to disk did not significantly hold up
performance (or its removal has compensated for any (minimal) overhead for 1
task introduced by the MPI code). The introduction of the MPI tasks,
complementary to the OpenMP parallelization, has
significantly improved the overall performance within one node, and the
performance scales acceptably to two nodes.
The lack of scaling between 2 and
4 nodes for 8 threads per task may be explained as due to the test case: the
outer loop parallelized with MPI has 8 independent (after appropriate
preliminary data transfer) iterations. Thus we now show multi-node results for
an expanded case (more realistic) with 16 independent outer loop iterations
(note the linear horizontal scale for this figure). We have {4, 8, 12, 16} and
{2, 4, 6, 8} MPI tasks respectively.
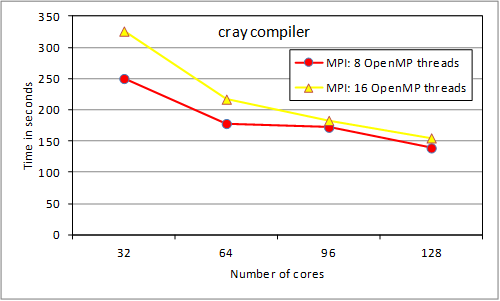
Figure 4. RAD mixed-mode
tests (16 iter.)
While the 4-node run is now
faster than the 2-node run, load-balancing of tasks to iterations is affecting
the scaling. The iterations were assigned to tasks in round-robin fashion and
while the overall time to completion was stable for repeated testing, the
load-balancing between threads became progressively worse: from about 10% difference for 2 tasks, to some tasks taking nearly twice as
long as others for 16 tasks. These timing differences reflect the different
computational loads associated with different l values assigned to the different MPI tasks.
This
load-balancing issue can be compensated for, for instance by a more careful
allocation of tasks to particular loops by a code author (who can tell which
loops are likely to be busier). We note that ~0.8 of the execution time is
taken up by the second, integral evaluation, stage. Now that the MPI procedure
is in place it is straightforward to collapse the two outer loops and assign
the resulting single loop to MPI tasks, which will improve scaling for more
than 2 nodes by statistical smoothing. The updated report will show improved
timings. We will also introduce the passive RMA ‘sgc’
scaleable global counter (already part of pfilehand, see section 4) to balance out the work among
tasks: RAD provides a useful comparison test for the two approaches (section
6). As things stand, the performance and scalability of RAD has been
substantially improved, the use of MPI allowing the OpenMP
operations to be performed with the optimum number of threads, usually 8 on HECToR.
4.
Detail: ANG
In this section we give more
substantial detail on the background to the code and the new packages,
finishing with some performance figures.
4.1: Background
The R-matrix formalism ([3] and
references) was developed by Wigner and Eisenbud to
treat proton and neutron collisions with nuclei. The idea was to treat these
nuclear collisions as two separate collision problems according to whether the
incident nucleon was external to the target nucleus and Coulomb forces mediated
the interaction between the colliding particles or the incident nucleon was
inside the target and the interaction was via short-range nuclear forces.
Matching the inverse logarithmic derivatives of these two solutions at the
boundary of the target nucleus produces a real matrix, the R-matrix, which can
be used to compute cross sections, resonance parameters and other physical
observables.
In the 1970s P G Burke extended
this formalism to treat electron-atom collisions. In atomic systems the
requirements of the Pauli exclusion principle dictate
that if the incident electron is inside the charge cloud of the target atom or
ion exchange effects are important and result in a complicated set of integro-differential equations describing the collision
process. If, however, the incident electron is outside the charge cloud of the
target a simpler non-exchange scattering problem must be solved. The adapted
R-matrix formalism simplifies the computation necessary to treat the collision
from first principles.
Following an initial (and widely
used) package RMATRIX-1 [13] developed at Queen’s University, Belfast, the
RMATRX-II formalism was developed by P G Burke, V M Burke (of DL) and K M Dunseath ([9], referred to hence as BBD) to improve the
efficiency of previous implementations of atomic R-matrix theory in order to
tackle more complex electron configurations. As larger and more complex atomic
systems were considered the limitations of the initial code had become
apparent. In particular the calculation of the angular integrals necessary to
derive Hamiltonian matrix elements became a computational bottleneck as the
contribution of more deeply bound electron shells was considered. The number of
configurations rises steeply as more shells are unfrozen and allowed to
participate in the collision process. BBD published an improved algorithm for
treating atomic collision in which a set of angular momentum transformation
coefficients, termed surfacing coefficients, are derived that express the
recoupling transformation of a pair of electrons in the target occupied shells
to the top of the coupling tree where it may interact via the one- and
two-electron integrals involved in the interaction. These coefficients involve
fractional parentage coefficients (to allow for electron shell antisymmetry), Racah coefficients
and kinematic factors (BBD). Given tables of these coefficients the angular
integrals may be evaluated rapidly and efficiently. This program was written
principally by V M Burke.
In ANG, electron configurations
are divided into two sets: a unique set and an equivalent set. Members of the
latter set have the same angular momentum properties as a member of the unique
set and differ only in the radial wavefunctions they
involve. Only the unique set need be treated in detail. Most internal files are
read and written using the filehand subpackage. Fixed record length unformatted Fortran files are treated using double buffering via the filehand interface. Program dimensions were, in 1994,
determined via preprocessing.
RMATRXII was subsequently updated
by: (1) conversion to standard Fortran 90, then Fortran
95; the introduction of dynamic memory allocation and a reorganization into a
modular structure. (2) Sparse matrix techniques and derived data types were
introduced into key parts of ANG. (3) A range of minor algorithmic and
programmatic improvements were implemented. (4) The ANG program was
parallelized on IBM architecture using OpenMP but
scaling beyond 4-5 threads deteriorated rapidly.
The ANG calculation involves the
consideration of all possible couplings from a given set of electron
configurations and the detailed angular momentum algebra needed to define an
orthonormal LSπ-coupled basis set (or, following recoupling, a
JKπ-coupled basis: for the meaning of K, see [3]). As mentioned above, the
mathematical basis of RMATRXII/PRMAT inner region formalism, in particular ANG formalism, is detailed in BBD. Essentially, ANG proceeds in
2 stages. Firstly, the surfacing coefficients required are identified and then
calculated until the appropriate surfacing coefficient table has been
completed. Then the tables are used to form all the angular couplings required
(continuum-continuum, continuum-bound, bound-bound for direct and exchange 1-
and 2-electron Hamiltonian and multipole matrix
elements). In the new code both stages are parallelized: the surfacing
coefficient calculations are distributed, the coefficients are written to a
shared memory segment which is then updated across SMP-nodes, then the second
stage is parallelized over outer loops over coupling indices in each case (c-c,
b-c, b-b etc) and output data is written in parallel.
4.2:
ParAng
The ParAng
code (ie the new ANG code) is parallelized using MPI
and assumes an SMP architecture in which there one or more nodes and an
arbitrary number of cores attached to each node. It is also assumed that there
is sufficient memory associated with each node that a single copy of the essential
surfacing tables may be kept in shared memory.
The program is written in pure Fortran 2003 and C for very low-level interactions with the
system. The C is model independent (ILP32, LP64). MPI version 2.2 is assumed.
POSIX C functions are also assumed. It is disappointing that as we approach 10
years from the publication of the Fortran 2003 standard vendors still have not
produced compliant compiler and that the
missing features severely limit the utility of those that have been
implemented. On Hector only the Nag 5.3 compiler is close to compliance. The
IBM xlf13 compiler is fully compliant.
4.2.1: ParAng Features:
·
SMP analysis using POSIX system
functions
·
MPI communicator construction for intranode and internode communications
·
IPC Shared Memory Segment storage of
R-matrix surfacing tables
·
Mutex
locking of shared-memory operations using IPC semaphores
·
Object-oriented scalable global counters
controlling MPI parallel loops
·
Generic linked-lists using polymorphic
data for temporary storage
·
MPI-IO output of results directly from
task nodes to a single unformatted disk file using double buffering and
asynchronous I/O
Here we will describe some of the
salient aspects of each of these features but will not attempt a full user
manual. i.e. the parallelization will be described but
little if any attention well be given to the physics embodied in the code or
the description of the physics input data. The overwhelming portion of the CPU
time required to perform a calculation is required in the angbb
section that performs angular integrals for bound-bound N- and N+1-electron
systems. In ParAng all sections have been
parallelized so that the entire calculation can be performed conveniently on a
single computer system. Although the code is useful primarily for larger, more
demanding calculations the code has been adapted to handle even small
calculations where there are more tasks available than the number of iterations
in the parallel loops.
4.2.2: IPC and the shm utility package
Fortran 2003 provides a standard
for interoperability with C language code. This in turn gives access to system
functions that cannot be called directly using Fortran.
The Unix System V IPC system calls provide messages, semaphores and
shared-memory. Although not portable these are universally available on unix-based systems. IPC shared-memory segments (sms) are used in the impich2 implementation of MPI. The use
of this approach in a Fortran context has been
pioneered by I J Bush and colleagues, including C Armstrong, of NAG Ltd. This
approach is informative and allows the sms approach
to fit in efficiently with MPI-1 formalism, and has been used successfully in
the materials science code CASTEP [12], but it is in certain respects
inconvenient for the present application. The routines in the ParAng code represent an entirely independent
implementation.
The IPC library functions are all
called from functions defined in the file ipc.c. The
function get_key calls the function ftok to generate an IPC key. The resulting key is required
to be unique within each system image and is generated, in this implementation,
from an integer between 1 and 99 and a file path that must be input by the
user. This path is arbitrary but must be such that a file pointed to by the
path is statable by the user. The integers are
managed within a list internal to the ParAng IPC
routines. This keeps track of IPC keys in use. Keys are obtained by one task
attached to each node and MPI broadcast to the remaining tasks. It is important
to appreciate that IPC resources (shared-memory segments, semaphores) are
limited system wide and can persist at the end of a user job. ParAng will call routines to delete these IPC objects at
the end of a job. To allow for possible job crashes or the job running out of
time the job script needs to call the functions ipcs
and ipcrm to eliminate any IPC objects owned by the
user. A shell script, segrm.sh, written by I J Bush is provided for this
purpose (the HECToR system call /usr/bin/ipcclean may also be used).
The Fortran
interface for shared-memory segments is contained in file shm.f90 and semaphore
interface in sem.f90. These modules define shm and sem derived datatypes
that contain the data pertinent to each object. For example the shm type is (so far) defined to be either integer or real
data. The datatype holds the size of the data, a
pointer to it and the segment IPC id. A set of type bound procedures define the
operations that may be performed on the segment. Finally the derived-type is
overloaded by the type constructor. The segments and mutex
locks therefore are objects in the usual object-oriented programming sense.
They may be created and destroyed as required. This is of great convenience in
this program. The Fortran 2003 finalization options
have not been used as this feature is missing from nearly all compilers.
We illustrate the shm
object:
type
shm ! shared
memory segment type
private
integer(c_int) :: keygen_id = -1 ! project id of
segment
integer(c_int) :: id =
-999 ! segment
IPC id
type(c_ptr) :: shm_address
! c-pointer to segment
integer(c_int) :: num_els ! # datatype elements
integer(c_int) :: datatype ! type of data
integer, pointer :: iptr(:) ! integer fortran
ptr to SMS
real(wp), pointer :: rptr(:) ! real fortran ptr to SMS
contains
procedure ::
attach => attach_sms
procedure :: kid
=> getId
procedure :: shmid => getShmid
procedure :: detach
=> detach_sms
procedure :: getiValue
procedure :: getrValue
generic :: get => getiValue,
getrValue
end type shm
interface shm
procedure
constructor
end interface
contains
function constructor
(count, datatype, inproc, keypath, error)
.......
The
structure of the sem.f90 module mirrors that for shared-memory segments. Apart
from creating and destroying mutex locks the allowed
operations are start_crit and end_crit
marking the start and finish of a critical section. The package comes with a
test run routine and wrapper routines for users who do not wish to use the
Fortran 2003 object structure are available, for example combining the
constructor set-up with the attach routine, and for later access. In fact, in ANG,
the routines angbb, angbc, angcc etc access the completed
surfacing coefficient tables via an intermediate module, so as not to distort
the appearance of the earlier code. The shared memory segment is accessed
within the intermediate module using shm%get(<real or integer pointer array>).
It was found by trial and error
that MPI routines could not be used reliably to determine the connectivity of
an arbitrary SMP cluster. Fortunately the POSIX library function gethostname can be used to quickly and efficiently
determine the number and names of the nodes participating in a given job. It is
then straight-forward to associate MPI ranks (within the MPI_COMM_WORLD
communicator, or a user-supplied communicator name for public variable
LOCAL_MPI_COMM in the module file comm_mpi.f90 containing the majority of MPI
calls) with each node. The gethostname function is
called in the file host.c. The remaining analysis is
performed by the module smp_analysis in file
smp_analysis.f90. The ‘proclist’ defining the tasks
associated with each node is broadcast.
In ParAng we wish to use a segment across the
whole SMP node to store the surfacing data, however the standalone package will
allow developers with knowledge of task to core assignment to subdivide this,
for example on HECToR
into groups of 8 cores.
The final file in this group is
comm_constructor.f90. As its name implies these routines set up MPI groups and
communicators reflecting the SMP structure. There are communicators allowing
data to be broadcast among the tasks corresponding to each node. A distinct
communicator is required for communication between one designated task on each node. In general the tables contained on
shared-memory segments will be partially filled by each node according to the
cases assigned to the tasks of that node. To obtain complete usable tables it
is necessary to combine the node-tables using an MPI_allreduce
sum. This uses the internode communicator. Routines in this module may be used
to check these communication patterns.
To reiterate, shm
is available as a standalone package with a test program. A more detailed
description will be given in a paper in preparation that compares the two sms packages developed on the HECToR
service, and when the code is published.
4.2.3: ParAng parallelization: SGC and generic Linked-Lists
The core of the parallelization
is to designate some key program loops as parallel. An iteration of these loops
is assigned to a single task. That task may be any task across the entire
communicator. It is important to avoid a two-way communication in order to
provide the next available iteration number to the idle task. We therefore use
the MPI one-sided RMA (remote memory access) facility to pickup and update the
counter value. This use of a global counter is ideal, as in the present case,
where there is significant variability in the CPU time required to perform a
single iteration. The examples in the MPICH package include a scalable global
counter. Scaling is achieved by setting up a tree structure and obtaining the
count by summing the nodes from the origin of the tree to a particular leaf.
This tree structure is maintained on an RMA window and so is available to all
cores. The example code was written in C. In ParAng
it has been rewritten in Fortran 2003 and incorporated
in a derived-type sgc. This counter type is provided
with type-bound procedures and put in the form of an object that can be
replicated as required. This facility is contained in the file sgc_mod.f90. The
MPI standard allows the RMA window to be exposed on a single processor. This
option has been adopted here.
One of the characteristic
problems of this angular integral calculation is lack of a convenient means of
estimating (a) the sizes of the various surfacing tables and (b) the amount of
data that must be stored for processing by subsequent stages of the
calculation. Thus initially the size of the shared-memory segments needed to
hold the surfacing tables is unknown. To circumvent this problem we require
each of the tasks to hold the surfacing data that it calculates in its own
linked-list. At the end of the surfacing calculation the relevant sizes are
known so the shared-memory segments can be constructed. Location tables are
first calculated then tasks may pop data from their linked-list and once having
obtained the mutex lock place their data in the node
surfacing tables. The data to be stored in the linked-list consists of a header
record for a particular configuration and electron shell followed by a number
of data records comprising index and coefficient data. Each set is terminated
by an end of data record. This is not easily accommodated in a traditional
linked list. The object-oriented features of Fortran
2003 make this easy. An outline of such a list has been described by PGI
consultant Mark Leair [14]. A derived link type is
defined in file gLink_mod.f90. The internal details of this module are hidden.
An unlimited polymorphic variable is used to hold the link data. The user
interface to the link module is defined by an abstract list type defined in
absList_mod.f90. Finally the user list data types are defined in the file
surf_list_mod.f90. This defines a surfList type and
derived data types sch, sc
and eod. Each of these datatypes
can be added to or popped from the list. The full list may be printed out. The
entire list may be deleted. Once the data is placed into the shared-memory
segments the memory may be retrieved by deleting the linked-list.
4.3: Parallel Filehand (pfh)
4.3.1: Introduction
The objective of this code is to obtain
an efficient parallel implemention based on MPI-IO
for use with distributed memory computers whilst preserving as far as possible
the interface and functionality of the serial filehand
code devised by V M Burke [9]. The essential features of serial filehand are a standard interface to unformatted integer or
real files using fixed length records and double buffering to improve
performance.
In parallel filehand
(pfh) the interface code is provided in the module pfilehand (pfilehand.f90). Using MPI-IO it is possible to
provide non-blocking asynchronous I/O that was not available in standard Fortran prior to the 2003 standard. If is also possible to
allow any of the tasks in the array to write directly to a single output file
thereby avoiding potential network bottlenecks if designated I/O-nodes are
used. As a trade-off we can avoid the need for synchronization and file-locking
by allowing only a single task to write to each file record. An MPI global
counter is used to assign records to each task. This implies that a file
written in parallel will comprise sets of records, each set associated with a
specific task. In order to read the information from this file in the usual
serial order it is necessary to save the starting location for
each parallel iteration. This additional location information is written
to the index portion at the start of each filehand
file. The index records have therefore been expanded to include the first 6
records by default rather than the first 2 records used by the serial filehand code. This index region may arbitrarily be
extended by adding the optional variable ‘rec_offset’
to the end of the ‘open_fhfile’ argument list. This
change requires some generalization of the serial filehand
file in order to keep track of the index writing and reading. The MPI-IO code underpining pfh is contained in
module file_io (file_io.f90). The data defining each pfh file is contained in a
abstract data type fhf. Variables of this type are
allocated and saved in an array ffiles to maintain
the usual Fortran file philosophy.
4.3.2:
pfilehand.f90
The concepts underlying the filehand and parallel filehand (pfh) packages should be kept in mind. The files are divided
into fixed-length records. Positions within the files are defined in terms of
the record-number and the position within the record. Records are defined to be
either of integer-type or of working precision floating-point type. The type
and length of each datum must be known in order to read back the file contents.
The initial records of each file are of integer-type and are used to hold
catalogues of the starting position for data items located on the remainder of
the file.
In the serial case file I/O is
provided by fortran standard
random-access files. Double buffering is employed: a buffer is written when
full or read in advance asynchronously (if the system allows this) to ongoing
computation and use of data from the other buffer. In generalizing to a
parallel package we use the MPI-IO package. Each task or core maintains it own
file-pointer. It can therefore write directly and independently to a single
disk file. Stream-io is used so that the entire file
may be viewed as a single byte stream. Each file sector is associated with a
particular core: there is therefore a ‘core-path’ (CP) of sectors associated
with each task. Provided the starting position is known, a sequence of read
operations along the CP will return the data written by that particular task.
If the CPs were written in the course of a parallel loop, the data can be
returned in serial order provided each starting position is recorded and also
processed in serial order.
We now list a selection of pfh routines that may be encountered by the user (again, a
full description will be included in the main package publication). The standalone
package includes options for wrapper routines that will group related pfh routine calls together.
·
initda initializes filehand: it is now a link to a routine in file_io.f90 that
checks the compatibility of the system’s MPI-IO and sets the buffer size
(either default or supplied as an optional argument).
·
open_fhfile
corresponds to the filehand open routine. Arguments
specify the file unit number (here used only as an id), the filename
(arbitrarily limited to 50 characters) and the ‘rtype’.
The latter logical variable is true if the file is to hold real data, false if
it is to hold integer data. The 7-character argument stats designates whether
the file is new, old or scratch. This routine simply calls the MPI-IO routine
to open the file and set up the file buffers and other information. We prefer
not to overload the standard Fortran function open –
hence the name change to open_fhfile (open filehand file). Note also that the open is for read-write
access - there is no need to close the file before reading records.
·
newfil
starts a new subfile at the next available record.
The record number is returned. In pfh the record
number is obtained from routine get_next_record_number.
·
catlog
finds the next available position on the file specified by the unit number. The
position is returned as the catalog entry interpreted
by routine lookup. The catalog array is built up for writing to the index records,
for subsequent reading.
·
{i}read{a,b,c), {i{write{a,b,c} ‘read’
or ‘write’ individual data, or 1- or 2-dimensional arrays (ie
copy to or from the buffer, initiate actual I/O in advance if required). There
will be an option for these routines to be accessed via overloaded interfaces.
·
endw
terminates writing to a subfile started by newfil. Providing the current record contains data the
remainder of the record is zeroed before writing the record to disk. This is
executed by a single task.
·
writix
signals the start of writing to the file index. Set the index flag and set the
file pointers to point to the index record and pointer.
·
endwx
signals the end to writing to the index. Resets the current record pointer and
record number before switching the index flag off. This routine did not exist
in serial filehand. Does not trigger any disk io.
·
readix is called to set
up intial reading of index and catalogue data.
·
lookup
returns the record number and file position corresponding to the provided
catalogue entry.
·
pend adds
a parallel path end symbol into the buffer
·
wr_ploop is a
special pfh routine to write parallel location data
to the index of a file. The routine also deallocates
the arrays used to hold the data. We use a MPI reduce routine to collect the
data from each task node if there are more than one node.
·
close_fhfile
Corresponds to filehand close routine. Calls the file_io routine close_mpi_file to
close the file, clean up the buffers and the global counter associated with the
file. Retrieves and prints the file statistics.
4.3.3 file_io.f90
This module contains routines making
the MPI-IO calls central to the operation of pfh.
These are ordinarily not user visible or called directly but are accessed via
the wrapper functions in pfilehand. Conceptually each
task writes a chain of records: the end of each record contains the record
number of the next record in the chain. The data written by each task can
therefore be retrieved by reading sequentially along each of the task chains, The records to be used are assigned by calling a file
specific global counter, There is an offset of file_offset
so that file_offset records at the start of each file
are reserved for use as the file index. When executing a parallel loop we
expect, in general, that each task will process a number of loop iterations. In
order that the records can be read back in a sequential order it is necessary
to know the disk location (record number and record pointer) where the data
from each loop iteration begins. Routines are provided for saving these loop
iteration locations. These are start_ploop, save_ploc and end_ploop. Up to 5
(by default) loops may be saved in this way. If the order in which the output
of each loop is unimportant, then there is no need to retain this data. In the
final package these and routine write_partial_buffers
will be aliased or set up as links in the main pfilehand
module as they are required outside the package.
·
open_mpi_file This
routine initializes the data of the fhf member that
corresponds to a particular element of the ffiles
array. This (unwieldy) scheme is meant to minimize storage requirements as only
the elements corresponding to active files are allocated. The option of
defining a ‘file’ object does not permit a Fortran-like naming scheme in which
the file is identified by a unique file number. This routine also allocates the
buffers to be used by the file. There are normally two buffers. In the case of
real files these are supplemented by additional integer buffers to accommodate
the writing of index records. This routine also calls the constructor for the
global counter used to allocate records of the file.
·
write_mpi_record This
routine waits until the I/O-buffer is available. The buffers are then swapped
so the old I/O-buffer becomes the current active buffer. A new record number is
obtained and appended to the end of the IO-buffer. A non-blocking
(asynchronous) write of the filled buffer to disk is then initiated. This
routine is triggered when a task has filled its current active buffer of if the
file is to be closed. In the latter case all records containing data must be
written to disk. In this case the unused portion of the buffer is zeroed before
writing. It is assumed that index records are only written by node 0.
·
read_mpi_record This
will read one record of the file or from the file index if the index flag is
set. It is assumed that consecutive records of a record chain will be read by
default. In this case the read operation is performed using MPI-IO non-blocking
reads and checks are performed to ensure that a record is available. The
initial read at the start of a chain is necessarily blocking and is treated
separately.
·
set_mpi_record is
used to reposition a file at the start of a (parallel) sub-file and perform a
blocking read, after checking whether this is necessary, ie
if the required next record is different from that written into the index. This
allows reading to be independent of the communicator and sgc
used to write the file. The blocking read is required if the pre-buffered data
and previously initiated non-blocking read are out of sequence for the reading
communicator and sgc.
·
close_mpi_file must first write
to disk any partially filled records. Once this is completed the file may be
closed and the file buffers deleted. As part of the closure process the file
counter is destroyed and the file statistics written.
·
get_mpi_stats
collects the total number of records written by all the tasks and also the
maximum record number used by write_mpi_record. The
latter determines the total size of the file. The routine is called by close_mpi_file.
·
get_next_record_number
calls the global counter to find the next available record number. This is
declared public but would not normally be called externally.
·
del_record_ctr
destroys the global counter releasing RMA windows. Should not be called
externally.
Parallel Loops
As the data on the file that is
written during a parallel loop is not in the usual serial order we create a
special location index that records the starting position of the data for each
configuration in a particular parallel loop, The indices for each computing
task are combined on task 0 to form a complete index, ploc(0:<#iterations>).
Redundant tasks not needed to perform an iteration
must skip the parallel loop. A count of these skips is recorded in ploc(<#iterations>).
·
start_ploop is
called prior to the execution of a parallel loop. It allocates arrays ploc on each core to hold iteration location data.
·
save_ploc is
called by each task when it starts a parallel loop iteration. It adds the
current file location data to its copy of the location array ploc. Subsequent disk I/O by the task will be in the chain
of records beginning at the stored location.
·
end_ploop is
called globally by all tasks on exiting from a parallel loop. The routine uses
an MPI collective reduce call to combine the location lists of each task on
task 0. The partial ploc indices on the cores are
then deleted.
·
write_partial_buffers At
the end of a run in which multiple tasks are used write a pfh
file there will partially filled buffers in memory on each core. This routine zeroes
the unused portion of these buffers and writes them to disk. This routine must
be called prior to closing a file that has been opened for writing. There is no
need to call this routine before closing a file open for reading.
There are several issues.
Firstly, the numbers that are appended to the end of each record are of type integer(MPI_OFFSET_KIND) and are likely to be 8-byte
integers for most processors. These numbers are therefore handled using the
transfer intrinsic function. Routines are called at the beginning of the run to
check and print the sizes of the various numbers being used. This insures that
the record sizes are consistent and can be read (perhaps with some adjustments)
on other computers. Note that we have chosen to use different record lengths
for integer files and real files. The objective has been to carry the data
defining a particular filehand file around in a
derived datatype. In order to follow Fortran practice and serial filehand
we use a ‘unit number’ to identify operations on each file. This kind of
labelling does not allow a simple definition of a file ‘object’.
A test run of pfh
is provided by the file test_filehand.f90. This includes a parallel write of a
set of data followed by an independent parallel read-back of the same data.
The particular advantage of
serial and parallel filehand in the R-matrix codes is
that the data produced by ANG is likely to be re-used many times in HAM in an
unpredictable order. Hence the use of direct access files originally and now
MPI-IO files to allow for the independent parallel writing and reading. The
much larger capacity of modern machines to store data in memory may be taken
account of by the choice of the buffer size, however
the current and envisaged calculations are such that the package will remain a
vital component of the R-matrix package. Each type of matrix element component
calculated in ANG has two files associated with it: an integer file containing
labels and indices and a real file containing the associated coefficients.
4.4 Tests of ParAng
We present results for 2 test
cases, the oxygen case used for RAD tests, and a much larger case for Fe+
that cannot be run on HECToR with serial ANG. The
iron test is of the order of calculations currently being run by users and at the
lower end of planned calculations. The NAG compiler was used at –O3 level. In
both cases the bulk of the execution time was taken up by routine ‘angbb’ which calculates ‘bound-bound’ angular couplings.
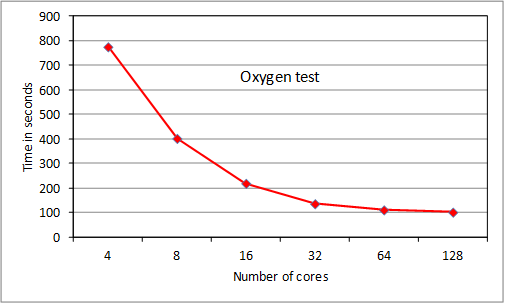
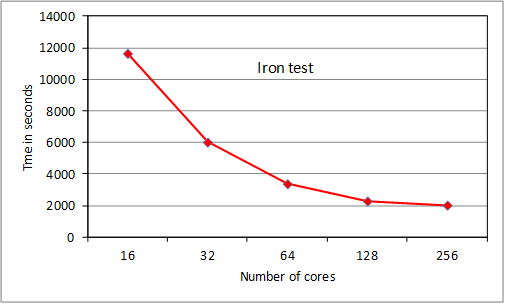
Figure 5. Tests of ParAng
The
oxygen test scales extremely well to 32 cores, then scaling starts to drop off
as MPI overhead becomes noticeable. We note that the original serial ANG code
took, respectively: 1973s, 2152s and 1475s with gnu, pgi
and cray compilers (-O3 level, -fast for pgi) as single jobs on a 32-core node. Thus we wait for the
Fortran 2003-compliant cray
compiler to be fully debugged as performance should improve considerably. The
iron case scales extremely well to 64 cores and reasonably well with some MPI
overhead noticeable at 128 cores. Scaling is tailing off at 256 cores. These
results were obtained following some testing of varying the pfh
buffer size, which had a noticeable effect for runs using more than 1 node: the
default size was reset (increased from the serial filehand
value) to produce the results. Repeats of tests showed some variation of up to
about 5% in execution time for the 4 and 8 node Fe+ runs, attributed
to variations in the sgc procedure: this will be
investigated (section 6). For an upgraded release, ParAng
is currently being subjected to detailed parallel profiling to identify the
main overhead bottlenecks and reduce them. However the current scaling at 256
cores is as good as for many other established quantum physics and chemistry
codes on HECToR, and will improve for larger cases.
Thus, apart from the new packages, we have transformed a serial code into a
parallel code which should scale well to more than 256 cores for the complex
atomic cases planned by the user community.
5.
Detail: HAM
The HAM module performs the task
of constructing the Hamiltonian matrix elements corresponding to a set of
scattering symmetries. These matrix elements are written to disk files as input
to PDG, or are diagonalized directly. The program
stage also performs a number of subsidiary tasks: it constructs and diagonalizes target Hamiltonians; it forms asymptotic
potential coefficients (multipole potential
coefficients of the potential defining the scattering in the region where the
incident electron and the target are distant from one another) and dipole
coefficients used to calculated photoionization cross sections and in the multiphoton codes [6,7]. None of
these tasks is particularly CPU-intensive. The core task of constructing
Hamiltonian elements is, however, data intensive and we have incorporated the pfh code to cope with this.
The ‘ij’-th Hamiltonian matrix element is a
linear combination of one-electron and two-electron radial integrals computed
in RAD multiplied by coefficients computed in the ParAng
code. For many R-matrix calculations the number of radial elements is not
excessive and these elements may be read into memory and simply selected for
use as required. For certain intermediate energy calculations this number may
become sufficiently large that a more elaborate partitioning scheme must be
employed. The new code ParHam allows radial elements
to be read in using pfh. The angular coefficients and
associated indices must be read from pfh parallel
files.
The indices of the ANG files are
read. The last block of data from each of these file sections is the location
data providing the location on disk that corresponds to the start of a parallel
path (a linked list of file records written by a single task). There is one set
of locations for each parallel loop - and one location for
each loop iteration. There are always two associated locations - the
location in the integer file of the index information and the location in the
real file of the coefficient information. This information is combined into a
data object ‘ploc’ in the module plc_mod
contained in file plc_mod.f90. Using type-bound procedures we associate the datatype and its methods to form an object (in the
object-oriented sense) that is convenient to use throughout ParHam.
Once the files are correctly positioned the ‘plc’ constructor is called to
define the ploc object. The main method is the ‘ptr’ method that returns pointers to the data for a given
parallel loop.
In the case of bound-bound matrix
elements, treated in bb_ham.f90, it is necessary that two sets of parallel
location data are returned. The loop that corresponds to the one used to write
the parang file is now read back in parallel using
all available tasks. Tasks are assigned using the scalable global counter sgc exactly as was done in ParAng.
The loop is initiated by selecting the ploc data
according to the assigned loop iteration. The locations are converted to
records and record offsets by calling the lookup utility from pfh. The files are then independently positioned by each
task using set_mpi_record. The Hamiltonian element is
then constructed. It is finally planted directly in the output file is the
required position. bb_ham is
used first to construct target Hamiltonians and later the bound-bound submatrix of the N+1-electron Hamiltonian.
The bound-continuum submatrix is constructed in a completely similar manner by
the routine hambc contained in the file rdhmat.f90.
Again the same loop over consfgurations used in ParAng is selected for parallelization. In this case only a
single set of pointers are required for each parallel loop. In each of these
modules there are routines for locating the radial integrals required for a
given case. e.g. locbc for
the bound-continuum two-electron radial integrals, loc1bc for the
bound-continuum one-electron radial integrals.
The continuum-continuum parts are
somewhat more involved as it is necessary to sum over the target eigenstates that are optionally computed at the first stage
of the ParHam calculation. The full N+1 electron
Hamiltonians are computed in stgmatf (non-exchange
contribution) and stxmatf (exchange contribution).
The corresponding ParAng files are read in routines
in the module ang_ctl, file ang_ctl.f90. The files
for the exchange data are read by rd_ang_data and
those for direct data by rd_angd_data. Again ploc objects are used in the file positioning. In this case
the angular data is read prior to performing the parallel loops. We have paid
particular trouble to detect and print errors detected by the system and now
exported by Fortran as syserr
or ioerr, similarly the strings provided by MPI-II.
Error halts are all via an error module which ensures that MPI is shut down
cleanly.
Some of the output files, the
H-file and the TARMOM-file, are intended for immediate use by follow-on
R-Matrix programs (either FARM, PFARM, the relativistic recoupling codes or alternative
programs). These files could be run on different computers than used for RAD, ParAng and ParHam. For this
reason we have allowed for the possibility of a portable data representation
for these files. Note that the external32 presentation defined in the MPI-2
standard is not available in mpich2. For this reason we have adopted the XDR
representation defined by SUN for IPC as an option for output. This is a 32-bit
representation which suffices for the present programs. Coding/Decoding
routines are available as part of the standard library of effectively all
computers. These are C-callable and therefore we have designed a standard Fortran interface, nxfiles.f90 (part of ‘xstream’,
see [4]) that allows files to be written in either XDR or native representation.
The XDR data is buffered for encoding and decoding in order to allow arbitrary
buffer sizes to be used for both processes. This part of the calculation is
performed by the routines in buf_mio.c. To simplify
the options these files are written by MPI-IO explicit-offset C-callable
routines. Files of matrix elements intended for the use in subsequent parallel
calculations are output using pfilehand and the
native representation.
As noted in section 2, ParHam is, at the time of writing, undergoing extensive
validation and profiling tests. Scaling and performance data will be added in
an update to this report.
6. Brief perspectives
Apart
from the profiling and optimization already mentioned, ongoing verification
tests and work to be performed as a result of user testing and feedback from
real applications, there are some computational aspects that can be explored
further. The RAD code provides a more straightforward opportunity for detailed
investigation of the load-balancing of the sgc
module. Conversely, given the efficiency
of the new RAD code, it may be possible to introduce some localized fine grain OpenMP into inner loops of ParAng,
to reduce the overall number of MPI tasks while still making full use of the
nodes. Similar possibilities will become apparent for ParHam.
There are also possibilities for further development of pfh,
including the introduction of shm as a user-invisible
lower layer, most obviously to keep the indexing data as a shared memory
segment (each task writes to a different location) and more ambitiously to make
the main buffer arrays shm objects, to reduce
communication overheads. This project has directly contributed to the upgrading
of compilers towards correct Fortran 2003 compliance,
and we aim to continue this encouragement and pressure, with the help of HECToR staff and successors on next-stage platforms.
About the
Authors
Professor
Cliff Noble (cliff.noble@stfc.ac.uk) is a
visiting professor at the Department of Computational Science and Engineering
at STFC Daresbury Laboratory. His previous role was
Head of the Atomic and Molecular Physics Group in the department. The focus of
his work is developing codes that calculate atomic and molecular collision
processes using high performance computers.
Dr
Andrew Sunderland (andrew.sunderland@stfc.ac.uk) is a computational scientist in
the Advance Research Computing Group, Computational Science and Engineering, at
STFC Daresbury Laboratory. His work involves the
development, optimization and analysis of scientific codes and parallel
numerical algorithms.
Dr Martin
Plummer (martin.plummer@stfc.ac.uk) is
a computational scientist and Group Leader for Theoretical Atomic and Molecular
Physics in the Advanced Research Computing Group, Computational Science and
Engineering, at STFC Daresbury Laboratory. He also optimized and managed various codes
on the UK HPC service HPCx with particular responsibility for the materials
science code CASTEP.
All the above
authors can be contacted at:
STFC Daresbury Laboratory,
Warrington,
WA4 4AD
United
Kingdom
Tel: +44 1925
603000
This project was funded
under the HECToR Distributed Computational Science
and Engineering (CSE) Service operated by NAG Ltd. HECToR
– A Research
Councils UK High End Computing Service - is the UK's national supercomputing
service, managed by EPSRC on behalf of the participating Research Councils. Its
mission is to support capability science and engineering in UK academia. The HECToR supercomputers are managed by UoE
HPCx Ltd and the CSE Support Service is provided by
NAG Ltd. http://www.hector.ac.uk . We also acknowledge the
original work on these codes by the BBD authors, particularly V M Burke, and by
H W van der Hart on the OpenMP RAD code and sections
of the HAM code.
References
1. The UK-RAMP consortium
is a 5-year EPSRC Software Development Call Grant shared between Queen’s
University Belfast, UCL, the Open University and STFC Daresbury
Laboratory, commencing 1 October 2009 (EP/G055416/1, EP/G055475/1,
EP/G055556/1,
EP/G055599/1); CCPQ details at http://www.ccpq.ac.uk
2. A G Sunderland, C J Noble, V M Burke and P G Burke, Comput. Phys. Commun. 145 (2002) 311-340
3.
P G Burke,
‘R-matrix Theory of Atomic Collisions: Application to Atomic, Molecular and
Optical Processes’, Springer, 2011
4. ‘Future-proof parallelism for electron scattering codes,’ A G Sunderland, C J Noble and M Plummer, http://www.hector.ac.uk/cse/distributedcse/reports/prmat/
5.
V M Burke and C J Noble, Comput.
Phys. Commun.
85 (1995) 471-500; V M Burke, C J Noble, V Faro-Maza,
A Maniopoulou and N S Scott, Comput. Phys. Commun. 180 (2009) 2450-2451
6. M A Lysaght, P G Burke and
H W van der Hart, Phys. Rev. Lett. 101 (2008) 253001;
Phys. Rev. A 79 (2009) 053411; A C Brown, S Hutchinson, M A Lysaght and H W van
der Hart, Phys. Rev. Lett. 108 (2012) 063006
7. L R Moore, M A Lysaght, L A A Nikolopoulos, J S Parker, H W van der Hart and K T Taylor,
J. Mod. Optics 58 (2011) 1132-1140; L R Moore, M A Lysaght, J S Parker, H W van
der Hart and K T Taylor, Phys. Rev. A 84 (2011) 061404
8. http://ccpforge.cse.rl.ac.uk
9. P G
Burke, V M
Burke and K
M
Dunseath, J. Phys. B: At. Mol. Opt. Phys. 27 (1994)
5341
10. http://www.prace-project.eu
11. http://software.intel.com/en-us/articles/intel-parallel-inspector/
12. I J
Bush, Technical Report HPCxTR0701 www.hpcx.ac.uk/research/hpc/technical_reports/HPCxTR0701.pdf , A Maniopoulou and
C Armstrong, NAG HECToR Case Study CSE Report (2009) http://www.hector.ac.uk/cse/reports/castep_m.pdf
13. K A Berrington, W B Eissner and P H Norrington, Comput. Phys. Commun 92 (1995) 290-420 (this article subsumes earlier
publications of the package)
14. http://www.pgroup.com/lit/articles/insider/v3n2a2.htm