Next: ScaLAPACK Performance Profiling Up: Methfessel-Paxton Approximation to Step Previous: Methfessel-Paxton Approximation to Step Contents
 |
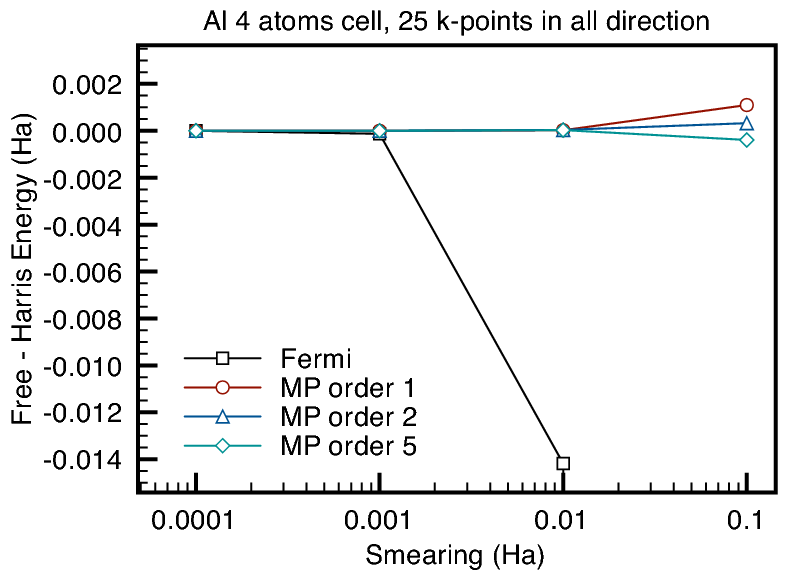 |
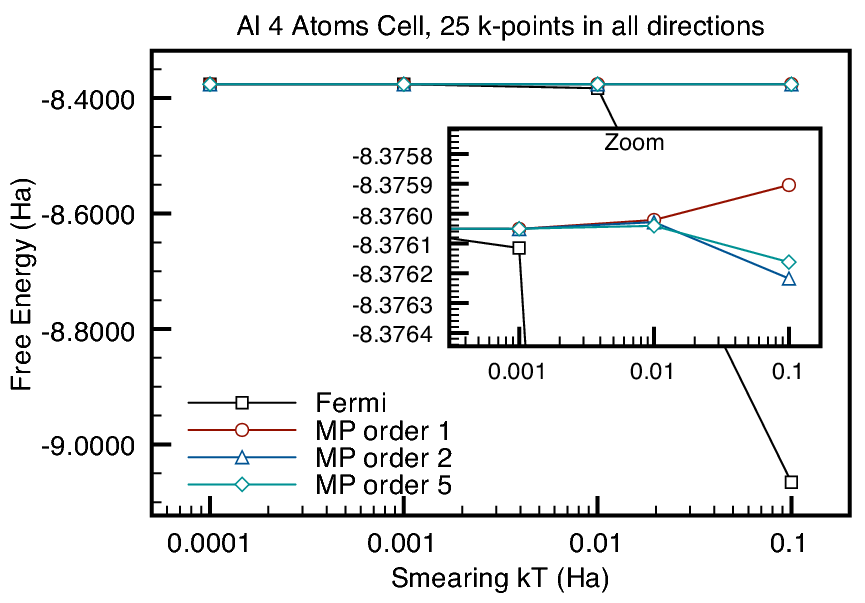
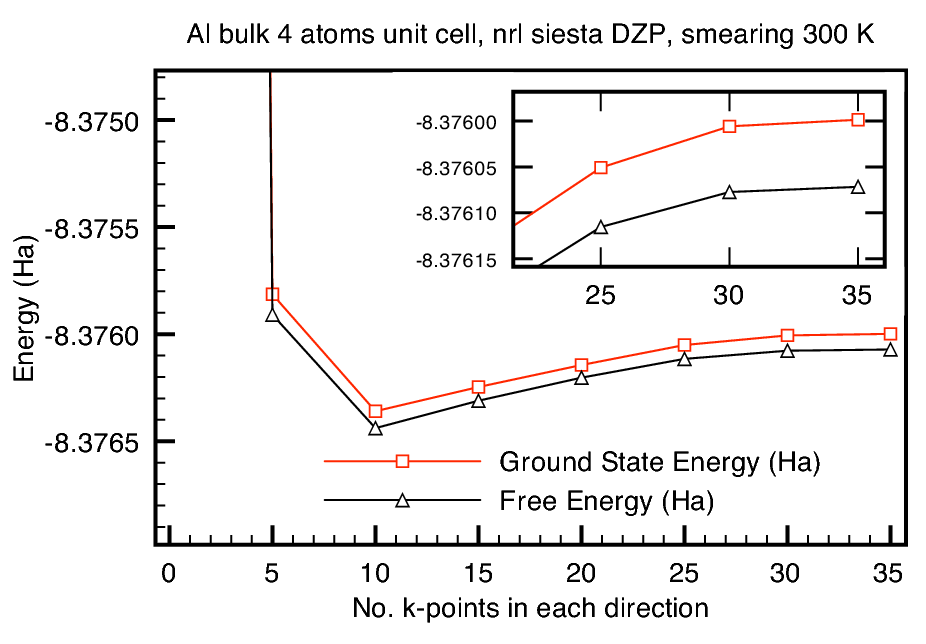
Figure 6 shows the comparison between calculations
on a 4 atom unit cell aluminium bulk using Fermi and Methfessel-Paxton
smearing methods. We only did non-self-consistency calculations. We
can see that Fermi smearing leads to different energy results as we
increase smearing factor ![]() . We can see that the difference
between Free energy and the calculated ground-state energy (we called
it Harris energy) also increased dramatically for Fermi smearing. This
is expected as the smearing does correspond to the physical temperature and
as
. We can see that the difference
between Free energy and the calculated ground-state energy (we called
it Harris energy) also increased dramatically for Fermi smearing. This
is expected as the smearing does correspond to the physical temperature and
as ![]() increases we depart from the zero-temperature regime. On the
other hand, the smearing in Methfessel-Paxton method is just a
parameter used in the approximation. And we can see that increasing
increases we depart from the zero-temperature regime. On the
other hand, the smearing in Methfessel-Paxton method is just a
parameter used in the approximation. And we can see that increasing
![]() has small effect on the energies calculated using
Methfessel-Paxton smearing and results also improve as the order of
Hermite polynomials used increases. This means a relatively large
smearing factor can be used under Methfessel-Paxton approximation,
which allows fewer
has small effect on the energies calculated using
Methfessel-Paxton smearing and results also improve as the order of
Hermite polynomials used increases. This means a relatively large
smearing factor can be used under Methfessel-Paxton approximation,
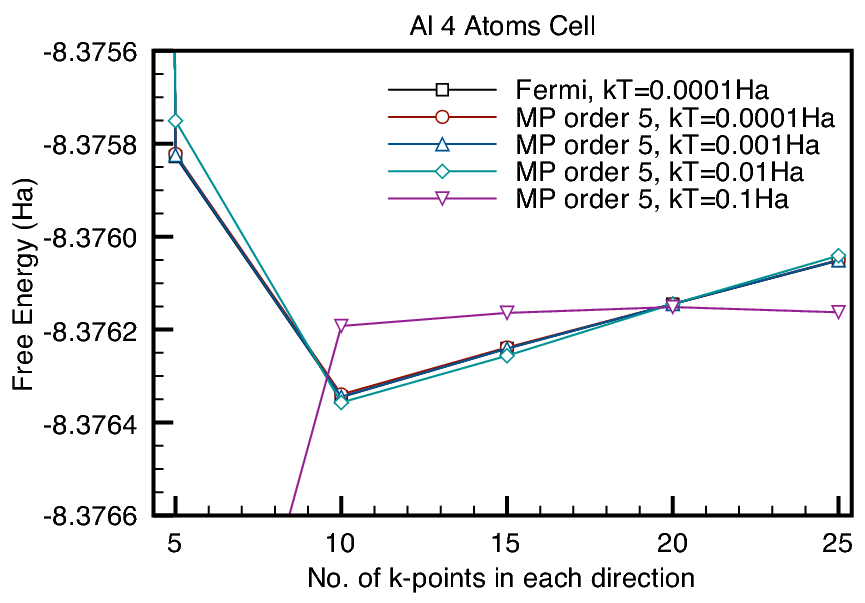
which allows fewer ![]() -points. To be more specific, figure
7 shows that for smearing factor
-points. To be more specific, figure
7 shows that for smearing factor
![]() , (corresponding to smearing temperature
of about 31565.51 K), we reach
, (corresponding to smearing temperature
of about 31565.51 K), we reach ![]() -point convergence at about 10
Bloch space (
-point convergence at about 10
Bloch space (![]() ) points per each reciprocal lattice direction,
while the total energy will be within
) points per each reciprocal lattice direction,
while the total energy will be within ![]() Ha of the ground state
energies calculated using low smearing and large number of
Ha of the ground state
energies calculated using low smearing and large number of
![]() -points. This is compared with the requirement of 25
-points. This is compared with the requirement of 25
![]() -points for convergence with a small smearing factor, see
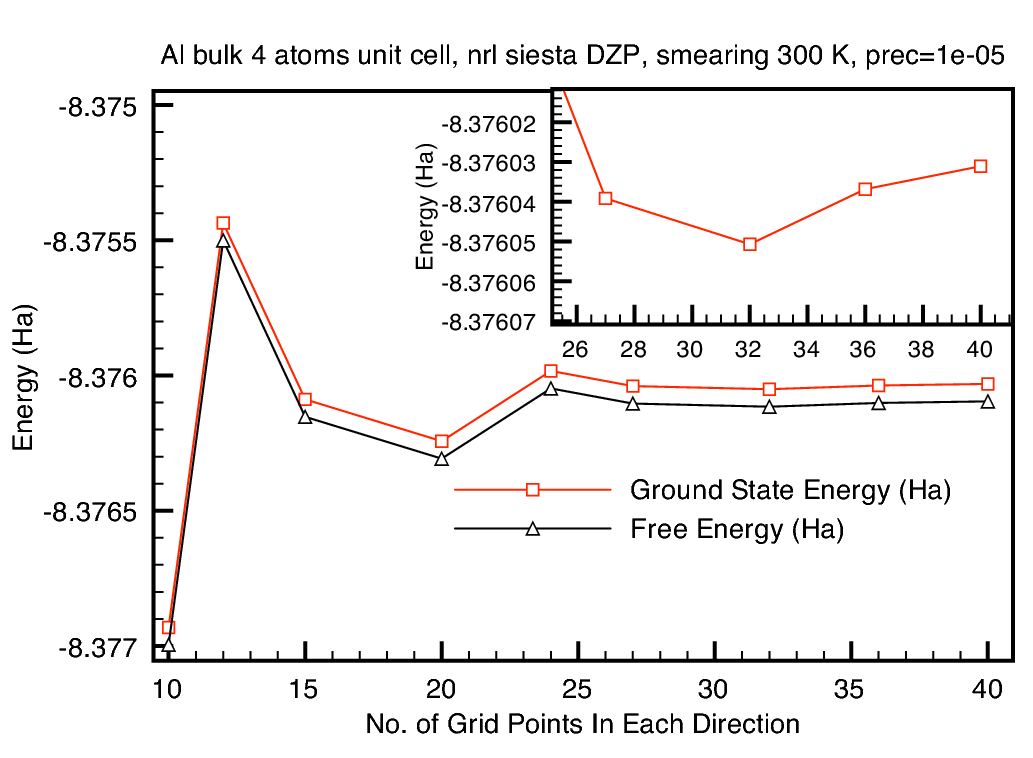
figure 8.
-points for convergence with a small smearing factor, see
figure 8.
 |
 |
 |
Lianheng Tong 2011-03-02