Implementation

We introduced a new user definable parameter $N_G$, denoting the number of processor groups each responsible for different set of $\vec{k}$ points. We want to allocate a set of $N^G_\vec{k}(n_G)$ points to each process group $n_G$ ( $n_G = 1, \dotsc, N_G$), and then the $N^G_P(n_G)$ processing-nodes inside each group will work on the $N^G_\vec{k}(n_G)$ points. The cyclic allocation technique is the most efficient in terms of evenly distributing the work-load. So that the process-group indices $n_G$ relates to processing-node indices $n_P$ and $\vec{k}$-point indices as

$$n_G = \mathrm{mod}((n_p - 1), N_G) + 1$$ (14)

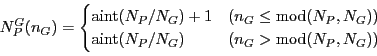and $$n_G = \mathrm{mod}((n_\vec{k} - 1), N_G) + 1$$ To work out $N^G_P$ we have $$N^G_P(n_G) = \begin{cases} \mathrm{aint}(N_P / N_G) + 1 & (n... ...rm{aint}(N_P / N_G) & (n_G > \mathrm{mod}(N_P, N_G)) \end{cases}$$ and similarly $$N^G_\vec{k}(n_G) = \begin{cases} \mathrm{aint}(N_\vec{k} / N... ...vec{k} / N_G) & (n_G > \mathrm{mod}(N_\vec{k}, N_G)) \end{cases}$$

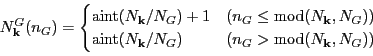
We introduced arrays $\var{pg_procs}(1:N_G, N^G_{P\text{max}})$ and $\var{pg_kpoints}(1:N_G, N^G_{\vec{k}\text{max}})$ to keep track of which processors and $\vec{k}$ points are allocated to which processor groups. These arrays can be worked out following the steps given in algorithm 2. Note however that the algorithm is order $N_P^2$ (where $N_P$ is total number of processors), because the same algorithm is repeated on every processor. However the calculations are simple and one only has to do it once at the beginning of the calculation; further more no communication is needed between the processors.

The goal is to define a mapping between the ScaLAPACK block cyclic format distributed over a processor grid consisting of only a subset of processors for a given $\vec{k}$ point and the native CONQUEST format that distributes the rows of the matrices into primary set atoms and partitions across the entire set of processors. In the original CONQUEST implementation, to aid the mapping a reference matrix format is introduced. This is the format for the matrices $\tilde{H}\ind{^{\vec{k}}_{i\alpha,j\beta}}$ and $\tilde{S}\ind{^{\vec{k}}_{i\alpha,j\beta}}$ which has the same form as if one writes them down on for calculations on paper. The reference format matrices are never physically stored. Also in the original implementation by noticing the fact that the order of atoms in a calculation can be arbitrary, the atomic ordering of the rows of the ScaLAPACK format is chosen to be the same as that of the native CONQUEST format. In other words the atomic ordering (index $i$) of the ScaLAPACK matrices $\tilde{H}\ind{^{\vec{k}}_{i\alpha,j\beta}}$ and $\tilde{S}\ind{^{\vec{k}}_{i\alpha,j\beta}}$ is chosen to be the same as the ordering of $i$ in matrices $H_{i\alpha,n\beta}$ and $S_{i\alpha,n\beta}$ stored in CONQUEST format. We have kept this requirement for the implementation $\vec{k}$ point parallelisation.

Figure 11: Schematic showing the mapping between native Conquest format matrices and the corresponding square matrices in ScaLAPACK and reference format.

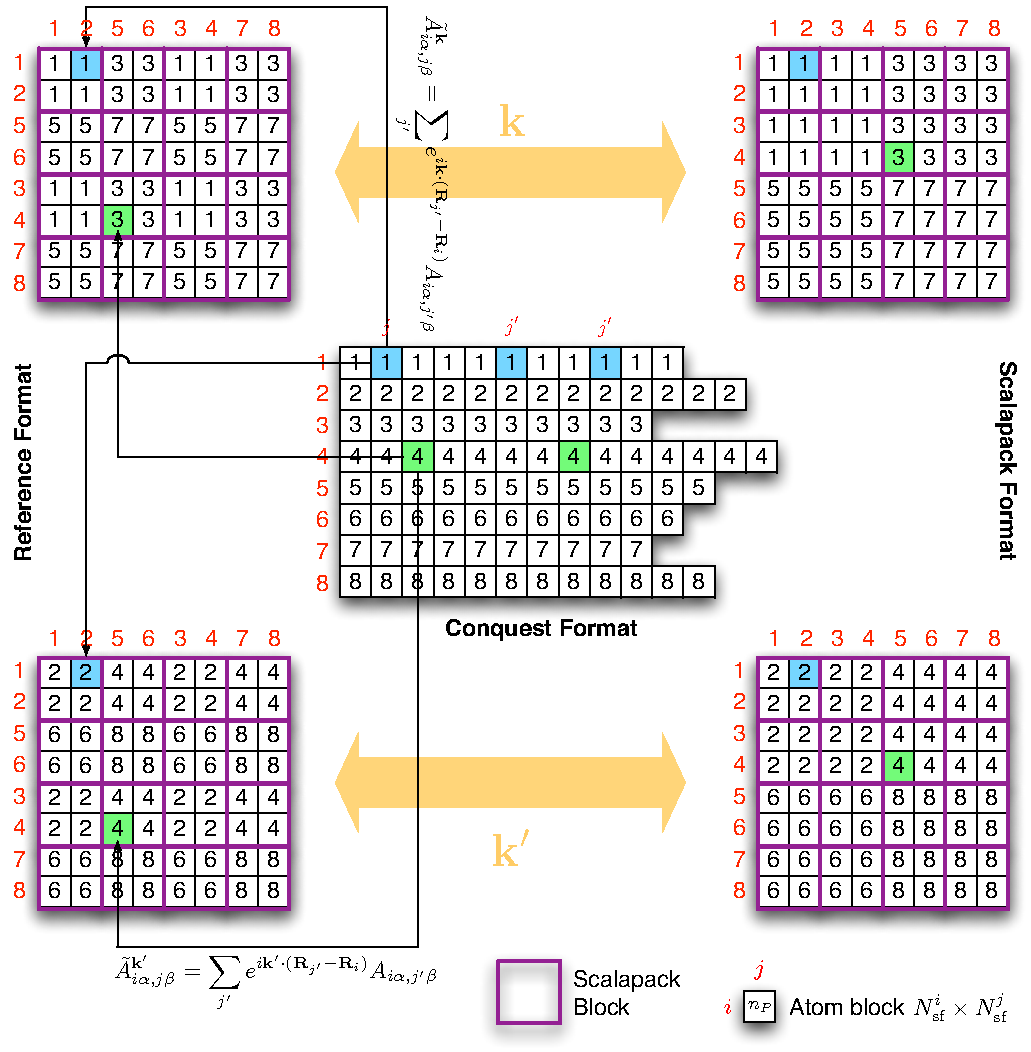Figure 11 shows the possible mapping of matrices if there are 8 processors in total and the user have chosen 2 processor groups. The BLACS process grid is assumed to be $2 \times 2$ and the ScaLAPACK blocks are shown in purple boxes. Due to cyclic allocation, the first group will have processors 1, 3, 5, 7 (note we are indexing the processors from 1) and the second group have processors 2, 4, 6, 8. The ScaLAPACK matrix for each group have identical format, and the matrix elements differ only by the way different $\vec{k}$ point is used to generate $\tilde{H}\ind{^{\vec{k}}_{i\alpha,j\beta}}$ or $\tilde{S}\ind{^{\vec{k}}_{i\alpha,j\beta}}$ matrices from the CONQUEST matrices $H_{i\alpha,n\beta}$ or $S_{i\alpha,n\beta}$. The coloured squares in the CONQUEST matrix shows the periodic images of atoms all belong to the neighbourhood of a given primary set atom. And their contributions are summed up according to equation (18) and stored in the corresponding coloured location in the ScaLAPACK matrix. The numbers inside the small boxes identify the processor responsible for the data block.

Since the atomic ordering of rows and columns of the ScaLAPACK is unchanged from the original implementation, subroutines find_SC_row_atoms, find_ref_row_atoms and find_SC_col_atoms of the ScalapackFormat module do not need to be modified. However the rest of the module as well as the data transfer modules in module DiagModule do need modification, to take into account that now the maps to BLACS processor grid is also dependent on the processor group we are in, and we have to send one copy of the matrices to each of the $N_G$ processor groups.

To obtain the eigenvectors the ScaLAPACK subroutine pzhegvx call is made on every processor, with each processor group using a different set of $\tilde{H}\ind{^{\vec{k}}_{i\alpha,j\beta}}$ and $\tilde{H}\ind{^{\vec{k}}_{i\alpha,j\beta}}$ (corresponding to a different $\vec{k}$). Upon return from the ScaLAPACK call each processor group will have a different set of eigenvectors. To build the density matrix we first map the ScaLAPACK format eigenvectors into the native CONQUEST format, then accumulate the products of the eigenvectors one $\vec{k}$ point at a time (see equation (19)). This is preferred because we can then utilise the pre-existing code for generating density matrix, and only one storage array for eigenvectors in CONQUEST format is needed on each processor--as contributions from eigenvectors are accumulated into the density matrix. Also performance wise the main benefit of $\vec{k}$ point parallelisation comes from the freedom it offers for optimising the ScaLAPACK routine, and building the density matrix is simply a scalar multiplication and accumulation process hence it is perfectly efficient to build the density matrix using the parallel processing format provided by the native CONQUEST approach (please read [5] for details on how matrix operations are handled in CONQUEST).

Figure 12: Matrix formats before and after pzhegvx call

Some attention needs to be paid on the mapping from the output eigenvectors distributed following the ScaLAPACK block-cyclic format and the BLACS processor grid, to the distribution format for matrices used by CONQUEST. First important fact to note is that the ScaLAPACK subroutine pzhegvx returns the eigenvectors in columns and in the same order as the corresponding eigenvalues (see Figure 12). On the other hand, in CONQUEST format for each $\vec{k}$ each processor is required to be in charge of a set of atoms in FSC, in other words, a set of indices $i\alpha$ for the eigenvectors $c\ind{^{\vec{k}}^{i\alpha}_n}$. And unlike the cases with conventional matrices in CONQUEST which are stored in row-major format (i.e. not strictly a matrix in FORTRAN 90 sense), the eigenvectors are stored as a two-dimensional array. We require the $c\ind{^{\vec{k}}^{i\alpha}_n}$ data associated to each $i\alpha$ index to stay in one continuous piece of memory, this means a column-major storage for the eigenvector. In other words in CONQUEST format the eigenvectors are stored as $c\ind{^{\vec{k}}_{n}^{i\alpha}}$. That is, the eigenvectors are stored in rows. The order of eigenvalues also changes from the ScaLAPACK format, because the CONQUEST format ordering should be the same as that of the reference format.

The steps taken to generate the new density is illustrated in pseudocode algorithm 3. One has to be careful that we do not step over the limits since it is highly likely that number of $\vec{k}$ points in each processor group is different, and hence an if statement is required to ensure this.