


Next: 5. Independent Band Optimisation
Up: castep_performance_xt
Previous: 3. Band-Parallelism (Work Package
Contents
Subsections
The first stage of the project included the distribution over the
band-group of the calculation of the band-overlap matrices required
for both orthonormalisation of the wavefunction and the subspace
Hamiltonian. These matrices still need to be diagonalised (or
inverted) and Castep 4.2 does this in serial. These operations scale
as 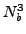 so as larger and larger systems are studied they will start
to dominate. For this reason the second stage of the project involves
distributing these operations over the nodes.
so as larger and larger systems are studied they will start
to dominate. For this reason the second stage of the project involves
distributing these operations over the nodes.
Because the aim of this stage of the project was to implement a
parallel matrix diagonaliser and inverter, which is independent of
most of Castep, we created a testbed program to streamline the
development.
The subspace diagonalisation subroutine in Castep uses the LAPACK
subroutine ZHEEV, so we concentrated on that operation
first. The testbed program creates a random Hermitian matrix, and uses
the parallel LAPACK variant ScaLAPACK to diagonalise it.
The performance of the distributed diagonaliser (PZHEEV) was compared to that
of the LAPACK routine ZHEEV for a range of matrix sizes.
Table 4.1:
Hermitian matrix diagonalisation times for the ScaLapack
subroutine PZHEEV.
| |
time for various matrix sizes |
| cores |
1200 |
1600 |
2000 |
2400 |
2800 |
3200 |
| 1 |
19.5s |
46.5s |
91.6s |
162.7s |
|
|
| 2 |
28.3s |
65.9s |
134.6s |
|
|
|
| 4 |
15.8s |
38.2s |
54.7s |
90.1s |
|
|
| 8 |
7.9s |
19.0s |
37.6s |
63.9s |
81.6s |
|
| 16 |
4.3s |
10.5s |
20.3s |
32.5s |
76.2s |
|
| 32 |
2.7s |
6.0s |
11.6s |
19.2s |
43.1s |
|
|
An improved parallel matrix diagonalisation subroutine,
PZHEEVR
(The `R' is because it uses the Multiple
Relatively Robust Representations (MRRR) method)
, was made available
to us by Christof Vömel (Zurich) and Edward Smyth (NAG). This
subroutine consistently out-performed PZHEEV, as can be seen from
figure 4.1.
Figure 4.1:
A graph showing the scaling of the parallel matrix
diagonalisers PZHEEV (solid lines with squares) and PZHEEVR (dashed
lines with diamonds) with matrix size, for various numbers of cores
(colour-coded)
|
|
The ScaLAPACK subroutines are based on a block-cyclic distribution,
which allows the data to be distributed in a general way rather than
just by row or column. The timings for different data-distributions
for the PZHEEVR subroutine are given in table
4.2.
Table 4.2:
PZHEEVR matrix diagonalisation times for a 2200x2200 Hermitian
matrix distributed in various ways over 64 cores of
HECToR.
| Cores used for distribution of |
|
| Rows |
Columns |
Time |
| 1 |
64 |
6.48s |
| 2 |
32 |
6.45s |
| 4 |
16 |
5.80s |
| 8 |
8 |
5.92s |
|
The computational time 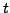 for diagonalisation of a
for diagonalisation of a 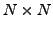 matrix
scales as
matrix
scales as 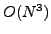 , so we fitted a cubic of the form
, so we fitted a cubic of the form
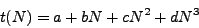 |
(4.1) |
to these data for the 8-core runs. The results are shown in table
4.3. This cubic fit reinforces the empirical
evidence that the PZHEEVR subroutines have superior performance and
scaling with matrix size, since the cubic coefficient for PZHEEVR is
around 20% smaller than that of the usual PZHEEV subroutine.
Table 4.3:
The best-fit cubic polynomials for the PZHEEV and PZHEEVR
matrix diagonalisation times for Hermitian matrices from
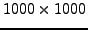 to
to
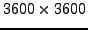 distributed over 8 cores of
HECToR.
distributed over 8 cores of
HECToR.
| Coefficient |
PZHEEV |
PZHEEVR |
| a |
-1.43547 |
-0.492901 |
| b |
0.00137909 |
0.00107718 |
| c |
9.0013e-08 |
-7.22616e-07 |
| d |
4.31679e-09 |
3.53573e-09 |
|
With the new distributed inversion and diagonalisation subroutines the
performance and scaling of Castep was improved noticeably. As
expected, this improvement was more significant when using larger
number of cores. Figure 4.2 shows the improved
performance of Castep due to the distribution of the matrix inversion
and diagonalisation in this work package.
Figure 4.2:
Graph showing the performance and scaling improvement
achieved by the distributed inversion and diagonalisation work in Work
Package 2, compared to the straight band-parallel work from Work
Package 1. Each calculation is using 8-way band-parallelism, and
running the standard al3x3 benchmark.
|
|
The distributed diagonalisation, on top of the basic band-parallelism,
enables Castep calculations to scale effectively to between two and
four times more cores compared to Castep 4.2 (see figure
4.3). The standard al3x3 benchmark can now be
run on 1024 cores with almost 50% efficiency, which equates to over
three cores per atom, and it is expected that larger calculations will
scale better. A large demonstration calculation is being performed
that should illustrate the new Castep performance even better.
Figure 4.3:
Comparison of Castep scaling for Work Packages 1 and 2 and
the original Castep 4.2, for 10 SCF cycles of the al3x3
benchmark. Parallel efficiencies were measured relative to the 16 core
calculation with Castep 4.2.
[ num_proc_in_smp : 1]
![\includegraphics[width=1.0\textwidth]{epsimages/overall_smp1.eps}](img39.png)
[ num_proc_in_smp : 2]
![\includegraphics[width=1.0\textwidth]{epsimages/overall_smp2.eps}](img40.png)
|



Next: 5. Independent Band Optimisation
Up: castep_performance_xt
Previous: 3. Band-Parallelism (Work Package
Contents
Sarfraz A Nadeem
2008-09-03
![\includegraphics[width=1.0\textwidth]{epsimages/diag_results.eps}](img33.png)
![\includegraphics[width=1.0\textwidth]{epsimages/diag_results.eps}](img33.png)
![]() for diagonalisation of a
for diagonalisation of a ![]() matrix
scales as
matrix
scales as ![]() , so we fitted a cubic of the form
, so we fitted a cubic of the form
![\includegraphics[width=1.0\textwidth]{epsimages/phase2.eps}](img38.png)
![\includegraphics[width=1.0\textwidth]{epsimages/overall_smp1.eps}](img39.png)
![\includegraphics[width=1.0\textwidth]{epsimages/overall_smp2.eps}](img40.png)