


Next: Proposed Eigensolver
Up: Independent Band Optimisation (Work
Previous: Introduction
Contents
Castep Eigensolver
When using ultrasoft pseudopotentials, the DFT Schrödinger-like
equation becomes a generalised eigenvalue problem,
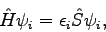 |
(6.1) |
where  and
and  are
are 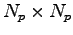 matrices in a
plane-wave basis set of
matrices in a
plane-wave basis set of 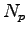 plane-waves, and we seek the lowest
plane-waves, and we seek the lowest
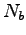 eigenstates (where
eigenstates (where 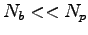 ).
).
Direct construction and diagonalisation of the Hamiltonian 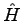 is impractical, but there are a variety of methods available to solve
for the lowest eigenstate iteratively. Typically Castep employs a
Krylov subspace method:
is impractical, but there are a variety of methods available to solve
for the lowest eigenstate iteratively. Typically Castep employs a
Krylov subspace method:
- The current (S-orthonormal) set of trial eigenstates is split
into blocks, each block spanning a small subspace and update sequentially
- For each
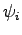 in the current block,
in the current block,
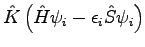 is computed (where
is computed (where 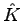 is a preconditioning matrix[2]) and added to the block subspace.
is a preconditioning matrix[2]) and added to the block subspace.
- The augmented subspace is S-orthogonalised to the existing approximate eigenstates
- The augmented subspace Hamiltonian is constructed and diagonalised, i.e. we solve
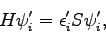 |
(6.2) |
where
- The new lowest eigenstates of the subspace are accepted as
improved approximations to the true eigenstates, and the convergence
criteria are checked. If they are not satisfied the algorithm repeats
from step 2 with further augmentations of the subspace.
It is step 3 of this algorithm that we wish to avoid,
but without it the eigenstates of each block would always tend to
converge to those of the lowest block.



Next: Proposed Eigensolver
Up: Independent Band Optimisation (Work
Previous: Introduction
Contents
Sarfraz A Nadeem
2008-09-01
![]() and
and ![]() are
are ![]() matrices in a
plane-wave basis set of
matrices in a
plane-wave basis set of ![]() plane-waves, and we seek the lowest
plane-waves, and we seek the lowest
![]() eigenstates (where
eigenstates (where ![]() ).
).
![]() is impractical, but there are a variety of methods available to solve
for the lowest eigenstate iteratively. Typically Castep employs a
Krylov subspace method:
is impractical, but there are a variety of methods available to solve
for the lowest eigenstate iteratively. Typically Castep employs a
Krylov subspace method: