Variational Monte Carlo (VMC)

VCM calculations use a trial function $\Psi(\alpha, \mathbf R,\mathbf R_I)$ whose parameters $\alpha_{ }$ are determined from the minimisation of the average energy or its variance:

$$E(\alpha)=\frac{\langle \Psi(\alpha)\vert H \vert\Psi(\alpha) \rangle} {\langle \Psi(\alpha)\vert \Psi(\alpha) \rangle} .$$ (1)

A typical trial function for an electronic system is the product between the Slater determinants of one particle orbitals (OPO), obtained from a DFT calculation, multiplied by a function that describes the particle correlations.

$$\Psi(\alpha, \mathbf R, \mathbf R_{I}) =e^{J(\alpha,\mathbf R,\mathbf R_I)}D_{\uparrow}(\mathbf r_1,\dots,\mathbf r_{N_\uparrow})$$ (2)

$$\times D_{\downarrow}(\mathbf r_{N_\uparrow+1\dots,\mathbf r_{N_e}}) ,$$ (3)

where $D_{\uparrow,\downarrow}$ are the Slater determinants of the electrons with spin up($\uparrow$) or down( $\downarrow$). The simplest Jastrow factor $J(\alpha, \mathbf R, \mathbf R_I)$ is a sum of two-electron functions

$$J(\alpha, \mathbf R, \mathbf R_I)=-\sum_{\substack{i>j \sigma_i,\sigma_j}} u_{\sigma_i,\sigma_j} (\alpha,\vert r_i-r_j\vert)$$ (4)

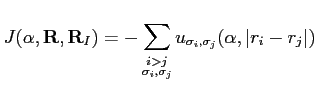where u is taken from the homogeneous electron gas. Over the years more elaborate extensions of $J(\alpha, \mathbf R, \mathbf R_I)$ have been developed in order to include three electron correlations and electron ion correlations [4].

Many studies have shown that VMC calculations recover up to $70-90\%$ of the correlation energy but the remaining contributions are hard to conquer because the results cannot be improved systematically in the VMC framework. As a matter of fact the main use of VMC calculations in CASINO is to generate the configuration set needed for the Diffusion Monte Carlo calculation.