Background

Quantum Monte Carlo(QMC) methods are accurate numerical tools used for computing the properties of physical models that contain a relatively large number of atoms, e.g.: crystals, nanoclusters or macromolecules. Although QMC computing time has the advantage of scaling with second or third powers of the system size, very precise results require the need to process large samples of phase space configurations and therefore the most challenging QMC problems require use of the most performant hardware and available algorithms  [1].

In order to set the terminology we shall briefly describe the basic mathematical concepts that provide the foundation of QMC algorithms, for a more detailed presentation we direct the reader to Refs [3,4].

A typical quantum many-body system has $N_e$ electrons with positions $\mathbf R=\{\vec r_e\}$, of which $N_{\uparrow}$ have spins up $N_\downarrow=N_e-N_\uparrow$ have spins down, and $N_I$ ions with positions $\mathbf R_I=\{\vec r_i\}$. The particle interaction is described by the quantum Hamiltonian

$$H=-\sum_{i=1,N_e}\frac{\hbar^2}{2m}\nabla_{r_i}^2+V(\mathbf R, \mathbf R_I) ,$$

from whose eigenstates and eigenvalues one can compute in principle all physical quantities describing the system. For realistic Hamiltonians exact solutions are not available but good physical results can be obtained with approximate one particle solutions, the most successful technique in this class being that of Density Functional Theory (DFT).

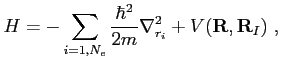QMC calculations can further improve a one particle solution by providing particle correlation contributions with the help of the following two QMC methods: