Hugo Pinto, Adam Spargo and Declan Bates
University of Exeter, UK
April, 2013
Currently, even the most sophisticated numerical models of intra-cellular phenomena consider only a single cell or population averages [1],
whereas existing agent based models (ABMs) of cell populations lack sophistication in terms of their representation of the cell [2],[3]. This is due
purely to the computational expense of combining the two approaches [4],[5]. We believe that such a combination is both desirable, and achievable
with todays massively parallel computer architectures. The aim of our research is to investigate the use of computational optimisation methods
to find the most appropriate experimental conditions for the evolution of novel multi-genetic functions in bacteria.
Traditionally, such models have been constructed using ordinary differential equations (ODEs), which are easy
to solve and often provide a good model in a continuum setting. However ODEs can model only the phenotype of a single cell, or at best model the average behaviour
over the cell population. For this reason, we developed an agent-based approach where individual
cells can exhibit variation in rates of growth and protein synthesis and mutation [6], thus allowing the representation of realistic levels of diversity.
The utility of our current serial agent-based implementation is however, limited by the number of cells which can be modelled. Limits on the memory within a single computer/node do not allow sufficient numbers of cells to be simulated to capture the diversity present in a typical laboratory culture.
Here we report the development of a parallel algorithm in order to distribute the data through the different nodes available keeping the efficiency of the serial implementation. The report is organised as follows: Section 2 model description, Section 3 MPI implementation and Section 4 validation, scalability and results. Finally the conclusions are presented in Section 5.
ABM is an agent-based implementation for the simulation of cell populations growth and is written in C. In this model, cells are allowed to grow
according to a simple metabolic model. They will initiate the replication of their chromosome at a specific mass. Once replication has terminated the two copies of the chromosome segregate to either pole and the cell divides. In modern laboratory conditions cells grow with a generation time shorter than the DNA replication time and so it is necessary to model overlapping rounds of DNA replication within a single generation. The serial implementation of ABM allows this fast growing of cells with reasonable time resolution but the maximum number of cells is limited by the available memory.
Each cell requires 12 bytes of memory thus a simulation for 1010 cells requires ![]() 100 GB of memory usually not available on a single core. A parallel implementation will allow us to fulfill such memory requirements and perform simulations with a realistic number of cells.
100 GB of memory usually not available on a single core. A parallel implementation will allow us to fulfill such memory requirements and perform simulations with a realistic number of cells.
For the parallelisation of the ABM model we used the Master-Slave approach. In this approach, one of the processes, the master,
is dedicated to perform the work distribution, while the other processes, the slaves, perform individual tasks.
Once the slave completes a task, it sends the a message to the master which also controls the flow of the algorithm.
This is the most appropriate model for distributed-memory systems.
In the parallel implementation of ABM cells grow simultaneously in the different cores. In order to assure that
cells are growing in the same condition, i.e. nutrient concentration, the common variables are updated after each time step.
The simplified algorithm for the parallel implementation of ABM is shown in Figure 1. The simulation starts with the
MPI initialisation. Then all the processes read the input file where the simulation conditions are defined, such as,
maximum number of cells, time limit, initial number of cells and growth conditions. The output file is then opened by the master process.
After the allocation of memory, the maximum number of cells are calculated and the initial cells are equally distributed through all the processes. This procedure helps the data distribution and prevents memory usage imbalance.
In each time step all the processes grow cells independently. In the end the substrate is updated to ensure that all the processes are performing the simulation in the same conditions. At the end of each iteration the output is written by the master process. The simulation stops when one of the processes reaches the maximum number of cells or the time limit allowed for the simulation.
In order to validate the parallel implementation a simulation with a time limit of 1000 steps, using 1 GB of memory and 1024 initial cells was performed and the results compared with the ones obtained with the serial implementation. To ensure that both calculations were performed in the same conditions the random numbers were replaced by parameters. All calculations were performed on the Zen cluster at the University of Exeter, with the following hardware specifications:
The serial implementation was compiled using both gcc 4.6.3 and Intel icc 12.1 with -O2 level optimisation. The two compilers gave almost identical timings. The parallel implementation was compiled with the Intel MPI Library version 4.0 and icc 12.1, again with -O2 level optimisation.
Both calculations lead to the same total number of cells and more important the number of cells at each time step was exactly the same. The evolution of the substrate was also monitored and minor differences were found for calculation using a different number of cores. This can be attributed to numerical errors introduced by the function MPI_Allreduce used to sum the nutrient concentration to be updated after each time step. However this numerical instability can be ignored since it does not have any consequence in the evolution of the cells growth.
One of the most important studies for a parallel implementation is to understand how the code scales with the number of cores used. If the communication time
between the master and the slaves is small compared with task execution, the model should scale well in the limit of a large number of tasks. Otherwise there is an imbalance in the workload making the parallelisation inefficient.
In order to investigate the scalability of ABM two simulations were performed using 1 and 10 GB of memory. Since the number of cells we can simulate with 1 GB is small we expect that the communication time will dominate (poor scalability) while for the 10 GB calculation the execution of tasks is expected to dominate (good scalability). Thus, for the 1 GB simulation we used 1, 4, 8 and 12 cores while for the 10 GB we used 12, 16, 20 and 24 cores.
a)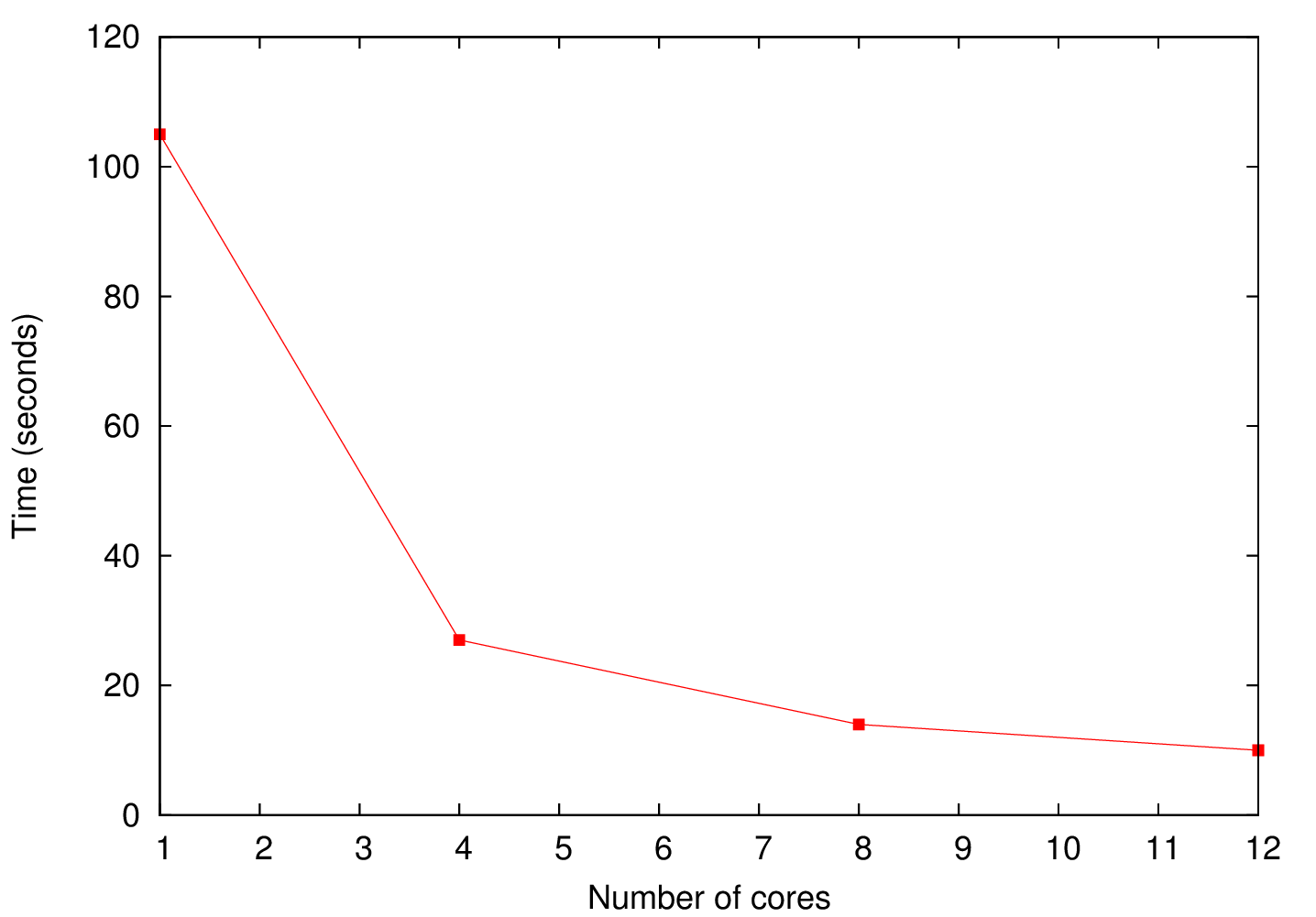 b)
b)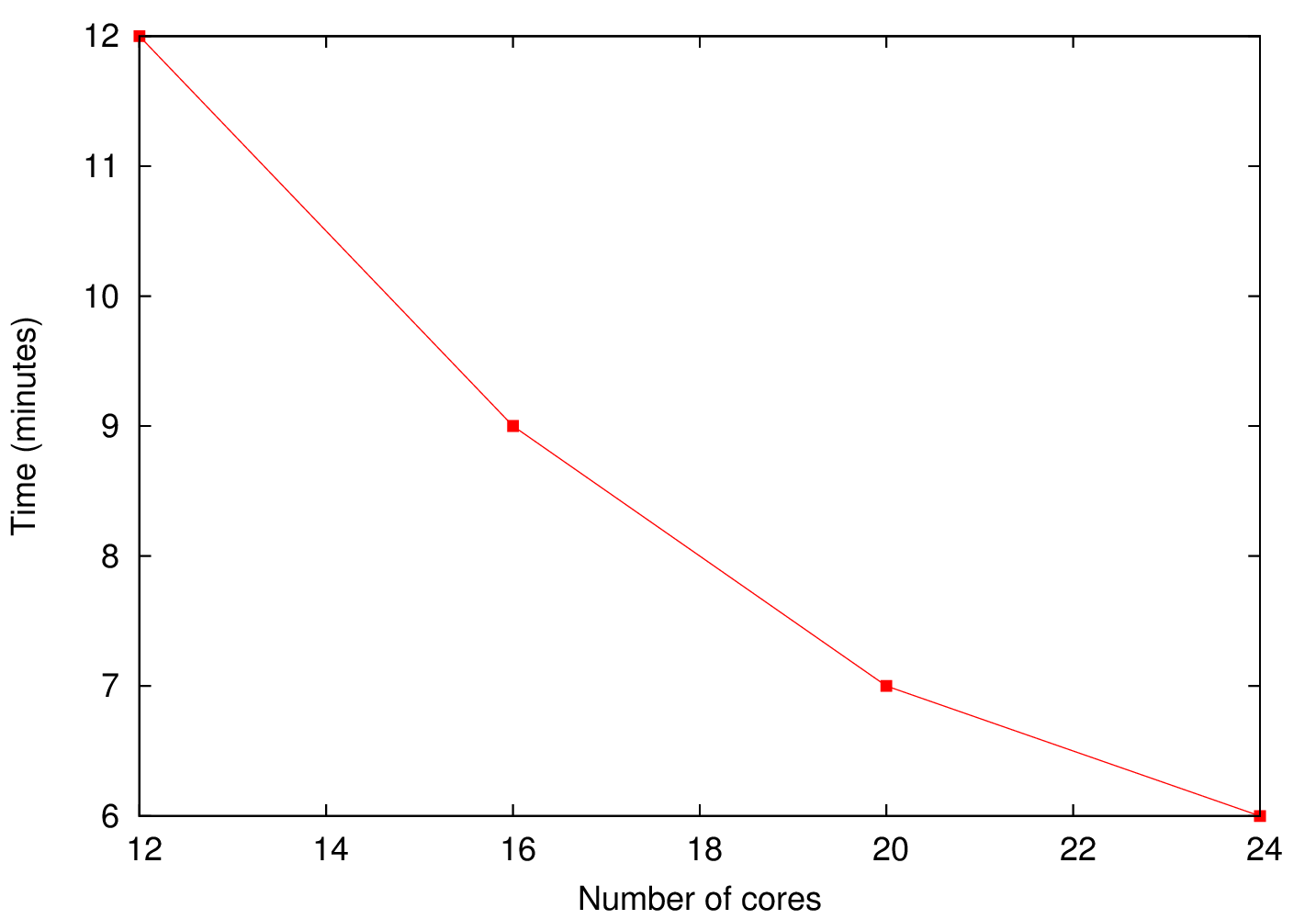 |
Figure 2 a) shows the execution time as a function of the number of processes used for the 1 GB simulation. As it was expected, since the number of cells is relatively low the signalling between the master and the slaves dominates which makes the scalability poor. In the case of the 10 GB the number of cells is large enough in order to make the task execution dominant over the communication. Figure 2 b) shows that the execution time as a function of the number of processes used is almost linear suggestion a good scalability of the code.
a)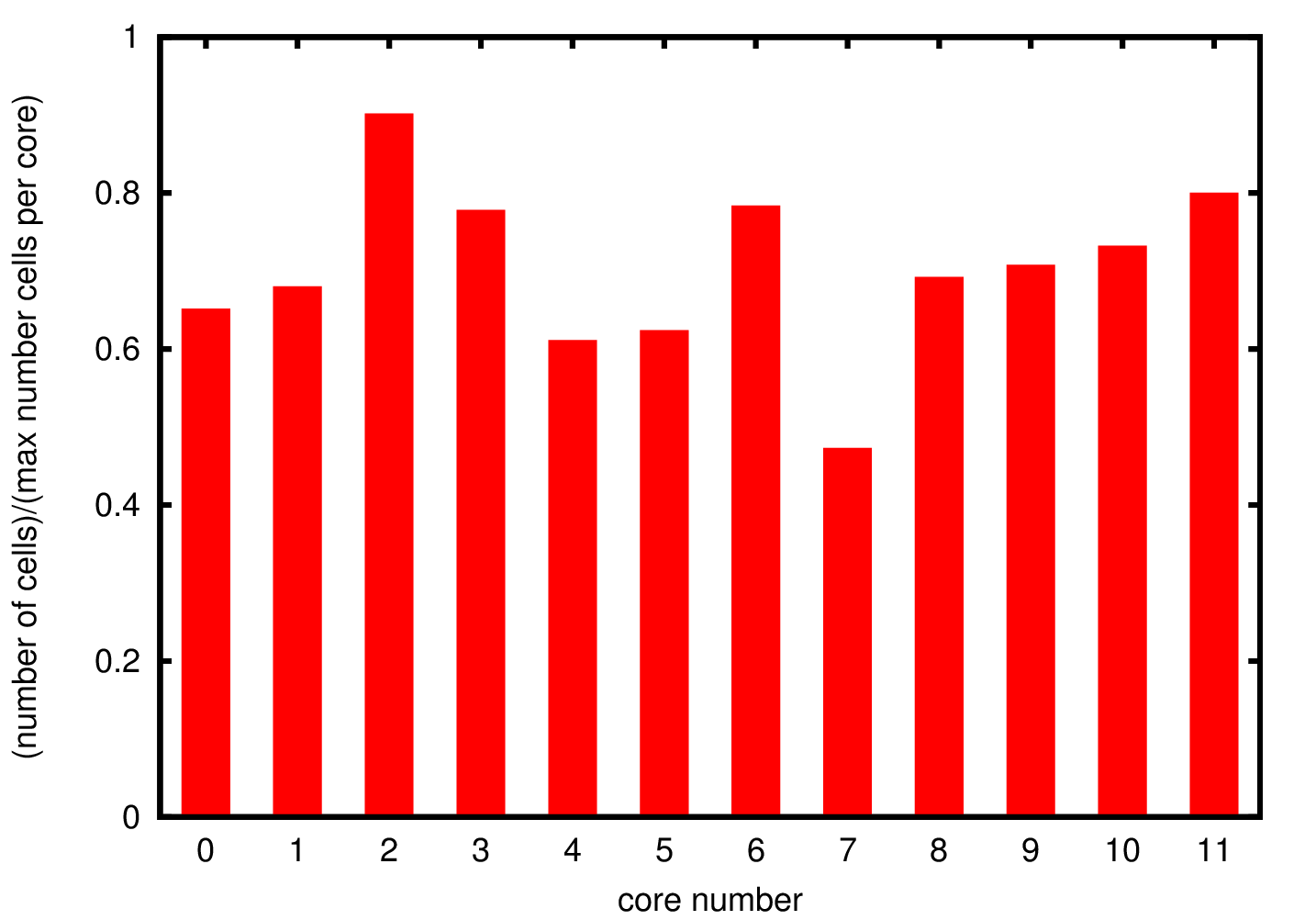 b)
b)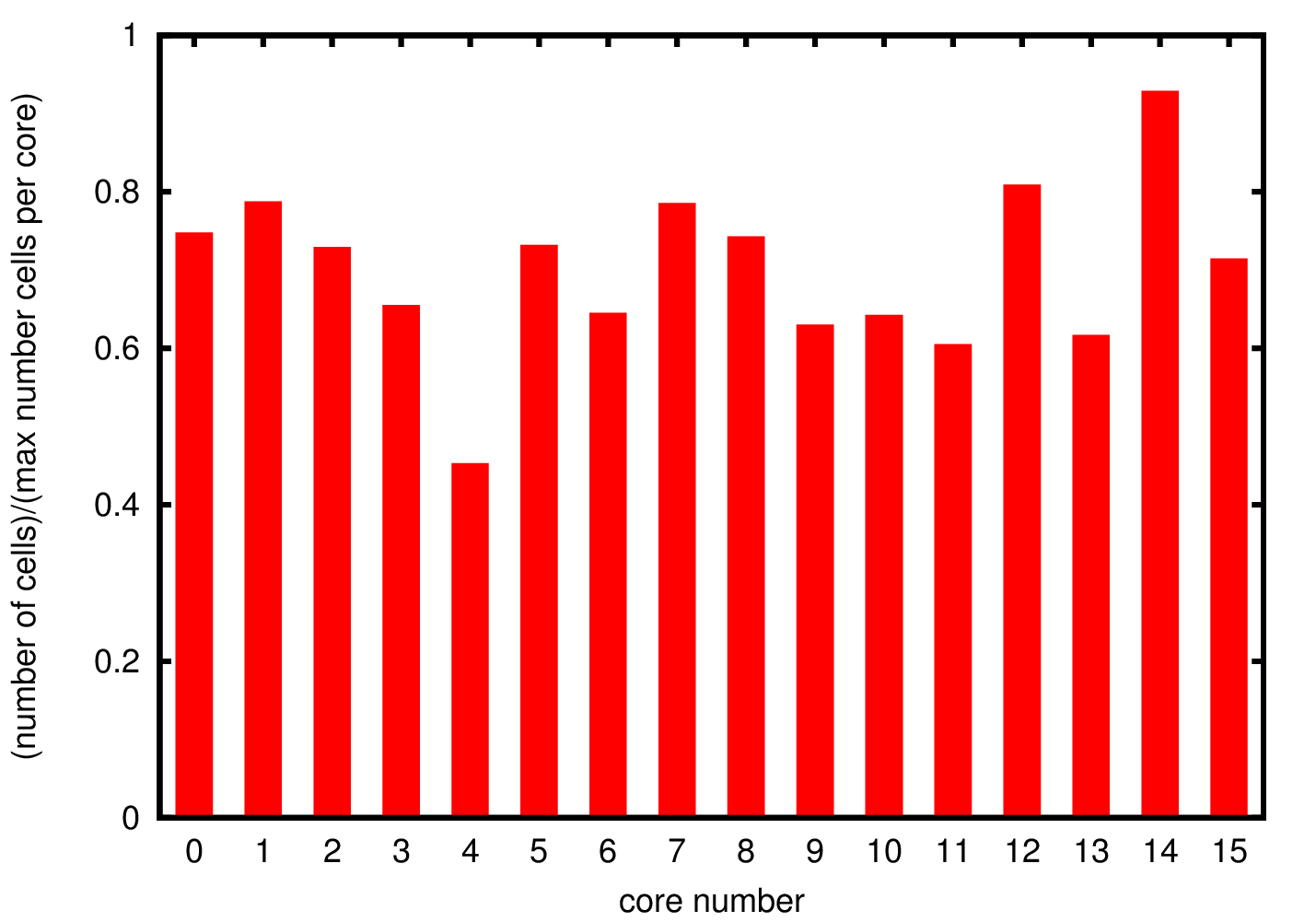
c) 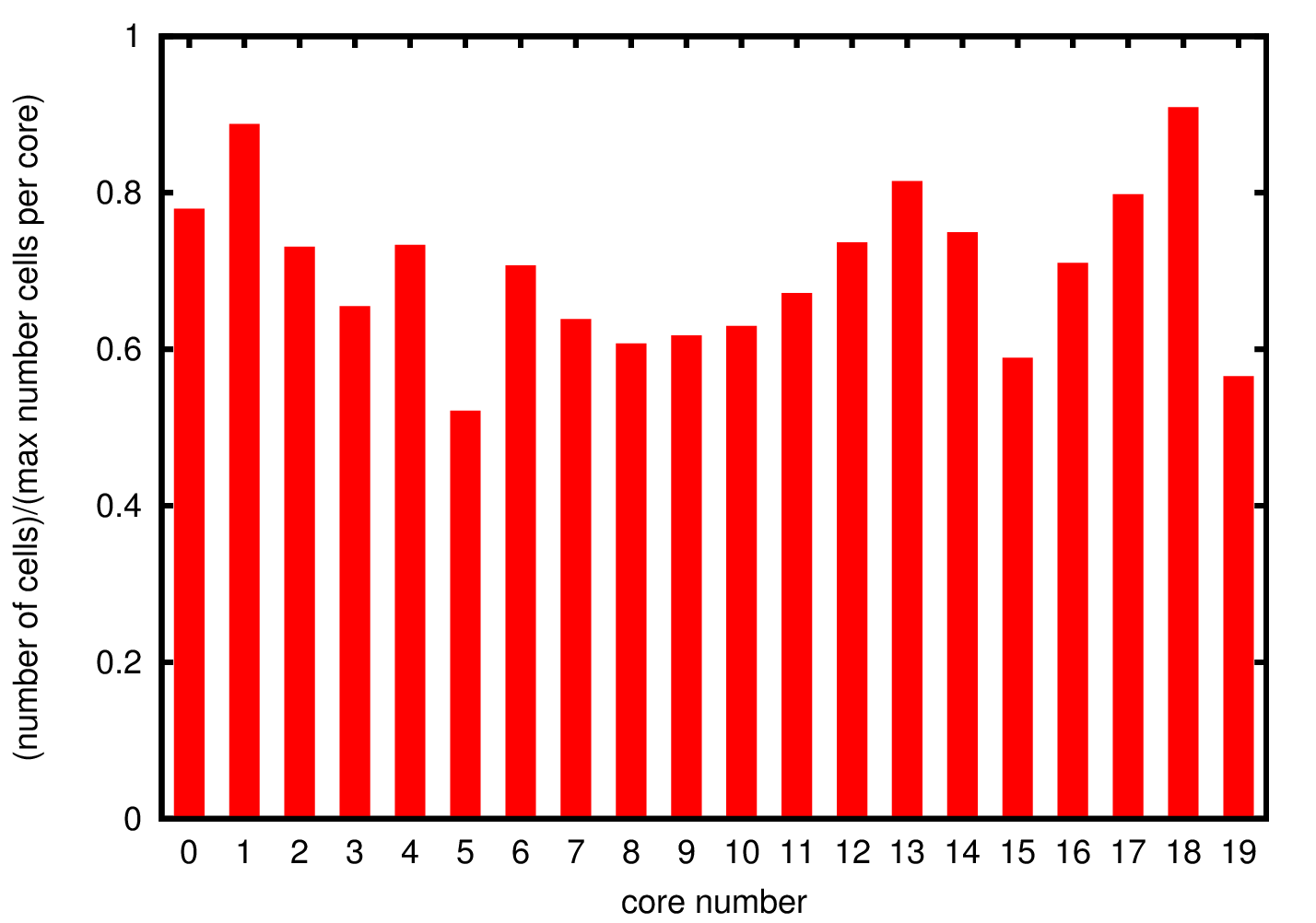 d)
d)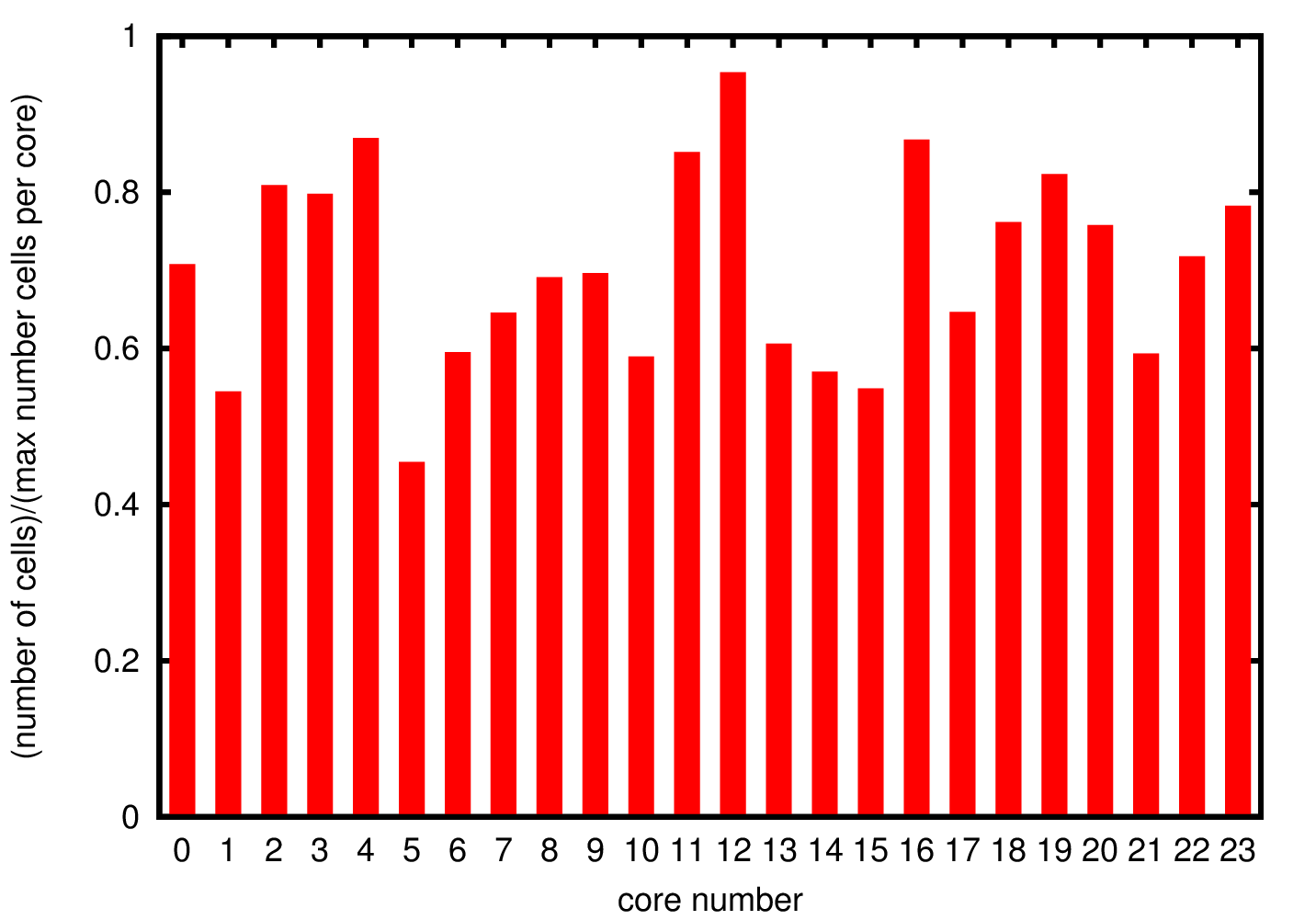 |
Since there is no data distribution during the simulation, i.e. there is no exchange of cells between the different processes, if a process is growing cells at a faster rate than the others the simulations will stop before it is completed. For this reason it is important to understand the cells distribution through the different processes to ensure that the distribution of data is uniform.
In Figure 3 we show the cell distribution over the different cores. The average memory usage is approximately 70% of the allocated memory. Due to the randomness in the cells growth the total number of cells is not exactly the same but there are not significant deviations suggesting uniform growth in the different processes.
With the parallelised version of ABM the computational resources required for a realistic simulation can be achieved. Using as input the initial number of cells and the growth rate measured experimentally a simulation for the growth of cells was performed. For this calculation 96 GB of memory was required, distributed over 4 nodes and 48 processors. The results were compared with the experiment. Figure 4 shows the comparison between the measured (squares) and calculated (line) cells as a function of time. The y-axes is set to log scale base 2.
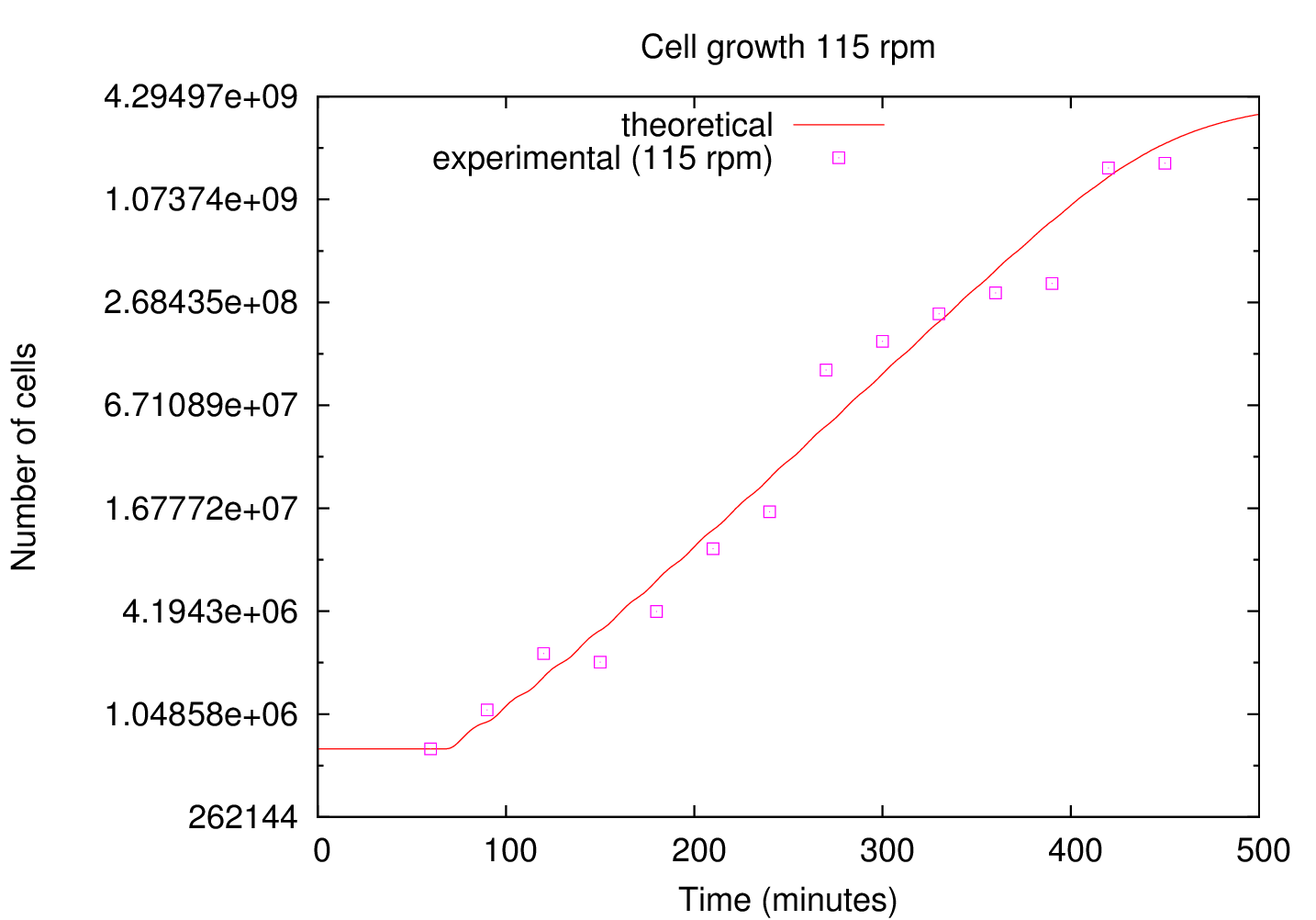 |
The calculated number of cells is in good agreement with the measured numbered of cells. After the lag phase (t![]() 60 min) the number of cells grows exponentially until the substrate runs out of nutrients (t
60 min) the number of cells grows exponentially until the substrate runs out of nutrients (t![]() 400 min).
The ABM model is now an important tool to help with the understanding of the underlying mechanisms involved in cell growth. The fact that the code can perform
a real scale simulation in a very short time (approximately 10 min) using only 4 nodes gives the opportunity to include further complexity to the model.
400 min).
The ABM model is now an important tool to help with the understanding of the underlying mechanisms involved in cell growth. The fact that the code can perform
a real scale simulation in a very short time (approximately 10 min) using only 4 nodes gives the opportunity to include further complexity to the model.
An MPI parallel version of the ABM model was successfully implemented. Using the same input, the calculations performed with the parallel implementation are in perfect agreement with the ones performed with the serial implementation. The parallel version of the code allowed us to perform calculations with the amount of memory required to simulate real systems. For such calculations the run time scales linearly with respect to the number of cores used. A simulation of 1010 cells can be performed in about 10 minutes using 4 nodes (48 cores) which implies that further complexity can be added to the model.
This project was funded under the HECToR Distributed Computational Science and Engineering (CSE) Service operated by NAG Ltd. HECToR - A Research Councils UK High End Computing Service - is the UK's national supercomputing service, managed by EPSRC on behalf of the participating Research Councils. Its mission is to support capability science and engineering in UK academia. The HECToR supercomputers are managed by UoE HPCx Ltd and the CSE Support Service is provided by NAG Ltd. http://www.hector.ac.uk
This document was generated using the LaTeX2HTML translator Version 2008 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -no-navigation -show_section_numbers -html_version 3.2,math -no-math -local_icons -antialias index
The translation was initiated on 2013-04-22