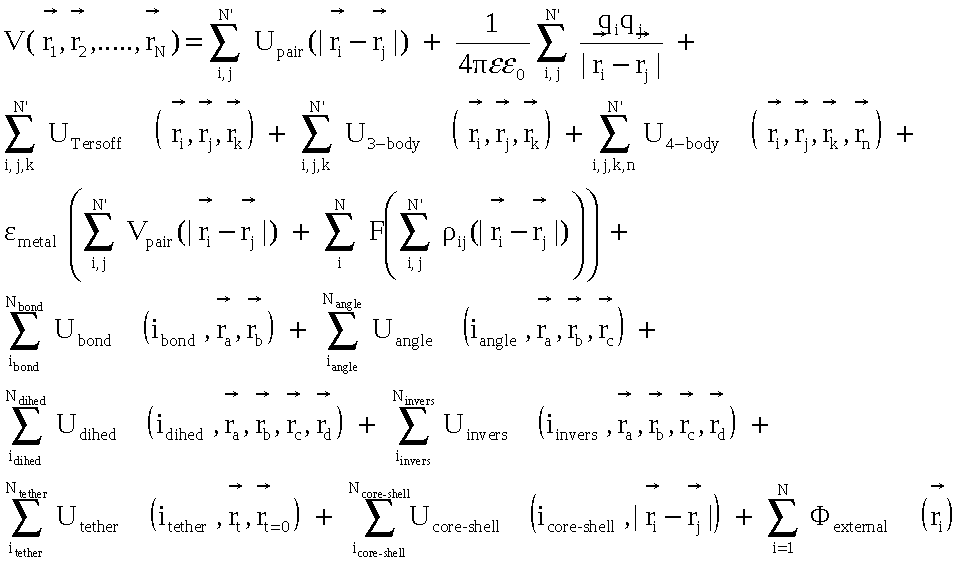
Table of Contents
2 Work Package 1: Implementing a Mixed Mode DL_POLY_4 2
Assignment of Atoms to the Link Cells and Calculation of the Verlet Neighbour List 2
The evaluation of the force terms 4
3 Work Package 2: Enabling Billion Atom Simulations 12
DL_POLY_4i is a general purpose classical Molecular Dynamics (MD) simulation software package which has been developed at STFC Daresbury Laboratoryii by I.T. Todorov and W. Smith. The package is used to model the atomistic evolution of the full spectrum of models commonly employed in the materials science, solid state chemistry, biological simulation and soft condensed-matter communities. It has been developed under the auspices of CCP5iii and is widely used throughout the UK as well as world-wide. It is a fully data distributed code, employing methodologies such as spatial domain decomposition , link-cells, Verlet neighbourlistiv and the 3D Daresbury Fourier Transform (DaFT)v. The code demonstrates excellent performance and has been shown to scale to large numbers of processors.
The purpose of this dCSE project is to markedly increase not only the number of cores that can be used efficiently by DL_POLY_4 but also the system sizes that it can be used to study. The first of these aims has been achieved by the introduction of a second level of parallelism using OpenMP, so circumventing a limitation of the link cell approach. This is covered in section 2. The system size issues result from DL_POLY_4 using default 32 bit integers throughout, and so the second part of the project has introduced 64 bit integers into DL_POLY_4 where appropriate, thus making the maximum system size well beyond that which can be currently studied on HPC architectures. This is described in section 3.
As stated above the linked cells algorithmvi is the basis upon which DL_POLY_4 is parallelised, which it achieves by using an equispatial domain decomposition. The simulation cell is divided into a number of equal volume, isomorphic, parallelipiped domains, and each domain is assigned to an MPI process. As most inter-atomic interactions become negligible beyond a finite distance, the “cut off”, only position data for atoms near the edges of each domain need communicating to neighbouring cores for the atomic interactions to be calculated, provided the cut off is much smaller than the length of the edge of the domains. The link cell method thus has much in common with the halo exchange methods used in solving differential equations on grids, except that it is generalised to allow for the “grid points”, i.e. the atoms, to be disordered in space, and for them to move from time step to time step.
However, as the number of MPI processes is increased the link cell algorithm begins to show its limitations. Many MPI processes result in small domains, and for the algorithm to work at all the sides of the domains must be larger than the cut off. In fact for some simulations, especially those with inter-atomic potentials that require large cut offs, this breakdown of the link cell algorithm is ultimately the limit on the number of cores that can be used, despite the simulation still scaling well at the point the breakdown occurs. However, if this breakdown occurs at P processes were it also possible to employ T threads, as it would be in a mixed mode code, it is clear that T*P cores in total can now be exploited. Thus provided a second level of parallelism based upon threads can be introduced and if it is efficient it will allow the scientist studying such problems to immediately be able to exploit up to an order of magnitude more cores (given current multicore architectures), a situation of particular benefit to those who wish to study phenomena that have relatively short length but extremely long time scales. A second point is that the cost of the calculation is roughly proportional to the size of the cut off cubed, and so in the case of potentials with large cut offs it is again clear that the ability to use a second level of parallelism to enable more cores to be used will be extremely beneficial.
The implementation of an extra level of parallelism into DL_POLY_4 is in principle quite straightforward. The link cell algorithm provides the domain decomposition of the problem, so at least to zeroth order one may ignore the MPI framework and the main issues to address are
The assignment of the atoms to the link cells and the evaluation of the Verlet neighbour list
The evaluation of the various different force terms
We shall describe the implementation in this order before returning to the issue of the MPI framework and whether it can be improved by the use of threads.
In the link cell algorithm the unit cell is broken down into a number of small parallelepipeds with sides of length as close as possible to the cut off. Each of these parallelepipeds is called a Link Cell. This means that an atom only interacts with atoms in its own link cell or its neighbours. To run this model on many processes it is then a simple matter of assigning an equal number of link cells to each process. To minimise the amount of communications this is best done by assigning a volume of space to each process, and hence all the link cells in that space, and the nett result is similar to that found for many parallel PDE solvers: The work required to evaluate the forces is proportional to the volume of the domain, since that is proportional to the number of atoms contained, while the communications are proportional to surface area, and it is the ratio of the two quantities that determine the parallel scaling.
Thus the link cell algorithm accelerates the evaluation of the inter-atomic forces by massively reducing the space that must be searched for atoms when calculating interactions. DL_POLY_4 takes this one step further by also calculating a Verlet Neighbour Listvii. This is simply to list for each atom explicitly which other atoms it can interact with due to them being within the cut off, a calculation that is massively accelerated by the use of the the link cell method. That such a list can make a marked saving over and above the link cell method may seem surprising, but if one considers the volume of a sphere inscribed in a cube one sees that the ratio of volumes is approximately 1.9 so one can hope for a saving of a factor of roughly 2 in each of the force terms by this method.
The use of link cells and Verlet neighbour lists is both highly efficient, reducing the scaling of the calculation of the forces from in principle O(N2) to O(N), and also a victim of its own success; the calculation of the forces is now so quick that the assignment of the atoms to the link cells and the evaluation of the neighbour list becomes an appreciable proportion of the run time! In some cases we have observed the routines involved taking up to 30% of the run time. As such
If we propose to speed up the evaluation of the forces by the use of OpenMP threads we must also address this portion of the code
A second dCSE project has been submitted and accepted to incorporate algorithmic improvements in this portion of the code.
The parallelisation of the evaluation of the neighbour list is straightforward; each neighbour list is independent of any of the others, and so each thread can evaluate the neighbour list for a different set of atoms. The assignment of the atoms to link cells is, however, a little more complicated. The serial method is
For each atom in turn
Evaluate which cell the atom is in
Add the atom to the end of list for that cell
The last of these steps requires care if shared memory parallelism is being employed due to the potential race condition that may occur when more than 1 thread is trying to add to the end of a given list. A number of methods to work around this were tried, but by far the most effective was found to be to let each thread built up its own list independently and then merge the lists rather than to introduce synchronisation points directly into the serial method. While fairly simple to solve it does point to one issue that occurred a number of times through the project – while the link cell algorithm and subsequent decomposition by domains results in a structure that does, in some ways, remind one of solving PDEs on a regular grid, the fact that the atoms do move and that density fluctuations, however slight, will occur means that unlike the regular grid case where the points are static one can never know which atoms neighbour one another at a given point in time, or even simply how many atoms are in a given region of space. This means that at a number of places in the code similar lists must be built, thus introducing an overhead in the threaded code when compared to the serial.
The general from of the force field supported by DL_POLY can be given as
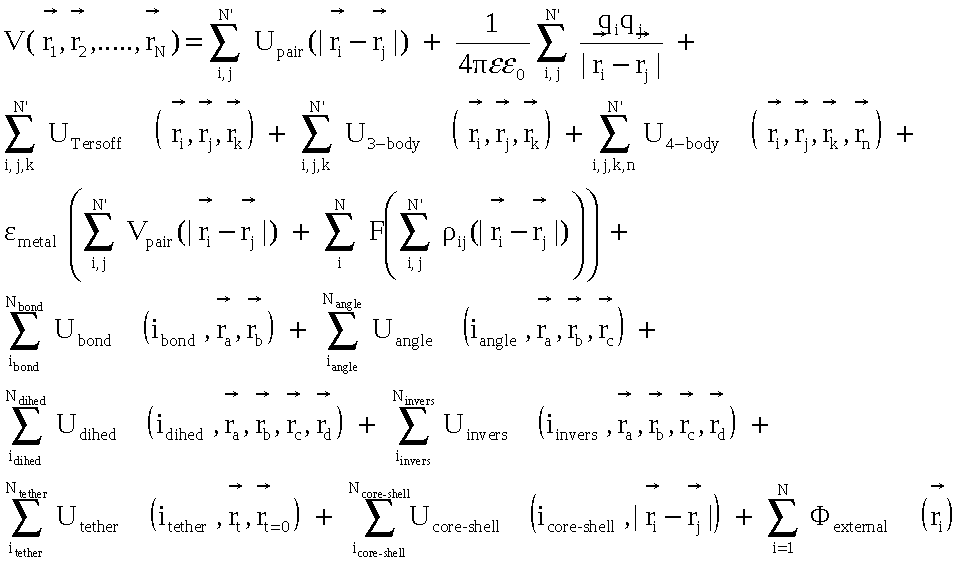
where the potential energy of the system is written as a function of the coordinates of all the species comprising the system. From this it can be seen that the main issue of parallelising the evaluation of the force terms is simply the number of terms in the expansion!
In fact the majority of the terms are simply loops over independent entities, often, but not always, atoms, which can easily be parallelised provided one is careful to correctly state that energy, forces, stresses and related quantities need to be reduced across the threads at the end of the loops. Thus these terms are fairly straightforward, though in practice the use of static variables by the code, OpenMP 2's non-existent mechanisms for error handling in parallel regions and simply the sheer number of variables that needed scoping in a parallel region meant the work required a large amount of care.
However a small number of routines do not fit this structure, and as such needed to be handled differently. In particular these included
The long range component of the Ewald Forces
And forces due to constraints on the atoms
It is also convenient here to consider the communication routines that reform the halo at the end of each timestep.
DLPOLY_4 uses the SPMEviii variant of the Ewald method to evaluate the Coulomb forces between atoms. As one component of these interactions is long ranged they do not fit into the link cell method outlined above, and instead a Fourier space based method is used. This requires the following main steps
Evaluate (a quantity related to) the charge density of the atoms on a regular grid in real space
Fourier transform that grid to Fourier space
Convolve the result of step 2 with the Fourier space representation of the Ewald potential
Inverse Fourier transform the result back to real space
Calculate the energy, stresses, and forces on the atoms using the result from step 4
Steps 3 and 5 require loops over independent quantities, grid points and atoms respectively, and so fit into the recipe described above. However a number of different methods were investigated for step 1, and the DaFTix routines used for the FFT by DL_POLY_4 needed to be parallelised with OpenMP.
The evaluation of the charge density on the grid is simple in principle: Loop over all atoms that can contribute to the charge density in the domain of interest and for each atom add their contribution to the appropriate grid points. Thus to parallelise using OpenMP the easiest method is to have each thread evaluate the charge density for a different subset of the atoms being careful to synchronise appropriately to avoid race conditions when two different atoms contribute to the same grid point. We considered 3 different methods for this synchronisation, namely a reduction on the grid at the end of the loops, and using either atomic or critical to protect the addition. We expected to find that the reduction was the best performing. However as the grid is, in memory terms, a very expensive object we wished to examine whether the other methods were viable as we expected using a reduction would require each thread to have a private copy of the grid. In practice the performance overheads for using either atomic or critical were found to be totally unacceptable, and the final version uses a reduction despite the potential memory issues.
The FFT as implemented by DaFT has two main steps
A set of serial 1D FFTs on the local data
Combining the data held by two different MPI processes. This requires a communication stage and also the application of a set of complex “twiddle factors”
The first step was parallelised by changing the 1D FFT routines used by the code from GPFA, a commonly used set of FFT routines implemented by Clive Tempertonx, to the routines in ACMLxi. These were chosen not only because they are threaded but also because they offer high performance solutions on a wide variety of HPC architectures without having a licence that would place undue restrictions on the use of DL_POLY_4.
Two methods were investigated for step 2. They are closely related in that the thread parallelism is over the vectors in the x, y or z direction (depending on the stage of the 3D transform) but in one synchronous communications were used, while in the other it was attempted to overlap the communications stage with the computation by having 1 of the threads performing the communication while the others worked. In practice no gain was found for the second method, and for reasons of code simplicity the first method is the one used in the final implementation.
One way DL_POLY_4 supports species with chemical bonds is by the use of constraints: Two atoms are constrained to always be separated by constant distance. This is implemented by the SHAKExii (and where appropriate RATTLExiii) algorithms. In these the atoms are initially moved without including the effect of the constraints, and then the non-linear constraint equations are solved iteratively by a Gauss-Siedel method to move the atoms back to the correct separation. Thus each constraint affects the position of two atoms. Further it is easy to see that a given atom may have more than one constraint acting upon it; for instance consider modelling water using constraints, at the simplest level it is clear that the oxygen atom will have two constraints, one for each of the hydrogen atoms.
The way DL_POLY_4 is structured means that the simplest way to parallelise the SHAKE routines is over the constraints. However the above discussion shows clearly that as the position of a given atom can be affected by more than one constraint there is the possibility of race conditions when performing this update. A number of methods were investigated to avoid this, and in practice an atomic directive was found to be the most effective of the ones tried, though it does introduce a degree of synchronisation between the threads.
In fact it is possible to restructure the SHAKE and RATTLE routines such that they can be parallelised over atoms so avoid this synchronisation. However this would require a fairly major rewriting of this section of DL_POLY_4 and there was insufficient time to attempt it.
Similar to solving PDEs on a regular grid at the end of each time step it is necessary for DL_POLY_4 to communicate data so that the information held by a given process is correctly updated. In the case of DL_POLY_4 this includes not just updating the halo for a given processes domain, but also the domain itself as the whole point of the program is that the atoms can move!
In the case of PDEs it has been shown that in a mixed MPI/OpenMP program quite substantial performance gains can be achieved by using the threads to overlap the communication and computation. An example is given in figure 1. This shows the speed up for the solution of the 2-D Poisson equation, and it can be seen that almost linear speed up can be achieved if communications and communications are overlapped (cco).
It was hoped that similar effects could be achieved for DL_POLY_4, but in practice this proved difficult within the current framework. Ultimately the situation is similar to that found when building the link cells in parallel using threads. Again, unlike the regular grid, we do not know a priori which atoms needed to be communicated, thus making it difficult to overlap the communication with computation, and also meaning that lists of atoms and their associated data need to be generated before the communication can occur thus incurring the parallel overhead noted before. In fact in this case the overhead due to synchronisation is worse as at least in the case of the link cells all atoms in the domain are involved, while here we are only dealing with the small subset that need to be communicated.
A number of attempts were made to efficiently parallelise the communication stage, for instance once the communication buffer has reached a certain size it is possible for one thread to start sending it while the other start building the next buffer. In each case it was found that the original method was more efficient, and in the final code while the parallel communications are available and may be turned on by the user, by default the serial method is used. However the experience developed here has been built into the more recent dCSE proposal for improving the communications within the code which addresses in a more general way the communications within the code.
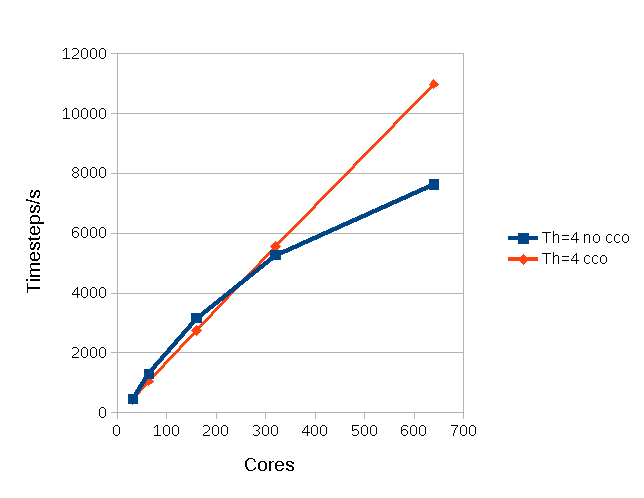
Figure
1: Performance of a 2D Laplace equation solver
In this section we shall review some performance results for the mixed OpenMP/MPI code. In all the graphs the cores axis to the total number of cores used, NOT the number of MPI processes. Thus 256 cores could mean 256 MPI processes all single threaded, or 128 process each with 2 threads etc. In all cases all nodes are fully populated. All results presented are from an executable generated by the GNU compiler suite (version 4.4 or later), but the code has also been run on HECToR with the Cray compiler, and limited testing has occurred on other machines with the Intel and Sun compilers.
In Figure 2 are results from HECToR for the simulation of one of the simplest possible systems for MD, liquid Argon. The force field only uses Van der Waals terms, which are modelled by a simple Lennard-Jones 12-6 potential. The systems consists of 256,000 atoms, the unit cell is a cube with side 210.36Å and a cut off of 9Å is used.
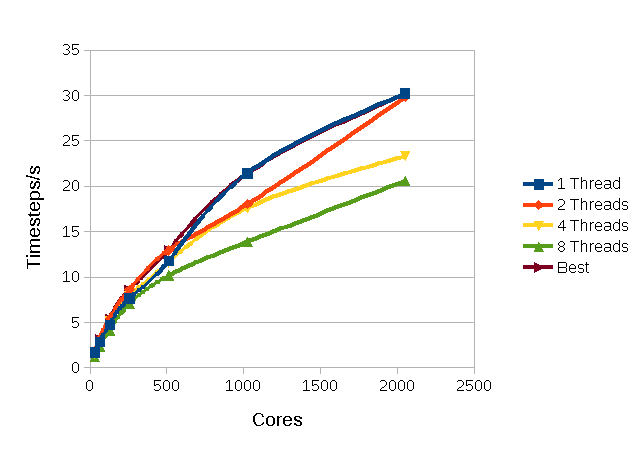
Figure
2: Performance For Argon with a 9Å
cut off
Figure 3 shows the same system except with a cut off of 15Å.
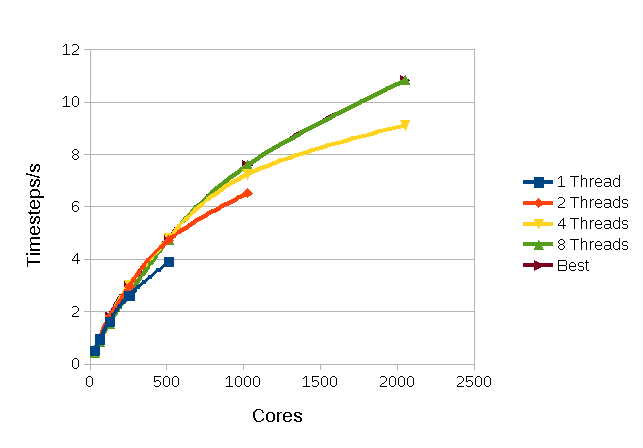
Figure
3: Performance For Argon with a 15Å
cut off
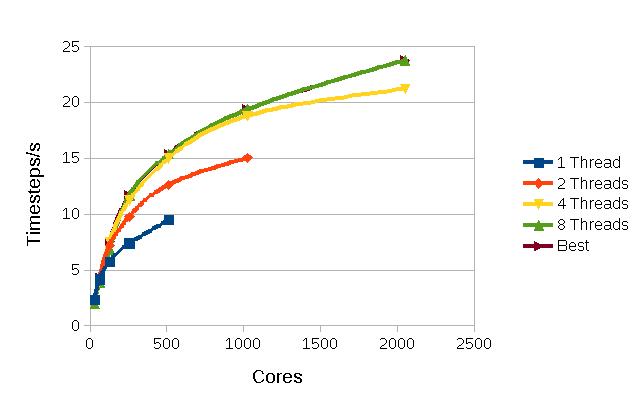
Figure
4: Performance for a Sodium/Potassium Disilicate Glass
The final example in figure 5 is the biological molecule Gramicidin-A in water. This is a polypeptide that displays antibiotic behaviour. The simulation contains 99120 atoms in total and has a cut off of 8Å. The unit cell is tetragonal with a=94.6Å and c=112.7Å. The force field is more complex again, and includes not only the terms considered above, but also terms involving bonds, modelled both as constrained separations (for the water molecules) and as springs (within the Gramicidin molecule), and terms depending on bond angles and also dihedral (torsional) angles.
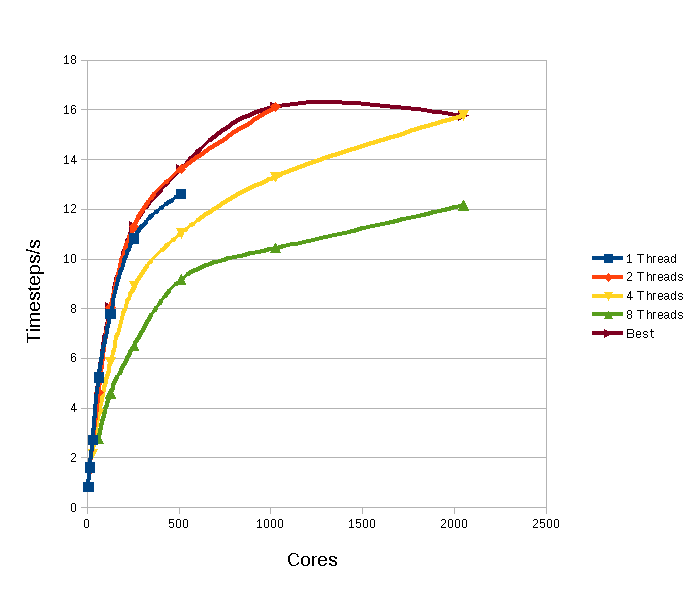
Figure
5: Performance for Gramicidin-A in Water
|
Threads |
Time/s |
|
1 |
6.64 |
|
2 |
4.81 |
|
4 |
4.10 |
|
8 |
3.67 |
Table 1: The scaling of the constraint routines
The effect of the synchronization introduced by the atomic directives is clear, and should time be available it would be hoped that restructuring of the SHAKE routines to better exploit thread parallelism would result in scaling with thread number that is closer to the disilicate glass case.
Thus while threads are generally beneficial quite what is the best combination of threads and processes is force field (and computational system) dependent. In practice to get the best out of the code it will be necessary for the user to experiment with a few short runs to find the best combination, but as experience is gained with the mixed mode code we will document findings to help guide them in this choice. In fact this is much the same as the pure MPI code!
The code including the changes described above is currently in an experimental branch of the DL_POLY repository at CCPForge, and the plan is to merge it in the near future with the main branch and release to users.
It can be clearly seen from the above examples that the use of threads can both increase the number of cores that DL_POLY can exploit and also increase the performance. In some cases, such as the glass presented above, this can be a very marked increase in both quantities. However what can be achieved does depend upon the form of the force field being employed by the simulation, but it does seem that the use of threads can definitely improve what DL_POLY is capable of, especially close to the “MPI limit.”
The largest simulations currently performed by DL_POLY_4 are of the order of 500 million particles. These are used to examine the damage in materials that occurs due to the recoil of a radioactive nucleus when it decays. Due to the extremely high energies involved in nuclear processes this can affect very large areas within the material, and thus the simulation requires extremely large cells and consequently large numbers of atoms. However, even with the current numbers of atoms employed in the simulation the simulated volume is still not large enough to hold a real high energy recoil, let alone multiple and overlapping recoils to simulate realistic damage events. Therefore, it is desirable to use somewhat larger systems, but this runs into a simple yet frustrating computational limit within the code, that default 32-bit integers are used throughout, and the largest (positive) integer that these can represent is about 231=2,147,483,648, only a factor of 4 bigger than simulations that are currently being performed.
Thus to future proof the code any integer that represents a global index needs to be changed to a longer integer kind. Given that the latest Fortran standard, Fortran 2008, specifies that integers in the range +/-1018 must be supportedxiv and that these integers are all but universally supported by Fortran compilersxv it was proposed to introduce this integer kind into the code to be used for all variables that may hold the global indices.
These global indices are used where it is necessary to identify a specific atom within the run. A simple example is on output, it is necessary to define a quantity for each atom so that we can, for instance, follow the motion of a given atom. However internally there are a number of other tables that are used to define the connectivity of the species being simulated – when calculating the forces associated with a water molecule it is not enough to know that the oxygen atom is bonded to 2 hydrogen atoms, one must know exactly which hydrogen atoms out of all those within the simulation. Thus global indices permeate much of the code, and it proved necessary to go through the code very carefully to identify exactly what required promotion and what could be left as 32 bit. For this portion of the work we are extremely indebted to Dr Ilian Todorov, author of DL_POLY_4, for his help in a number of unclear situations. In fact due to these discussions the resultant code is somewhat clearer than the original, especially where variables were being used to hold both local and global indices at different parts in the code.
Thus the work, while not difficult, did require painstaking care, though use of NAG compiler version 5.3.1 and later which can detect integer overflow did help on occasion. We should also stress again, as said in the proposal, that simply promoting all integers in the code was not an appropriate solution. The main reason for this is that the largest data structure in the code, the Verlet Neighbour list mentioned above, requires only local indices and can thus be perfectly adequately represented with 32 bit kinds. Promoting to 64 bits could nearly double the memory usage of the code, and in a world with decreasing memory per core this is simply not acceptable.
Testing the 64 bit code proved difficult as the runs on the largest systems are only just possible on HECToR, in each case at least half the machine had to be used. In fact in some cases we had to artificially reduce cut offs to perform the runs, and thus the runs may not be very accurate. However they are enough to test the molecular dynamics portion of the code. That said it must be admitted that simply due to disk space considerations we had to turn off much of the I/O of the code, and thus that part of a run has not been tested as well as we would like.
We should also note that progress in certain places was not as swift as one might like due to bugs when dealing with 64 bit integers in the MPI library on HECToR. For instance the routine MPI_TYPE_CREATE_F90_INTEGER should return a handle to a MPI integer type with requested range that can be used in subsequent communications. In practice we found that while a handle was returned subsequent communications failed on HECToR with the MPI library claiming the type did no exist. Therefore we had to work around this by using MPI_INTEGER8 though strictly the MPI standard does not require that this is supported.
3 series of runs were performed, on Argon (with a markedly reduced cut off) to check the basic code, Sodium Chloride to check the non-bonded terms (with slightly reduced Ewald tolerances) and Water to check the bonded terms (again slightly reduced Ewald tolerances). In each case the method used to verify that the run was correct was to scale the system up from a small size and check that that the energy per particle was constant within the expected tolerances. As before the GNU compiler suite has been used to generate the results.
The results of the Argon runs are shown in table 2
|
Number Of Particles |
Number/231 |
Total Energy |
Total Energy/Particle |
|
2048000 |
0.0009536743 |
379597287015.312 |
185350.237800445 |
|
16384000 |
0.0076293945 |
3036778296122.86 |
185350.237800468 |
|
131072000 |
0.0610351563 |
24294226368983.3 |
185350.237800471 |
|
1048576000 |
0.48828125 |
194353810951866 |
185350.23780047 |
|
4294967296 |
2 |
796073209658845 |
185350.237800471 |
Table 2; Argon
It can be seen that the energy per particle is extremely well conserved thus providing good evidence of the correctness of the code. Out of interest in the largest case the side of the cubic simulation cell is 539nm, or roughly the wavelength of visible light.
The results for NaCl are shown in table 3
|
Number Of Particles |
Number/231 |
Total Energy |
Total Energy/Particle |
|
4096000 |
0.0019073486 |
-159282467501.217 |
-38887.3211672893 |
|
32768000 |
0.0152587891 |
-1274643765558.87 |
-38899.040696987 |
|
262144000 |
0.1220703125 |
-10197290041763 |
-38899.5744390984 |
|
2097152000 |
0.9765625 |
-81566710329911.9 |
-38894.0383576927 |
|
4298942376 |
2.0018510409 |
-167173602476120 |
-38887.1466175987 |
Table 3: NaCl
It can be seen that while roughly consistent the energy per particle shows much more variation than for the Argon case. In fact the tolerances used for the Ewald summation should lead to variation in roughly the 5th significant figure, which is what is observed, so again these results support the code being correct
Finally in table 4 are the results for the simulations of water
|
Number Of Particles |
Number/231 |
Total Energy |
Total Energy/Particle |
|
768 |
3.576278686*10-7 |
-2484.9971734628 |
-3.2356734029 |
|
52931328 |
0.0246480703 |
-171254197.138575 |
-3.2354033728 |
|
578742528 |
0.2694979906 |
-1872529167.86996 |
-3.2355133367 |
|
2152873728 |
1.0025099516 |
-6965827487.98538 |
-3.2355950084 |
Table 4: Water
Again variations in roughly the 5th significant figure can be observed, and again due to the reduce tolerances used this is the order of variation we expect
The above results all support that the code is correct. While the set of tests are not as extensive as we hoped they do cover most of the important parts of the force field, especially those parts which will be affected by the promotion of the appropriate integers to 64 bits. More tests would be useful on large systems, but it has to be admitted that the process of getting 32000+ core jobs through HECToR and then debugging at that scale makes it extremely time consuming, not to say frustrating!
The code was derived from the OpenMP code described above, and is therefore also in the CCPForge repository, and will be merged with the main branch for release in the near future.
Both work packages have been successfully completed. The use of threads extends the scalability of DL_POLY_4 by up to, in a favourable case, a factor of 5-10 in the number of cores it can use, while the introduction of 64 bit integers has been demonstrated with limited simulations on systems with up to 4 billion particles. The former work package should allow marked improvements in what can be done with DL_POLY_4 from the moment of release which will occur in the very near future. The 64 bit work looks more to the future as at present only demonstration runs can be performed on HECToR, but one might expect that on ARCHER and other higher performance machines this will allow simulations on a scale that are just not possible with any other general purpose molecular dynamics package.
This project was funded under the HECToR Distributed Computational Science and Engineering (CSE) Service operated by NAG Ltd. HECToR A Research Councils UK High End Computing Service – is the UK’s national supercomputing service, managed by EPSRC on behalf of the participating Research Councils. Its mission is to support capability science and engineering in UK academia. The HECToR supercomputers are managed by UoE HPCx Ltd and the CSE Support Service is provided by NAG Ltd. http://www.hector.ac.uk.
ivI.T. Todorov, W. Smith, K. Trachenko & M.T.Dove, J. Mater. Chem., 16, 1911-1918 (2006)
v I.J. Bush, I.T. Todorov and W. Smith, Comp. Phys. Commun., 175, 323-329 (2006)
vi M.R.S. Pinches, D. Tildesley, W. Smith, 1991, Mol Simulation, 6, 51
viiVerlet, L. (1967). "Computer 'experiments' on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules". Phys. Rev. 159: 98–103.
viiiEssmann U et al. "A smooth particle mesh Ewald method" J. Chem. Phys. 103 8577 (1995)
xC. Temperton, J. Comp. Phys. 52, 1, (1983)
xiiRyckaert, J-P; Ciccotti G, Berendsen HJC (1977). "Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-Alkanes". Journal of Computational Physics 23 (3): 327–341. Bibcode:1977JCoPh..23..327R. Doi:10.1016/0021-9991(77)90098-5.
xiiiAndersen, Hans C. (1983). "RATTLE: A "Velocity" Version of the SHAKE Algorithm for Molecular Dynamics Calculations". Journal of Computational Physics 52: 24–34. Bibcode:1983JCoPh..52...24A. doi:10.1016/0021-9991(83)90014-1.
xiv"Modern Fortran Explained", Metcalf, Reid and Cohen, section 20.2.1