Quantum Monte Carlo and the CASINO program : scaling to hundreds of thousands of computer cores
M.D. Towler (University College London, University of Cambridge, Apuan Alps Centre for Physics)
D. Alfe (University College London)
W.M.C. Foulkes (Imperial College London)
S. Azadi (Imperial College London)
R.J. Needs (University of Cambridge)
L.Anton (Numerical Algorithms Group Ltd.)
Over the last couple of decades there has been an extraordinary transformation in the ability of computers to mimic the material world on the scale of individual atoms and molecules. The accuracy and realism of atomic-scale simulations have been raised to completely new heights, partly by huge increases in computer power and partly by the development of powerful techniques of various kinds. Widely-used approaches in 'computational electronic structure' include density functional theory (DFT), high-level quantum chemistry techniques such as 2nd-order Moeller-Plesset and coupled-cluster methods, computational many-body theory (for example the random-phase approximation), and the technique of chief interest to us here, namely quantum Monte Carlo (QMC). The power of supercomputers continues to grow at a dizzying rate: the petaflop barrier (1 quadrillion floating point operations per second) was broken in 2008, and exaflop speeds (1 quintillion flops) are projected for sometime around 2016. However, the materials modelling community faces a daunting challenge. The new increases in computer power are coming almost entirely from enormous increases in the number of processors, and the practical exploitation of this power will force a comprehensive reappraisal of how materials modelling is done. In the next few years, some modelling techniques will be in a better position than others. In particular, we argue that the techniques of quantum Monte Carlo are exceptionally well placed to benefit from the forthcoming technology, and we have recently been running the Cambridge QMC code 'CASINO' on some of the largest parallel machines in the world, including the UK's HECToR machine and the Jaguar supercomputer at Oak Ridge National Laboratory in the U.S.A.
The techniques that are likely to benefit most from the availability of petascale facilities are those for which the calculations can be broken into a very large number of tasks that can be executed simultaneously, preferably with only simple communications between them. Quantum Monte Carlo is a technique of this kind, because it relies on very extensive statistical sampling. Diffusion Monte Carlo (DMC) is at present the type of QMC most commonly used for high-precision calculations on materials. It works with large numbers of 'walkers', which are individual members of an ensemble of copies of the system whose job it is to explore all the various configurations of positions that the individual particles (electrons etc.) could adopt. These walkers are to quite a large extent independent of each other, and this means that groups of walkers can be given to individual processors, with only fairly light communications between them (caused by the fact that the algorithm requires individual walkers occasionally to be duplicated or deleted). DMC is thus ideally suited to large parallel machines.
We believe that there are strong scientific reasons for taking seriously the capabilities of QMC on petascale computers. Although DFT dominates atomic-scale materials modelling and will obviously continue to be extremely important, its accuracy is sometimes insufficient. When people want to comment on failures of DFT, they often like to refer to 'strongly-correlated systems', where are there are clear reasons for expecting DFT to struggle. But there are many other kinds of problems where the accuracy of DFT falls short of what is needed. An obvious example is the inclusion of van der Waals dispersion, a crucially important effect in many fields, including molecular biology, surface science and aqueous systems. Although the generalisation of DFT to include dispersion has been hugely important, there are still unsolved issues. Another important example is the adsorption energy of molecules on surfaces, where DFT is sometimes unable to give predictions of useful accuracy. DFT values of surface formation energies of quite simple paradigm materials such as silicon and magnesium oxide also depend strongly on the assumed exchange-correlation functional (the fundamental underlying approximation in DFT) and there is usually no way of knowing in advance which functional to trust. The well-known problem of calculating electronic band gaps could also be mentioned.
The urgent practical need to do better in these and other areas is driving current efforts to develop more accurate methods, and the phrase 'beyond DFT' has become familiar over the past few years. The introduction of hybrid exchange-correlation functionals combining ideas from DFT and Hartree-Fock theory has improved the accuracy attainable in some regimes, and combinations of DFT with ideas from many-body theory have produced new techniques such as DFT + Dynamical Mean-Field Theory and DFT + Gutzwiller, which show promise in strongly-correlated systems.
There is abundant evidence that there are large classes of problems for which QMC techniques are considerably more accurate than conventional DFT. One of the main factors that has tended to deter researchers from applying QMC to their problems is that it demands much larger computer resources than DFT. Roughly speaking, one can expect a DMC calculation of the ground-state energy of a reasonably-sized assembly of atoms in a given geometry to take about 10000 times more CPU time than the same calculation with standard (as opposed to hybrid) DFT. Obviously, 10000 is a large factor, but it happens to be very similar to the factor by which supercomputer power grew from 1993 to 2008. This means that the situation with QMC now is similar to the DFT situation in the early 1990s, which was when the parallelisation of DFT first started to make an impact on materials modelling. The kinds of DFT calculations that appeared ridiculously daunting then are now performed routinely on desktop machines, and will presumably be performed by smart-phone apps in the future. A similar evolution path may well be followed by QMC, and we believe that now is the time to find out what can be achieved with QMC on petascale machines.
In order to achieve this goal, we first needed to verify how CASINO scales on large numbers of processors, and if necessary to improve it. Ideally, we would like to have 'perfect parallel scaling', that is, we double the number of processors and in consequence halve the required wall-clock time, but this is notoriously difficult to achieve. Parallel scaling is a particularly serious problem for DFT and 'DFT +' methods. Some scale better than others, but all require too much communication between processors and become less efficient as the number of processors increases. Eventually, the wall-clock time no longer decreases at all as the number of processors rises. At present, it looks unlikely that DFT will be able to make efficient use of machines with hundreds of thousands of processors, except by using them to run hundreds of separate small simulations simultaneously. QMC methods scale much better.
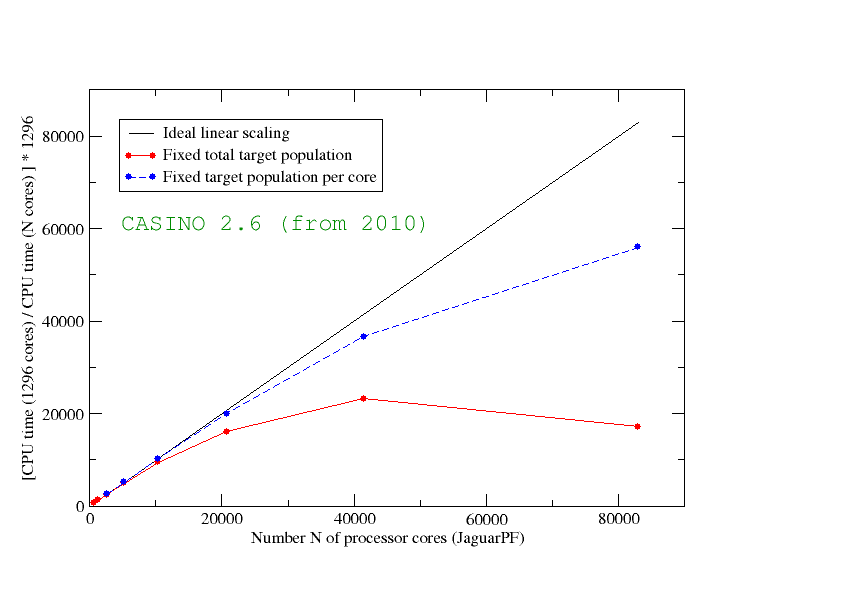
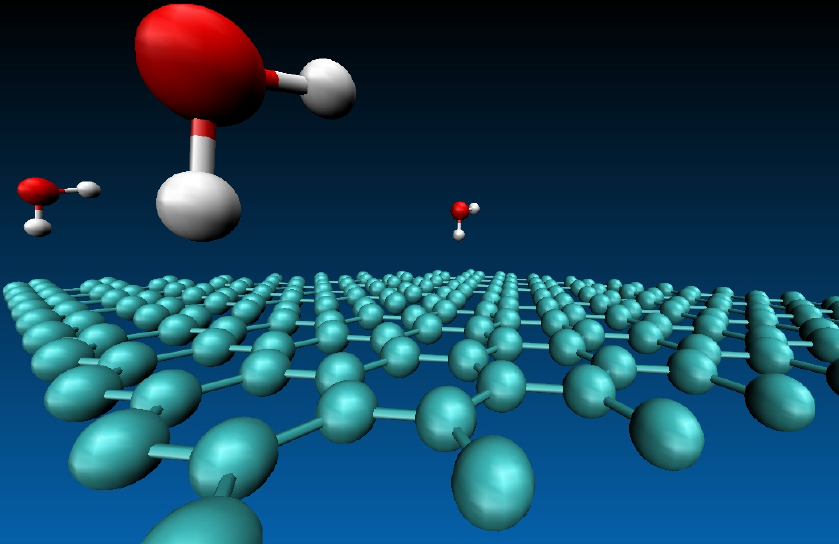
For a typical largish calculation, we found that an earlier version of CASINO (2.6) scaled as in the diagram above. Although the code scales well for a few tens of thousands of processing cores, the performance falls off as we approach 100000 cores and perfect parallel scaling was clearly far from being achieved in practice. The plot shows the scaled ratio of CPU times using different numbers of cores for a calculation of one water molecule adsorbed on a two-dimensionally-periodic sheet of graphene containing fifty carbon atoms per unit cell, as illustrated in the figure below. 'Ideal scaling' is represented by the solid black line, and the blue and red lines show the actual performance of CASINO. Both blue and red lines show results for fixed sample size, which we define as the target number of walkers times the number of moves (the behaviour for a fixed problem size is normally referred to as 'strong scaling'). However, the blue line used a fixed target population of 100 walkers per core (with an appropriately varying number of moves). The red line comes from a fixed target population of 486000 (and a constant number of moves), i.e., the number of walkers per core falls with increasing number of cores (from 750 to around 5). The fact that the performance indicated by the red line falls off much more quickly with increasing numbers of processor cores shows the importance of making sure that each core has 'enough to do'.
The deviation from ideal linear scaling occurs largely because of the need to 'load balance' the populations of walkers on each core, that is, to ensure that each core has approximately the same number of walkers to deal with. This requires the frequent 'sending' of walkers from one core to another. Following a study by the head of the CASINO development team, Mike Towler, it was realized that with a few tricks one can effectively eliminate all overhead due to walker transfers, and hence hugely improve the scaling, as shown in the following plot:
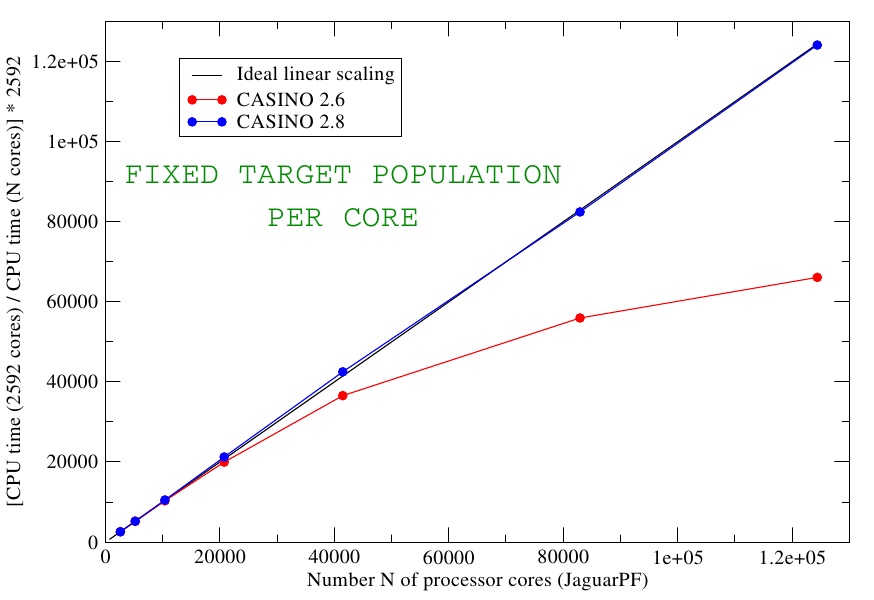
It is evident that, compared to the old code, the new CASINO 2.8 code (which became CASINO 2.10 in Feb 2012) shows essentially perfect parallel scaling out to 124000 cores and beyond.
The new algorithm involved:
- (1) Analysis and modification of the procedure for deciding which walkers to send between which pairs of cores when doing the load balancing (the original CASINO algorithm for this originally scaled linearly with the number of cores -- when you need it to be constant -- yet this was never really taken account of in formal analyses).
- (2) The use of 'asynchronous, non-blocking' MPI communications.
To send a message from one processor to another, one normally calls 'blocking' MPI_SEND and MPI_RECV routines - which are part of an internal 'Message Passing Interface' (MPI) library supplied on parallel machines - on a pair of communicating cores. 'Blocking' means that all other work will halt until the transfer completes. However, one may also use 'non-blocking' MPI calls, which in principle allow cores to continue doing computations while communication with another core is still pending. On calling the non-blocking MPI_ISEND routine, for example, the function will return immediately, usually before the data has finished being sent. Considerable care has to be taken for the code not to get confused when doing this, but CASINO now seems to manage this very well.
A set of slides for a talk given by Mike Towler on this topic which give some of the technical details of how all this was achieved are available here.
It is clear, then, that the availability of petascale computers having tens or hundreds of thousands of cores is opening up completely new possibilities for the techniques of quantum Monte Carlo. The capabilities of the UK HECToR machine have been fundamental in allowing us to demonstrate this. These developments are scientifically important, as we have already stated, since for important types of problems QMC gives much greater accuracy than standard DFT methods, and some of the well known deficiencies of DFT can thus simply be overcome. In a huge range of system types there is a pressing need for accurate benchmarks which can be used to test and calibrate DFT approximations, and it is increasingly clear that QMC can deliver these benchmarks in practice.
Until fairly recently, QMC has sometimes been regarded as a bit of a minority interest, principally because of the very large computational demands. However, we believe that the arrival of petascale computing, and the prospect of exascale computing in the next five to ten years will change all this. One has to remember that when DFT first began to be used for molecular dynamics problems over twenty-five years ago, it was sometimes commented that the computational requirements of DFT were completely prohibitive and that the technique would never be widely used for practical problems. Obviously, the critics have been proved wrong. Given that available computing power has increased by at least a factor of 10000 over the past fifteen years, and that QMC is ideally suited to massively parallel architectures, it takes little imagination to see that QMC may follow the same kind of evolution. The rise of GPU accelerator technology is obviously extremely important to the future of supercomputing, and CASINO is being further improved in collaboration with NAG Ltd. to take advantage of this. Given the developments that are underway, we believe it is now very timely for more research groups to consider becoming involved in the QMC enterprise.
This work was supported by EPSRC Software Development Grant EP/I030190/1, "Quantum Monte Carlo simulations on ten thousand to a million cores".