Benchmarking and scalability of the coupled algorithm

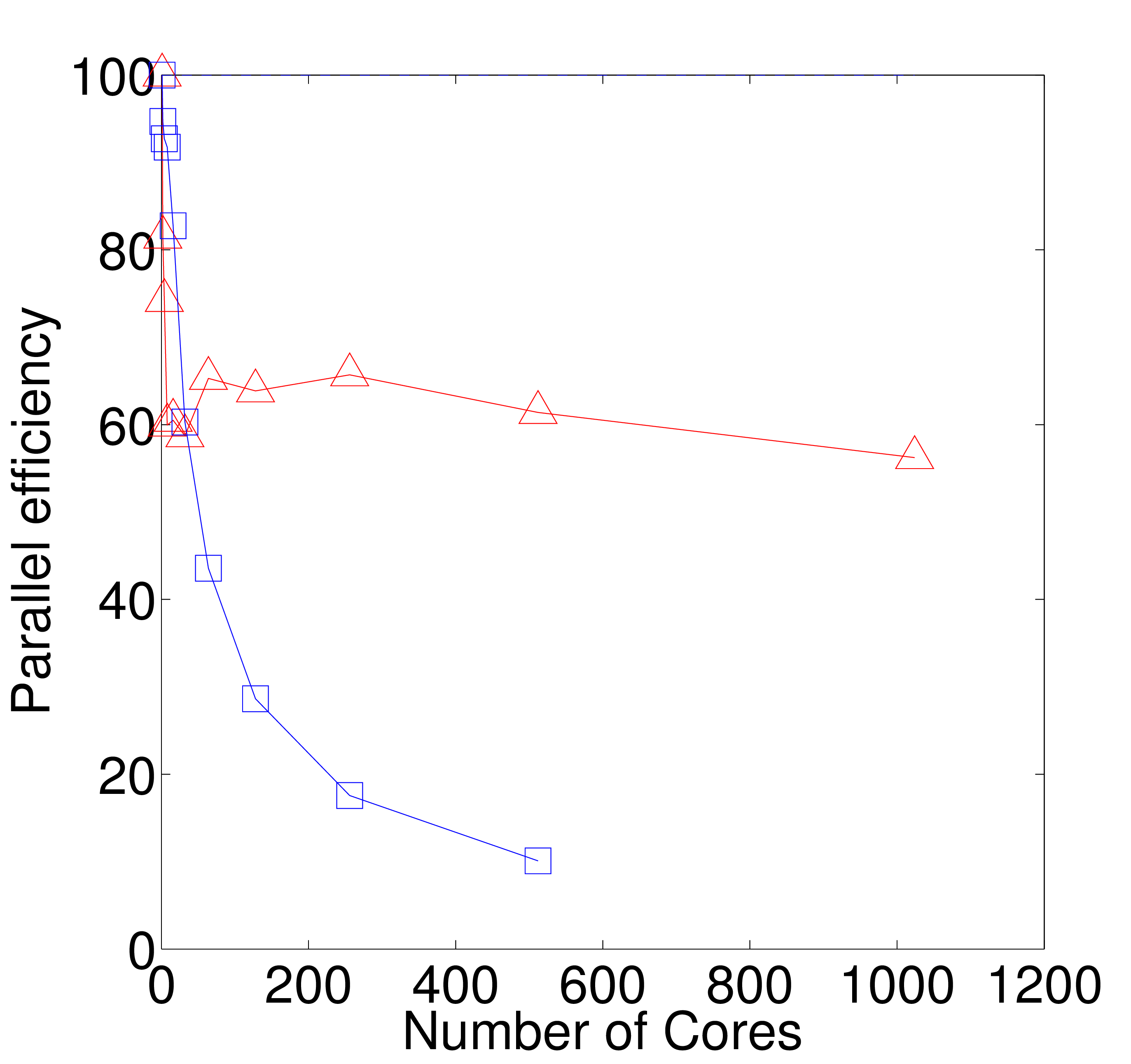
Before benchmarking the coupled algorithms, the scaling of the individual codes is presented in figure 2. An efficient coupler should ensure the scaling of the individual codes is maintained

Performance testing for $\mathcal{T}rans$ $\mathcal{F}low$ was carried out using a curvilinear mesh, for turbulent flow around a compressor blade. The flow was simulated using 370,000 grid points per MPI-task, on an SGI Altix 4700, Intel Itanium 2 (HLRB, Super-Computing Centre, Germany). Parallel efficiency is defined with respect to the performance on 16 cores. As the number of cores is increased, the number of nodes per core is held fixed. At 768 cores, the algorithm performed at 94.4% parallel efficiency, shown in figure 2a.

As part of the development under work package one, $\mathcal{S}tream$$MD$ has been benchmarked using 1024 cores on HECToR. The profile shown in figure 2b is for 5000 iterations of a Lennard Jones system with 3,317,760 molecules. The number of processors is increased for this system size and the parallel efficiency is defined as the simulation time relative to the ideal scaling of a single core. The results compare favourably with those obtained from profiling of LAMMPS. The higher efficiency of $\mathcal{S}tream$$MD$ is in part due to the numerical method, but it should also be noted that LAMMPS was tested with a smaller system size (32,000 molecules) and hence efficiency is quickly reduced at larger numbers of cores.

Figure 2: (a) Parallel performance of TransFlow.

Figure 2: (b) Parallel performance StreamMD vs. LAMMPS on a Cray X5. Parallel performance of the two codes profiled individually.

                

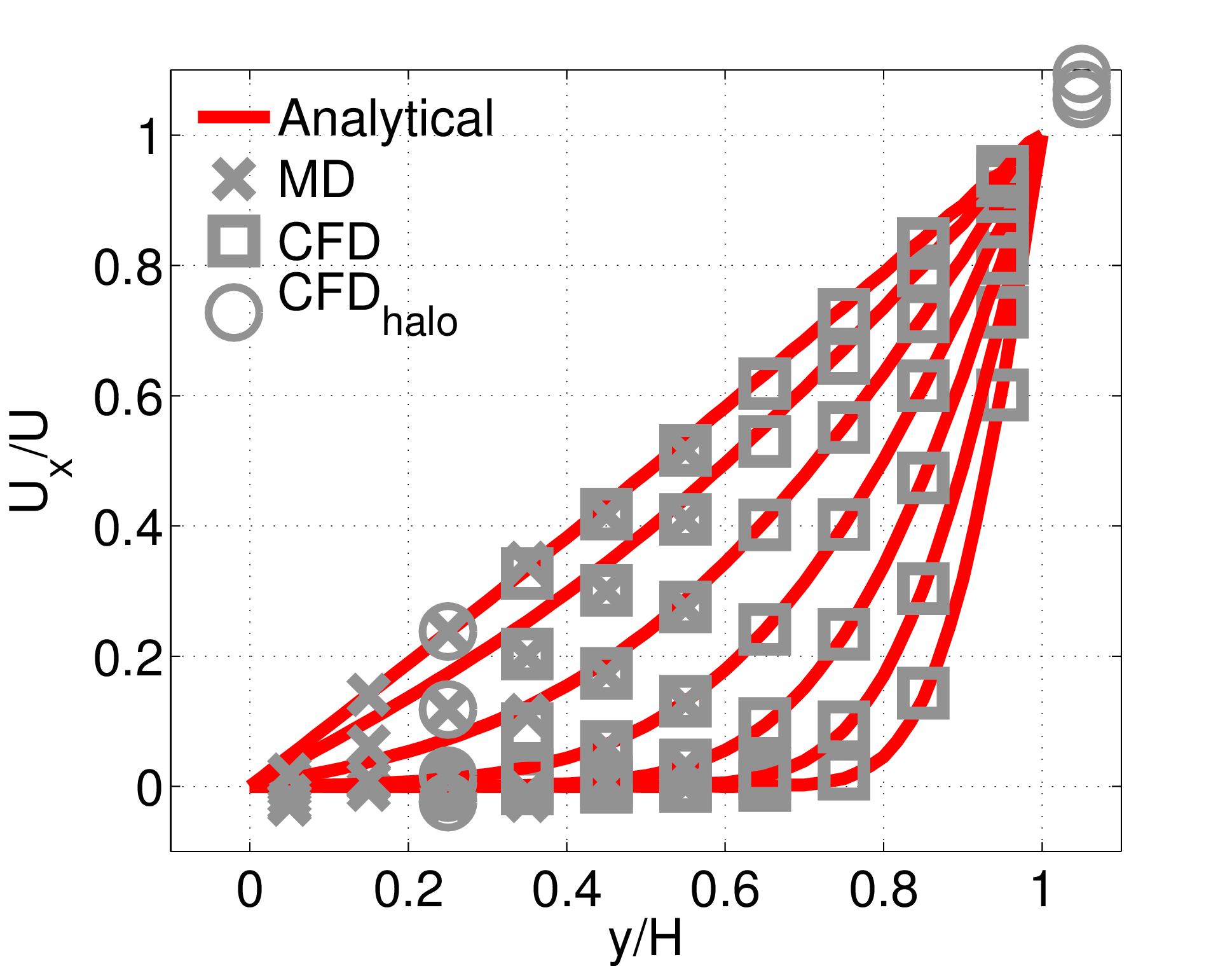
The coupling methodology follows the work of [3] and the accuracy of the coupled algorithm has been verified by recreating results from that paper. The simulated problem is the canonical sheared Couette flow, and therefore it is possible to compare the numerical result to an analytical solution. Figure 3a shows the recreation of the results presented in [3] along with the analytical results. The coupled continuum-MD code accurately reproduces the analytical solution.

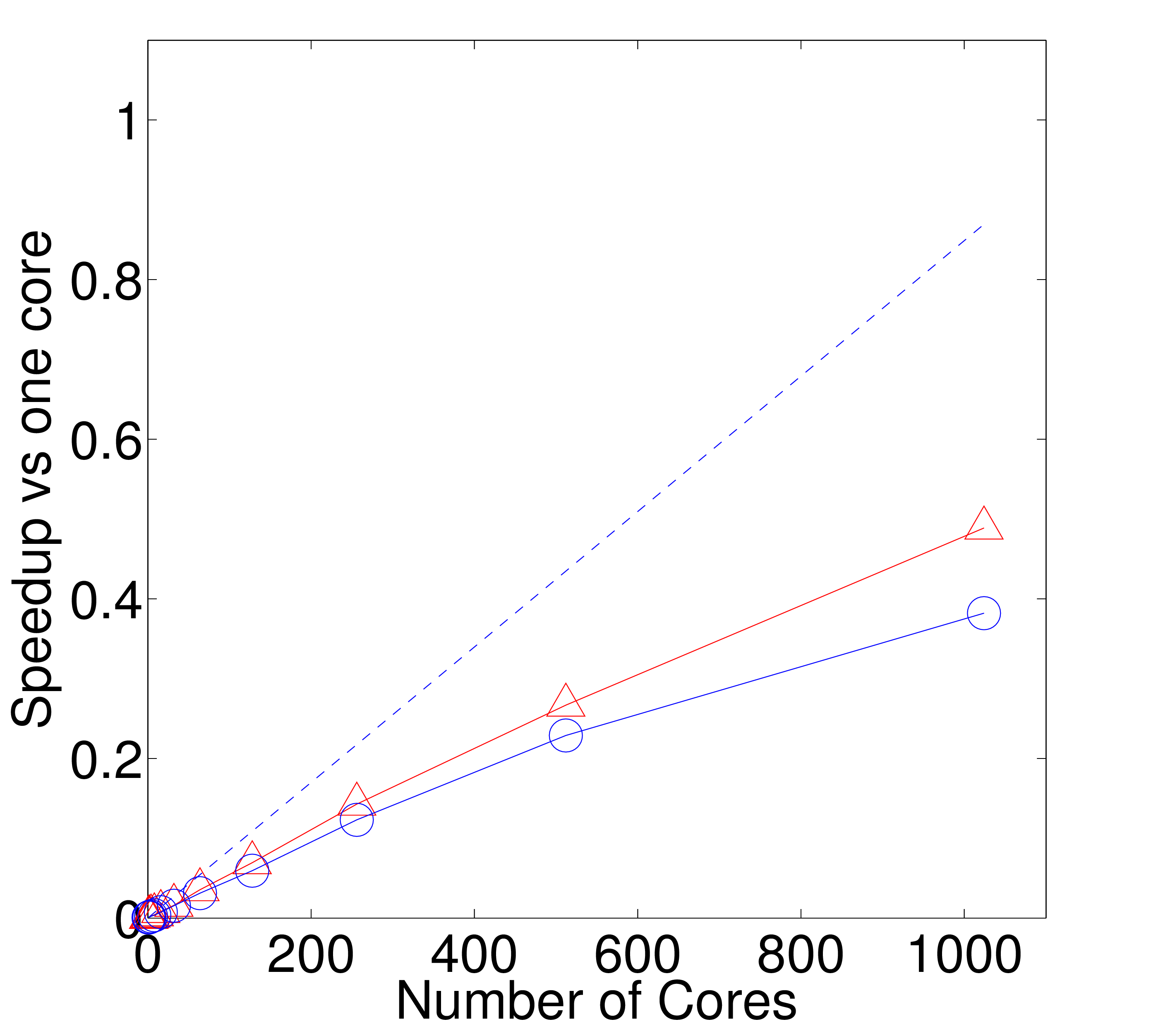
Scalability of the coupled algorithm was also evaluated. For the case of laminar Couette flow, the computational requirements of the continuum solver are almost negligible. The speedup of the code therefore depends almost entirely on the scaling of $\mathcal{S}tream$$MD$ and the coupler. If the coupler is performing efficiently, this combined speedup can be expected to be similar to the scaling of $\mathcal{S}tream$$MD$ alone. The scaling of the coupler is compared to $\mathcal{S}tream$$MD$ in figure 3b, up to 1024 processes. Figure 3b demonstrates that the coupler performance only slightly deteriorates speedup.

Figure 3: (a) Verification of the coupled codes against analytical solution for Couette flow. Accuracy of the coupled application.

Figure 3: (b) Parallel speedup of StreamMD only and coupled code against the ideal speadup. Scalability of the coupled application.