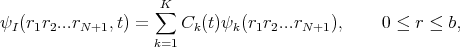
Abstract
The RMT method (R-Matrix with time-dependence) is a new ab initio method for solving the
time-dependent Schrödinger Equation (TDSE) for multi-electron atomic and molecular systems
in intense short laser pulses. Although several other time-dependent R-Matrix methods have
been introduced in recent years [1, 2, 3, 4, 5, 6], RMT demonstrates orders-of-magnitude
improvements in efficiency, primarily because it employs finite-difference (FD) techniques to model the
few-electron wavefunction far from the atomic core. RMT merges the Outer Region FD model
with a classic B-Spline R-Matrix basis set for the multi-electron Inner Region [7]. The difficult
problem of merging a basis set model with a spatially adjacent FD model, while maintaining
the unitarity of the time-propagator, has been a long-standing barrier to progress in this field.
RMT is based on the solution first published in 2008 by Nikolopoulos, Parker and Taylor [8].
In this report we discuss the implementation and testing of a new RMT code for calculating the spectrum of
light scattered by atoms interacting with intense-field laser pulses. At sufficiently high laser
intensities, atoms scatter the incident radiation not just at the frequency of the laser, but also at
odd-integer multiples of the laser frequency. This process we refer to as High Harmonic Generation
(HHG). The spectrum of light scattered in HHG processes is obtained directly from the Fourier
transform of the time-dependent expectation value of the acceleration induced by the external light
source (the laser pulse). The bulk of this project has been devoted writing new code to calculate
these expectation values, and to the much more difficult problem of assessing its correctness.
High harmonic spectra provide rich information about the electronic structure of atoms and molecules, in
some cases with unprecedented time and spatial resolution. Experimental research groups at Imperial College
London, University College London and CLF have used the information contained in the high-harmonic
spectra to probe the electronic structure of polyatomic molecules [13]. The group at Imperial College has also
recently pioneered the PACER technique [14] to study dynamical nuclear interference effects in molecules on
an attosecond time scale [15].
Of the various theoretical approaches to the study of high harmonic generation, RMT is particularly well
suited because it naturally models multiple final states of the residual ion created during ionisation, each of
which needs to be accurately accounted for throughout the calculation. No other computer code to our
knowledge, except HELIUM, can generate these time-dependent solutions to high accuracy. Moreover, recent
attempts at developing models that go beyond the single-active-electron approximation are strongly
suggestive of a crucial role played by multi-electron dynamics in determining the HHG emission rates in
multi-electron atoms [16], but such models are still unable to provide a quantitative description of HHG
yields. The need for an accurate quantitative description of HHG from rare gas atoms in order to provide
guidance for future experimental investigations is the motivating factor behind our objective to
implement the coding to make possible the calculation of high harmonic processes in the RMT code.
Although high harmonic generation specifically in molecules is of particular interest to UK experimentalists
at Imperial College London and elsewhere and a RMT description of this process in multi-electron molecules
is an eventual goal, it is first necessary to implement coding to make RMT calculation of this process possible
for multi-electron atoms. This is because the HELIUM code provides a suitable code comparator role for
the atomic case, helping the correctness of the new coding to be established. In a later stage
(outside the scope of the current project) the RMT atomic code will play a similar comparator code
role when implementing coding for the high harmonic generation process in a RMT molecular
code.
Over the last 5 years, remarkable advances in laser technology have enabled experimental study of
matter-laser interactions with unprecedented time-resolution. Experiments can now be performed using
few-cycle pulses of high-intensity Ti:Sapphire laser light at 800 nm wavelengths, and at Vacuum-Ultraviolet
wavelengths (VUV) with pulses as short as 250 attoseconds. The creation of attosecond pulses in particular
has opened up a new frontier in the study of ultra-fast electronic processes. Recent landmark attosecond
spectroscopic measurements in a solid [9] have demonstrated that ultra-fast techniques can probe solid state
processes occurring at the theoretical ultimate speed limit for electronics. Attosecond pulses have recently
enabled the real-time observation of electron tunnelling in atoms [10] and Auger decay of inner-shell
electrons [11]. Attosecond pulses have also enabled stroboscopic study of single ionisation events in argon
[12].
The goal of RMT has been to enable theoretical analysis of recent experimental advances with a degree of
reliability that would be impossible by competing methods. These include time-resolved studies of
ionisation events in attosecond time-scales, studies of time-delays between the ejection of electrons in
double-ionisation, inner shell excitations and decays in complex atoms, intense-field atom-laser interactions
in the XUV limit using the new free-electron x-ray lasers, and harmonic generation in atoms and molecules.
In a previous distributed CSE project we demonstrated that the RMT method is both computationally stable
and could be distributed over 1000’s of cores with good efficiency. Success was due to the use of a mature
R-Matrix parallel code for the Inner Region, and the use of the HELIUM finite-difference code for the Outer
Region [17, 18]. In this project, a significant fraction of the effort has been devoted to assessing RMT by
comparing the results of large-scale RMT integrations of laser-driven helium with the results of identical
numerical integrations using the HELIUM code. HELIUM [19, 20] is a finite-difference code designed to
generate high-integrity solutions of the full-dimensional time-dependent Schrödinger equation (TDSE)
for two-electron atoms or ions in intense fields. HELIUM has been in heavy use on massively
parallel machines since the arrival of the original Cray T3D over 15 years ago. The two methods of
integrating the TDSE, the R-Matrix based RMT and the finite-difference based HELIUM, could
not be more different. As we will demonstrate here, the two methods give good agreement in a
series of rigorous tests that exercise mainly the inner (R-Matrix) region of the RMT code. The
tests focus on harmonic generation by a helium atom irradiated by extremely short (attosecond)
intense-field UV laser pulse and optical laser pulses. The good agreement observed between the two
algorithmic methods helps to confirm that the methods and implementations are basically sound.
In section 2 we discuss the goals and outcomes of Work Package 1, and we present the results
of a significant test of the new code (as outlined in Work Package 3). The objective of Work
Package 1 was to develop and test new RMT code for the calculation High Harmonic Generation
(HHG) - the light scattered and shifted to higher frequencies by atoms interacting with intense
laser radiation. The relevant Work Package 3 test is a comparison of two RMT calculations of
HHG, the first derived from acceleration expectation values and the second derived from dipole
expectation values. The two approaches are found to give good qualitative agreement over a 9 orders
of magnitude range. Additionally we present measurements of the new RMT code’s scaling
properties on HECToR, using a small 1-state helium-atom RMT calculation on a range of 34
to 1120 HECToR cores. We note that RMT calculations in more complicated atoms like neon
would likely require an order of magnitude larger core count for both the inner and outer regions.
In section 3 we discuss the goals and outcomes of Work Package 2, and we present the results of one of the
tests of the new code (as outlined in Work Package 3). The objective of Work Package 2 was to perform the
same set of enhancements to the HELIUM code that were developed for the RMT code as described in
section 2. The relevant Work Package 3 test is the same as the one described in section 2 for
the new RMT code, a comparison of the high harmonic spectrum derived from acceleration
expectation values with that derived from dipole expectation values. In HELIUM there is only one
region, so no additional MPI communication software was required, but the integration is over
two electrons (6 dimensional) instead of one, requiring a more laborious calculation of dipole
expectation values < ψ(r1,r2,t)|z1 + z2|ψ(r1,r2,t) > , and acceleration expectation values
< ψ(r1,r2,t)|dp1∕dt + dp2∕dt|ψ(r1,r2,t) >. We demonstrate that HELIUM HHG calculations based on
acceleration expectation values and on the dipole expectation values give good qualitative agreement over an
11 orders of magnitude range.
In section 4 we discuss the goals and outcomes of Work Package 3. The objective of Work Package 3 was to
test and tune the new code developments for numerical correctness and accuracy. Two of the more rigorous
tests were discussed in sections 2 and 3. These two tests verified that the dipole expectation values and
acceleration expectation values yield agreement in HHG calculations. In section 4 we continue with a
series of tests that compare the predictions of RMT with those of HELIUM over a range of laser
frequencies. We report good agreement between the two methods, which improves confidence in the
correctness of the RMT code, and demonstrates that the RMT integration parameters have been
properly tuned to produce numerical integrations comparable in quality to those of HELIUM.
We begin with an outline of the basic RMT equations. The RMT wavefunction is the sum of an Outer and an
Inner Region wavefunction. The Outer Region wavefunction is written on a finite-difference grid, and
represents the single electron ejected from the atom by the laser pulse. The Inner Region wavefunction is
described by a B-spline basis set. The Inner Region uses R-Matrix methods to treat the quantum mechanical
dynamics of the multi-electron atom within a spherical shell of some fixed radius. In the following, that
radius will always be 20 atomic units.
We write in the Inner Region I where all electrons can be found:
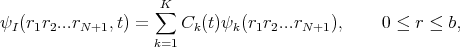 | (1) |
where ψk(r1r2...rN+1),k = 1,K form a field-free, time-independent R-Matrix basis for the (N + 1)
electrons within the Inner Region with outer boundary at r = b. The construction of the ψk is the
responsibility of long-existing atomic R-Matrix time-independent codes. The time evolution of the Inner
Region time-dependent wavefunction is entirely contained in the coefficients Ck(t) whose time
evolution is determined by the TDSE. However in writing the TDSE we must take care that
the Hamiltonian and dipole operators which act on ψI(r1r2...rN+1,t) are Hermitian over Inner
Region I (where ψI(r,t) is only defined). The Hermitian Inner Region Hamiltonian is given by
HI = H0 +  h and the dipole operator by DI = D +
h and the dipole operator by DI = D +  d, where
d, where 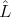 h and
h and 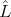 d are Bloch surface
terms, only non-zero at r = b. In these circumstances the TDSE over Inner Region I is written:
d are Bloch surface
terms, only non-zero at r = b. In these circumstances the TDSE over Inner Region I is written:
![dψ [ ]
i--I(r1r2...rN+1,t) = [HI + DI (t)]ψI(r1r2...rN+1,t) - ˆLh + ˆLd(t) ψ (r,t),
dt](dcse_hhg_report_20125x.png) | (2) |
where 0 ≤ r ≤ b.
This equation is a key one to the method. The second term on the right hand side compensates for the Bloch
terms introduced to make HI and DI Hermitian. Note that it makes a contribution only at r = b and brings
into play there ψ(r,t) a one-electron wavefunction form which we define from just within the Inner Region
outwards. This term is central to any time propagation scheme in Inner Region I because it connects
the wavefunction form ψI(r1r2...rN+1,t) specific to that region with a wavefunction form that
at r = b represents a single electron and which in calculations is obtained from Outer Region
II.
The Outer Region II is spanned by a finite-difference (FD) grid so that the one-electron wavefunction there is written
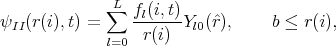 | (3) |
with i = ib,..,I and r(ib) = b. In this form, for simplicity of presentation, we have allowed for only one residual ion state of the system. The form the TDSE takes in this Outer Region is then
![f˙l(i,t) = - i[H ⋅ F ]l(i,t) + δiib [B0l(ib - 1,t) + B0l(ib - 2,t)] + δiib+1B1l(ib - 1, t).](dcse_hhg_report_20127x.png) | (4) |
This, the second key equation to the method, is the normal form of the TDSE over a FD grid except for the
terms multiplying δiib and δiib+1. Note that these terms require quantities (the Bs) to be evaluated at grid
points ib - 1 and ib - 2 i.e. at points on the inner side of the boundary at r = b. This assume we are using
5-point difference operators on the FD grid.
We emphasize how Eqs. (2) and (4) are actually used by sketching the computational procedure in
propagating the full wavefunction through one time-step from t to t + τ. We first consider the Outer Region
TDSE, Eq. (4). This is handled by the explicit Arnoldi time-propagator method [19] as in HELIUM and
brings into play Inner Region information through the B0l(ib - 1,t), B0l(ib - 2,t) and B1l(ib - 1,t) terms all
known from time t. Having thus determined all the fl(i,t + τ) for i = ib,..,I we proceed to the Inner
Region. What we need to determine here are the coefficients Ck(t + τ) and again these are determined
by the explicit Arnoldi time-propagator using knowledge of the Outer Region fl(i,t + τ) to
determine the spatial derivative terms at r = b brought in by the non-zero Bloch operator terms
there.
Attempts to create efficient time-dependent R-Matrix integrations for such large volumes have made slow
progress, largely because successful integration of the relevant high-dimensional partial differential equations
is so computationally demanding that it requires the benefit of parallelization over tens of thousands of cores,
which is not straightforward in pure R-Matrix formalisms.
We turn now to a discussion of the scaling properties of the new RMT high harmonic generation code on
HECToR. The performance and scaling of RMT is somewhat degraded by the additional computational
overhead of the calculation of acceleration and the global MPI communications operations needed to
complete, assemble and print the calculation of expectation values. To demonstrate the behaviour of
the new RMT code, we choose parameters expected to be appropriate to harmonic generation
problems in study of laser-molecule interactions. In these problems, the laser wavelengths are
typically infra-red, and long in duration in order to resolve resonances with high accuracy. The
numerical integrations in these cases require large integration volumes in order to accommodate
the ionising electron during the duration of the laser pulse. By contrast, in a typical HELIUM
integration at high (UV) frequency a small integration volume of 1000 a.u. might be used. In
the present problem, figure 1, a volume of radius 3200 is used. The example shown in figure 1
uses a helium atom with a single target state for each possible final state angular momentum.
The inner region Hamiltonian is a tri-diagonal block matrix, of size 32 x 32 blocks. Each block
is a 55 x 55 matrix. A more complicated atom, like neon, or a configuration with more target
states would likely require an inner region Hamiltonian one of more orders of magnitude larger.
The minimum number of cores needed to accommodate the inner region is 32. Using more than 64 cores
provides no additional improvement in speed because of the small size of the blocks (55 x 55). Figure 1
demonstrates this. The measurements, up to 1056 cores, are made maintaining the inner region core-count at
a constant 32 cores, the minimum workable number. All of the other cores are applied to the outer region.
After the 1056 core limit is reached, very little benefit is obtained by applying more cores to the outer region
calculation.
As a final step, we increase the inner region core count from 32 to 64. A sharp jump in speed is produced by
the addition of these 32 inner region cores, and the result is plotted at the end of the data curve in figure 1.
A 50% improvement in integration speed is observed, (from 200 steps/sec to 300 steps/sec).
In the following paragraphs we introduce some of the basic equations describing harmonic generation by
atoms in intense laser radiation. Most of the tests described in this report will involve calculation of high
harmonic energy spectra, or of expectation values useful in the calculation of energy spectra. The tests will
generally exercise both HELIUM and RMT, and in the last section the results of the HELIUM and RMT
calculations will be compared. The problem of testing, estimating uncertainties, and detecting error is
often the most difficult part of a numerical integration, especially on large parallel machines
which are unusually prone to system failures. The opportunity to provide independently generated
solutions for comparison with the RMT results is therefore fortunate. HELIUM, for example,
was originally developed in conjunction with the time-independent R-Matrix Floquet method.
Discrepencies between the predictions helped revealed the limits in which the numerical methods became
unreliable (as for the example the high intensity limit). When agreement is observed, the small
remaining differences can be used to infer a lower bound on the uncertainties in the numerical result.
The electric field, E, of light scattered by an atom in linearly polarized radiation is proportional to the acceleration induced by the laser, which we choose to be polarized in the z-direction. Using the Lienard-Wiechert potential (in the non-relativistic far-field limit), the electric field radiated by an accelerated charge is
![⟨ | | ⟩ ⟨ | | ⟩
-d || e- || ||[pz,H-]||
E = kdt ψ (t) |pz - c Alaser(t)|ψ(t) = k ψ (t)|| i¯h ||ψ (t) + keElaser(t)](dcse_hhg_report_20129x.png) | (5) |
where H is the Hamiltonian describing the laser-atom interaction, Pz = pz - Alaser(t) is the mechanical
momentum of the charge, pz is the canonical momentum, and k is a proportionality constant. The energy
spectrum of the scattered radiation is given by the square modulus of the Fourier transform of Etotal(t),
where Etotal(t) is the coherent sum of the E-fields radiated by the N + 1 electrons. In practice, we need to
calculate expectation values of
Alaser(t) is the mechanical
momentum of the charge, pz is the canonical momentum, and k is a proportionality constant. The energy
spectrum of the scattered radiation is given by the square modulus of the Fourier transform of Etotal(t),
where Etotal(t) is the coherent sum of the E-fields radiated by the N + 1 electrons. In practice, we need to
calculate expectation values of ![[pz,H ]](dcse_hhg_report_201211x.png) = -iℏ∑
j(d∕dzj)V (r1,...,rN+1), where V is the sum of the (N + 1)
electron-nucleus Coulomb potentials. The electron-electron potentials, 1∕rij, do not contribute to the above
quantity.
= -iℏ∑
j(d∕dzj)V (r1,...,rN+1), where V is the sum of the (N + 1)
electron-nucleus Coulomb potentials. The electron-electron potentials, 1∕rij, do not contribute to the above
quantity.
The calculation of the expectation value ⟨ψ(t)|![[pz,H]
i¯h](dcse_hhg_report_201212x.png) |ψ(t)⟩ involves an integration over the spatial variables of
all (N + 1) electrons described by ψ(t). The integration is performed over all angular variables and over all
radial variables, and therefore contributions will arise from both the Inner Region (r1,...,rN+1 ≤ b) and from
the Outer Region (r1,...,rN ≤ b and rN+1 > b). The wavefunction forms in the Inner and Outer Regions are
given by Eqs. (1) and (3) respectively.
|ψ(t)⟩ involves an integration over the spatial variables of
all (N + 1) electrons described by ψ(t). The integration is performed over all angular variables and over all
radial variables, and therefore contributions will arise from both the Inner Region (r1,...,rN+1 ≤ b) and from
the Outer Region (r1,...,rN ≤ b and rN+1 > b). The wavefunction forms in the Inner and Outer Regions are
given by Eqs. (1) and (3) respectively.
A common practice in calculations of the spectrum of scattered light is to use z(ω) (the Fourier
transform of ⟨ψ(t)|z|ψ(t)⟩) because a simple relation exists between z(ω) and acceleration az(ω),
the latter defined as the Fourier transform of (d2∕dt2)⟨ψ(t)|z|ψ(t)⟩, which we calculate using
iℏd∕dt⟨ψ(t)|pz|ψ(t)⟩ = ⟨ψ(t)|[pz,H]|ψ(t)⟩. In the case in which these time-dependent functions and their
derivatives start at zero and decay to zero at the end of the integration (a condition that is usually enforced
artificially by applying a windowing function like the Hanning window) we have az(ω) = -ω2z(ω). Of
course this is a mathematical result that is maintained by the integration only in the absence of numerical
approximation, an ideal and unattainable limit.
Integration error can be catastrophic in high harmonic calculations because the part of (d2∕dt2)⟨ψ(t)|z|ψ(t)⟩
that is of interest, (the signal that gives rise to the high harmonics of the laser frequency), is often many
orders of magnitude smaller than the signal giving rise to scattered light at the frequency of the
driving laser. For example, errors of 1 part in 105 in the wavefunction ψ can easily obliterate the
information containing the high harmonics. In that case we would see numerical noise instead of high
harmonics.
The calculation of z(ω) in conjunction with az(ω) therefore has an additional benefit, the value of which
cannot be overstated. Comparison of these two quantities provides us with a natural test of the quality of the
numerical integration. As remarked above, perfect numerics would yield az(ω) = -ω2z(ω). In practice, the
degree to which this equality is satisfied is sensitive to convergence of ψ on the B-spline basis set, the
matching of the Inner Region and Outer Region wavefunctions at the boundary, the reflection of
wavefunction at boundaries of the integration volume, and accumulation of roundoff error during
propagation.
|
|
|
|
In Fig. 2 we show the results of an RMT calculation of the energy spectrum of scattered light. The
energy spectrum is proportional to |Ez(ω)|2, where ω is the frequency of the scattered light, and
Ez(ω) is the Fourier transform of the time-evolving electric field of the scattered light in the z
direction, Ez(t). The energy spectrum gives the total energy scattered in a frequency range. By
Parceval’s Theorem, the integration over all frequencies ω of |Ez(ω)|2 equals the integration
over all time of |Ez(t)|2. The latter quantity is proportional to the intensity of scattered light as
measured by a detector in the far field, (a great distance from the atom). Intensity of light has the
units: joules per second per square meter. Integration of intensity over all time (really over the
length of the pulse) would yield the total energy (joules) contained in the z component of the
electric field, as measured by a perfect detector (per square meter of the detector). Similarly,
integration over a frequency range of |Ez(ω)|2 would yield, up to proportionality constant, the energy
measured by a frequency sensitive detector in that frequency range. The absolute values of the
intensity and of the energy spectrum depend on the systems of units, and the geometry and position
of the detector, which are not of interest in the software testing. Units are therefore arbitrary.
Figure 2 compares the energy spectrum as calculated by acceleration expectation values (Eq. 5) with
the spectrum obtained by dipole expectation values. The expectation values are obtained by
using only the RMT inner region (B-Spline) wavefunction. For comparison, Fig. 3 shows the
calculation repeated with the outer region (finite-difference) RMT wavefunction added in. The use of
the full wavefunction in Fig. 3 results in a small but detectable improvement in the agreement
between the two methods of calculating the spectrum. The dipole method now agrees well with
the acceleration calculation at the 3rd peak (5th harmonic), and gives a background (the high
frequency limit of the spectrum) which is smaller than the corresponding background in Fig. 2.
In this section we test the upgraded HELIUM code on a similar case as that used to test the new RMT code in
the previous section, namely a comparison of the high harmonic spectrum derived from acceleration
expectation values with that derived from dipole expectation values. Again, the TDSE for helium in a short
high frequency (0.457 au) laser pulse is numerically integrated and the dipole and acceleration expectation
values are tabulated over the duration of the pulse. In HELIUM there is only one region, so no additional MPI
communication software was required, but the integration is over two electrons (6 dimensional) instead of
one. The dipole expectation values are < ψ(r1,r2,t)|z1 + z2|ψ(r1,r2,t) > , and the acceleration expectation
values < ψ(r1,r2,t)|dp1∕dt + dp2∕dt|ψ(r1,r2,t) >.
Figure 4 shows the results of a HELIUM calculation the energy spectrum of scattered light. The energy
spectrum is proportional to |Ez(ω)|2, the Fourier transform (modulus squared) of the electric field of the
scattered light, Ez(t). The meanings of these quantities are discussed in more detail in the previous
section. Again we find that if dipole expectation values are used to calculate the energy spectrum
then the high frequency part of the spectrum is less accurate than the acceleration calculation.
|
|
In this section we present a series of comparisons between the predictions of RMT and those of HELIUM
over a range of UV laser frequencies (0.1168 au to 0.94 au). Good agreement is observed between the two
methods, confirming that the RMT integration parameters have been properly tuned to produce numerical
integrations comparable in quality to those of HELIUM. The success of these tests does much
to increase confidence in the correctness of the two highly dissimilar numerical integrations.
Figure 5 shows the results of the two numerical integrations at the highest laser frequency investigated, 0.94
au. In this case both RMT and HELIUM are used to calculate the energy spectrum. The RMT calculation is
based on dipole expectation values, the HELIUM on acceleration expectation values. The results are typical
of those presented in the previous sections. The acceleration based calculations have the lower backgrounds
(and evidently lower errors) at the higher frequencies. Qualitative agreement is observed over a range of 9
orders of magnitude.
|
|
Figure 6 displays the results of a more direct comparison of the RMT and HELIUM integrations than the
results shown in Fig. 5. In Fig. 6 the laser pulse characteristic are the same as those of Fig. 4, but in
the case of Fig. 6 only the Fourier transforms of the dipole expectation values are shown. To
obtain the good agreement between RMT and HELIUM observed in Fig. 6 the RMT inner region
required a much larger basis set of splines than originally anticipated. The RMT integration used
48 splines in a 20 atomic unit inner region, which effectively supports inner region excitations
as high as 300 au in energy. The RMT outer region used a spatial grid point spacing of 0.166
atomic units, and a maximum angular momentum (single-electron) of 6 ℏ. The RMT outer region
Hamiltonian was modelled with 9-point finite-difference, correct to 8th order in the grid point spacing.
Grid point spacings larger than 0.166 au caused stability problems in the RMT integration. The
stability problem became apparent when the basis set of 48 rather than 30 splines was used. The
special feature of the larger basis set is the existence of a high energy, high curvature spline that
lies adjacent the outer region boundary. The outer region finite-difference operators sample the
inner near this boundary, and therefore sample wavefunctions modelled by this high curvature
spline. It is likely that the stability problems occur when the finite-differencing is too coarse
to accurately sample the rapid spatial variation supported by the high energy boundary spline.
The HELIUM integration used a spatial grid point spacing of 0.29 au, (which is the standard setting in
HELIUM). The integration was repeated with a grid point spacing of 0.20 au with no significant change in
results. The HELIUM integration used the same maximum angular momentum as the RMT outer region.
|
|
Figure 7 compares the HELIUM and RMT predictions of g(ω). In this case (5 photon ionisation) both the
HELIUM and RMT integrations use basis sets with peak angular momentum (single-electron) of 8 ℏ. The
RMT integration again used 48 splines in the 20 atomic unit inner region, spatial grid point spacings of 0.166
atomic units in the outer region. Figure 8 compares the single-electron ionisation rates predicted by the
HELIUM with those of the RMT integration. As in the case of two-photon ionisation (Fig. 6), the integration
did not converge until at least 48 basis splines were used in the inner region. A 64 spline inner region basis
gave the same results as 48 splines. The 64 spline basis allowed excitations as high as 600 au in energy, twice
that of the 48 spline basis. The HELIUM and RMT prediction of ionisation yield at the end of the pulse differ
by under 5%, which is roughly the expected uncertainty in both of the numerical integrations.
|
|
|
|
We conclude with the 390 nm results, the longest wavelength used in this series of tests. 390 nm is of
considerable experimental interest because it is readily obtained from frequency doubled Ti-Sapphire 780 nm
lasers. In Fig. 9 we see the first indication of a broad plateau of harmonic peaks, a phenomenon that makes
HHG of such interest and potential value in experimental study. Again there is striking agreement between
the two methods over a range of 12 orders of magnitude. A small but interesting discrepancy between the
results is evident in the 5th and 7th harmonics. Recent calculations of these spectra, [21], shed some light
on this discrepancy. All of the results presented here use the simplest RMT model of helium,
called a 1-state model, in which the final-state residual ion (He+) is restricted to its 1s ground
state. The more recent calculations, [21], exploit a more sophisticated model called the 3-state
model, in which the final-state residual He+ ion can be not just in its 1s ground state, but also
in the two most likely excited states. The 3-state model calculation is more computationally
laborious, perhaps by an order of magnitude, but the 3-state results exactly match those of HELIUM
in the 5th and 7th harmonics, identifying the likely source of the discrepancy. It is interesting
that as RMT approaches HELIUM in the quality of its results, it also approaches HELIUM in
computational overhead. The Fig. 9 HELIUM result required about 6 hours on 4000 cores of
HECToR. The 1-state RMT integration was at least an order of magnitude faster than HELIUM,
but not the 3-state calculation. The great advantage of RMT is that it can be applied to more
complex many-electron atoms like neon and argon, which are in common use by experimentalists.
|
|
|
|
Acknowledgements: This project was funded under the HECToR Distributed Computational Science and
Engineering (CSE) Service operated by NAG Ltd. HECToR - A Research Councils UK High End Computing
Service - is the UK’s national supercomputing service, managed by EPSRC on behalf of the participating
Research Councils. Its mission is to support capability science and engineering in UK academia. The
HECToR supercomputers are managed by UoE HPCx Ltd and the CSE Support Service is provided by NAG
Ltd.
[1] van der Hart HW, Lysaght MA & Burke PG Phys. Rev. A 76 043405 (2007).
[2] van der Hart HW, Lysaght MA & Burke PG Phys. Rev. A 77 065401 (2008).
[3] Guan X, Noble CJ, Zatsarinny O, Bartschat K & Schneider BI Phys. Rev. A 78 053402 (2008).
[4] Lysaght MA, Burke PG & van der Hart HW Phys. Rev. Lett. 101 253001 (2008).
[5] Lysaght MA, van der Hart HW & Burke PG Phys. Rev. A 79 053411 (2009).
[6] Lysaght MA, Burke PG & van der Hart HW Phys. Rev. Lett. 102 193001 (2009).
[7] van der Hart HW & Burke PG (the adaptation); Burke VM, Noble CJ, Plummer M & Burke PG (RMATRIXII/RM95): both to be submitted to Comput Phys Comm.
[8] Nikolopoulos LAA., Parker JS & Taylor KT Phys. Rev. A 78 063420 (2008).
[9] Cavalieri AL et al Nature 449 1029 (2007).
[10] Uiberacker M et al Nature 446 627 (2007).
[11] Drescher M et al Nature 419 803 (2002).
[12] Mauritsson J et al Phys Rev Lett 100 073003 (2008).
[13] Kajumba N et al New J. Phys. 10 025008 (2008).
[14] Baker S et al Science 312 424 (2006).
[15] Baker S et al Phys Rev Lett 101 053901 (2008).
[16] Gordon A et al Phys Rev Lett 96 223902 (2006).
[17] Lysaght MA, Moore LR, Nikolopoulos LAA, Parker JS, van der Hart HW & Taylor KT, ’Ab initio methods for few- and many-electron atomic systems in intense short-pulse laser light’ Quantum Dynamic Imaging: Theoretical and Numerical Methods, editors. A.D. Bandrauk and M. Ivanov (2011).
[18] Moore LR, Lysaght MA, Nikolopoulos LAA, Parker JS, van der Hart HW & Taylor KT, submitted to J. Mod. Opt. (2010)
[19] Smyth ES, Parker JS & Taylor KT Comput Phys Comm 144 1 (1998).
[20] Parker JS, Doherty BJS, Taylor KT et al Phys Rev Lett 96 133001 (2006).