1. Introduction
Electron-atom and electron-ion scattering data are essential in the analysis of important physical phenomena in many scientific and technological areas. These include the development of environmentally safer alternatives to replace mercury vapour lighting, laser-produced plasmasas sources for next-generation nanolithography tools, the understanding of atmospheric processes, diagnostics of impurities in fusion plasmas and the quantitative interpretation of astrophysical data. In addition, the EU (and STFC-CLF) HiPER project (http://www.hiper-laser.org) for laser-ignited fusion, with associated experiments in laboratory astrophysics, opacity measurements, laser-excited hollow atoms and atoms in strong magnetic fields will stimulate detailed calculations of atomic scattering data. Despite the importance of these applications little accurate collision (theoretical or experimental) data is available for many complex atoms and ions. In particular this is the case for electron impact excitation and ionization at intermediate energies near the ionization threshold.
The R-matrix method [1] is an ab initio variational solution to the Schrödinger equation (and its relativistic extensions) for electron-atom (and molecule) scattering problems. Configuration space is partitioned by a sphere containing the target atom (molecule) or ion, outside of which the target wavefunctons are negligible and exchange may be neglected. Inside the sphere an all-electron configuration interaction (CI) treatment produces a ‘full’ set of eigen-solutions for the system, independent of the scattering energy. The energy-dependent R-matrix is formed on the surface of the sphere from the eigenvalues and surface amplitudes of the inner region solutions. Outside the sphere many coupled differential equations must be solved for the scattering electron with multipole potentials derived from the inner region CI target expansion. The R-matrix matches the inner and outer region solutions. Excitation of high-lying ‘intermediate energy’ states and ionization is allowed for by the inclusion of square-integrable ‘pseudostates’ representing high-lying excited states and positive energy states inside the sphere [1]. An alternative intermediate energy treatment (currently for one-electron atoms) extends the radius of the sphere and propagates solutions in partitioned blocks until the two electrons are matched to a large, long-range pseudostate basis [2]: at this large radius a ‘standard’ outer region R-matrix code is required to finish the calculation.
2. Description of software
2.1 The PRMAT package and the
PFARM code
Over the last thirty years a suite of
programs based upon the R-matrix approach has been developed and has enabled
much accurate scattering data to be produced [1].
However, many problems of importance are not practical with programs
designed to run serial computers, and a suite of parallel time-independent Schrödinger equation Fortran
95 codes for electron-atom scattering, PRMAT, funded by EPSRC, has been
designed and implemented [3]. PRMAT is one of the application packages required
to be provided on the UK’s National Supercomputing Services HECToR [4]and HPCx[5],
and consists of RMATRX2/95, based on the serial code RMATRX2 [6], and PFARM,
based on the serial code FARM (Flexible Asymptotic R-matrix Package) [7].
RMATRX2/95 performs the inner region calculations. PFARM uses the results from
RMATRX2/95 to form the energy-dependent R-matrix, then solves coupled
differential equations over all scattering channels by propagating this matrix
outwards from the sphere and matching the solutions to asymptotic boundary
conditions, hence producing the required scattering data in both
individual-atom and, after integration over energy, temperature dependent form.
For complex atoms solutions are required for a dense set of scattering
energies. The PRMAT package has been used to calculate data for electron
collisions with various ions of Fe, Ni, Sn and neutral O. It is also being used
for studies of intermediate energy scattering by light atoms [8].
Recently the PRMATpackage has been extended to include relativistic effects
(needed for detailed treatment of open d-shell atoms and ions, for example)
with the practical effect that the number of scattering channels in PFARM for
systems of interest may now be much larger than for which the code was
originally designed. This is also the case for intermediate energy scattering
in which very large numbers of channels arise from a discretized electronic
continuum inside the sphere. In addition, the complexity of the resonance
structure for low energy electron scattering requires cross sections to be
determined at typically tens of thousands of scattering energy values in order
to yield accurate effective collision strengths.The aim of the
DCSE project is to improve parallel performance of the PFARM code and develop a
more computationally speculative, future-proof (ie deliberately investigating
Fortran 2003 features) code FARM2 which uses a much more memory-efficient
propagator.
As noted above, the PRMAT
package is for electron atom (ion) scattering. In early 2009 a five-year
Software Development Grant was awarded to four collaborating institutions: Queen’s
University Belfast, UCL, the Open University and STFC CSE, to bring together
expertise in all the various areas of ab initio theoretical electron atom and
molecule scattering and both time-independent and time-dependent laser atom
(molecule) interactions. Over the course of this project ‘UK-RAMP’,which
started in October 2009, a unified set of molecular R-matrix codes (UKRmol-in
and UKRmol-out) will be built up using the best features of current codes and
extending them,introducing features from the 2-elecron direct time-dependent solution
code HELIUM for laser assisted ionization and other interactions [9]. The
UK-RAMP project is also extending the HELIUM techniques to cope with general
atoms in a laser field, using the time-independent R-matrix inner region data
as ‘starter’ input. UK-RAMP does not include any development of field-free
time-independent inner region atomic codes as the aim is to build up, optimize
and unify the molecular inner region codes to at least the current level of the
atomic codes, at the same time building up a general set of time-dependent
codes for laser interactions. However, one specific aim of the molecular part
of UK-RAMP is to adapt the PFARM code to accept input data from the
(fixed-nuclear) UKRmol-in molecular package and produce appropriate output data
following calculation of basic scattering parameters. This is timetabled to
take place following this DCSE project and will allow the range of PFARM
calculations to be expanded to diverse electron-molecule scattering
interactions, with many scattering channels and fine grids of energies and/or
inner region nuclear configurations.
2.2The PFARM Code at the start of
the project
PFARM divides ‘external’ configuration space into radial sectors as
shown in Fig. 1 and solves for the Green’s function within each sector using a
basis expansion. This approach is based upon the Baluja-Burke-Morgan (BBM)
method [10].
In this implementation a
variant of the BBM method is used to solve the coupled second-order
differential equations defining the external region scattering. R-matrices at
successively larger radial distances are obtained using Green’s functions
defined within finite radial sectors. The Green’s functions are obtained using
a shifted-Legendre basis.
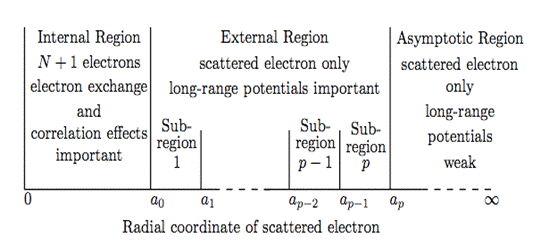
Figure 1. Partitioning of Configuration Space in PRMAT
PFARM
takes advantage of standard highly optimized parallel numerical library
routines and uses MPI for message-passing. The calculation proceeds in two
distinct stages called EXDIG and EXAS.
In
EXDIG, the Hamiltonian in each sector is generated and diagonalized in a
distributed data parallelization, once only for all energies, using the
ScaLAPACK library routine PDSYEVD. The sector Hamiltonians are diagonalized
consecutively using all allocated processes.
The
machine is then reconfigured with groups of processes assigned to specific
tasks for EXAS, as shown in Fig. 2. The production group of processes RMPROD (R-matrix
Production) calculates the initial R-matrix at the internal region boundary for
successive scattering energies. The propagation group of processes RMPROP forms
a systolic pipe along which the stream of R-matrices is passed as they are
propagated from the internal region boundary to the external region boundary.
The pipeline unit is replicated across the machine: three such pipelines are
shown in Fig. 2. Asynchronous non-blocking messages are used to pass R-matrices
between the nodes in the propagation pipeline. At the end of the pipeline the
asymptotic group of processes RMASY (Asymptotic Region Calculation) generates
asymptotic solutions and matches them to the propagated R-matrix to calculate
the scattering K-matrix and collision strengths for transitions between all the
states included in the R-matrix expansion for the current scattering energy. The
RMASY tasks also form partial integrals over energies to convert the collision
strengths to functions of temperature. Finally a single process is dedicated to
gathering the results from the asymptotic group and combining the integrals. Results
are stored to disk periodically to provide a restart procedure, as runs
involving many thousands of scattering energies may take considerable time.
Significant
savings in computation time and memory requirements in EXAS are also obtained
by taking advantage of decoupling of channels in the external region, partitioning them into two non-interacting
groups according to target spin (non-relativistic calculations) or to the
intermediate-coupling K quantum number (for relativistic calculations). In
the most favourable cases this has the effect of splitting the problem into two
roughly equal sized parts. For each block, separate pipelines exist, though the
propagation of the block-split R-matrices across sectors is coupled and some
message passing between processes is required for each equivalent sector calculation.
This decoupling is represented in Fig. 2 by the two rows of processes within a
pipeline.
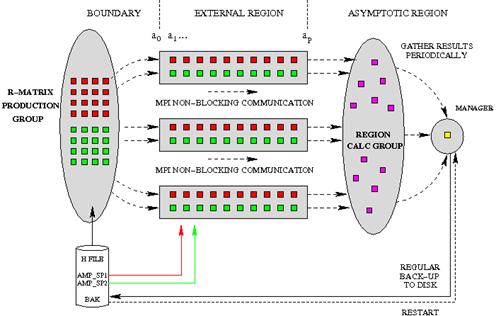
Figure 2. Original assignment of tasks to sub-groups of processes in the EXAS stage of PFARM
A further reduction in compute
time can usually be obtained by undertaking EXAS runs in two stages. Firstly a fine region propagation involving
scattering energies residing in the extremely complex scattering resonance
region followed by a coarse region propagation
for scattering energies above this region. This partitioning allows us to
optimize sector length for each region: generally smaller numbers of sectors with
a larger number of basis functions in the fine region and larger numbers of sectors
with a smaller number of basis functions in the coarse region (see [3] for
details). In most cases the vast majority of energy points lie within the fine
region and therefore this is the stage where most compute time is spent.
The
particular advantages of the parallelization are:
·
The costly parallel diagonalization of
large sub-region matrices is computed independently of scattering energies.
This is particularly suitable for calculations involving hundreds or thousands
of scattering energies.
·
The sub-region propagation calculations
make much use of Level 3 serial BLAS matrix-multiply routines. The highly
optimized BLAS library routines are typically designed to take advantage of the
underlying microprocessor architecture, and therefore attain near peak performance.
Fig. 3, taken from a single-node efficiency study on HPCx [11], shows that PFARM
is one of the fastest application codes, averaging >35% of peak performance,
or 2.1 Gflops/s.
·
On most high-end computing platforms
asynchronous non-blocking communication reduces communication costs.
·
The approach scales well provided computational load is
adequately balanced across functional groups. The number of processes assigned
to functional groups RMPROD and RMASY must ensure that i) initial R-matrices
are generated with sufficient frequency to maintain a fully operational
pipeline; ii) collision strength calculations are processed at a sufficient
rate to prevent bottlenecks.
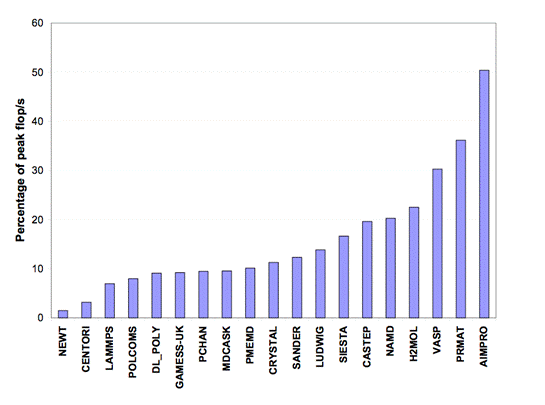
Figure 3. Single Node Performance of PFARM (labelled here as PRMAT) on HPCx
2.3 HECToR distributed-CSE
projects
In 2008 the PRMAT package developers were awarded a contract for Distributed Computational Science and Engineering (dCSE) on HECToR, funded by NAG (Numerical Algorithms Group) Ltd on behalf of the UK Engineering and Physical Sciences Research Council (EPSRC) [12]. The aim of dCSE projects is to enable computational specialists to:
·
port their codes onto
HECToR, in particular to work with new codes or to enable previously
unsupported features in existing codes;
·
improve the performance and
scaling (ideally to thousands of cores) of their codes on HECToR;
·
re-factor their codes to
improve long-term maintainability;
·
take advantage of
algorithmic improvements in the field of high-performance computing.
The
award is to be used entirely for software development in order to increase code
performance and/or utility, and hence to deliver further science. In the case
of PRMAT the project has two main aims: optimization and enhanced
paralellization of PFARM, plus development and incorporation of a new code
using an Arnoldi log-derivative (ALD) propagator [13]. The ALD code implies a
significant improvement in memory efficiency and, once fully incorporated,
performance improvement. The standalone new code deliberately investigates and
experiments with the use of new features of Fortran 2003 as an exercise in
long-term maintainability. The code improvements described in the following
sections have been undertaken as part of this project.
3. Description of Target Hardware
HECToR
HECToR [4] is the UK’s latest National
Supercomputing Service, located at the University of Edinburgh and run by the
HPCx consortium. The HECToR Phase 1 Cray XT4 system (2007 – summer 2009) comprised1416 compute blades, each of which has 4 dual-core
processor sockets. This amounts to a total of 11,328 cores, each of which acts
as a single CPU. The processor is an AMD 2.8 GHz Opteron. Each dual-core socket
shares 6 GB of memory, giving a total of 33.2 TB in all. The theoretical peak
performance of the system is 59 Tflops/s. HECToR Phase 2a (2009 – summer 2010)XT4 comprises 1416
compute blades, each of which has 4 quad-core processor sockets. This amounts
to a total of 22,656 cores, each of which acts as a single CPU. The processor
is an AMD 2.3 GHz Opteron. Each quad-core socket shares 8 GB of memory, giving
a total of 45.3 TB over the whole XT4 system. The theoretical peak performance
of the system is 208 Tflops.positioning
the system at No. 20 in the November 2009Top 500 list [14].
HPCx
For comparison purposes we will also
present results from HPCx [5], the previous UK National Capability Computing
service, located at the Computational Science and Engineering Department at
STFC Daresbury Laboratory [15] and comprising of 160 IBM eServer 575 nodes. Each eServer node contained 16 1.5 GHz POWER5
processors, giving a total of 2536 processors for the system. The total main
memory of 32 GBytes per frame was shared between the 16 processors of the
frame. The frames in the HPCx system were connected via IBM’s High Performance
Switch. The final configuration had a
theoretical peak performance of 15.4 Tflops.
4. Initial performance of PFARM on the XT4
An Initial Performance analysis of PFARM was undertaken on HECToR using an FeIII test case dataset with jj-coupling (ie taking into account relativistic effects). This dataset is representative of recent work by users of PFARM. The propagation involves 1181 channels (equivalent to the dimension of the R-matrix), 10677 scattering energies in the fine region and 205 scattering energies in the coarse region. The version of PFARM used is compiled with the –fast option of the PGI compiler on the XT4 but otherwise is not optimized specifically for the XT4.
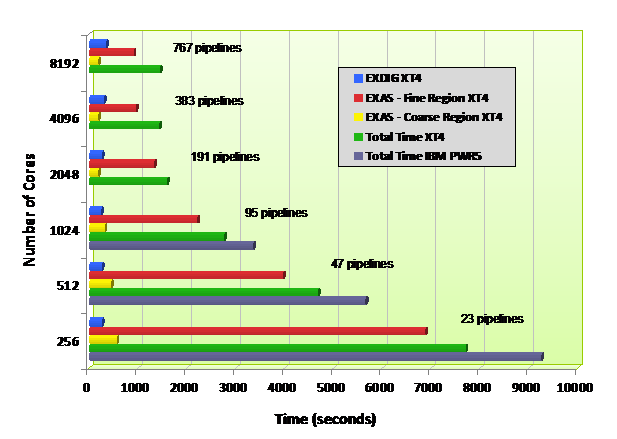
Figure 4. Initial parallel performance of PFARM on HECToR (2008) & HPCx
The timings for the various core counts on XT4 are broken down into the three stages - EXDIG, EXAS Fine Region and EXAS Coarse Region. Summing these times gives the total time taken for the complete external region calculation for this test case. For comparison, total time taken on the HPCx machine (IBM PWR5 p5-575) is included. The spin-split sector Hamiltonian matrix dimensions in EXDIG are 7230 and 4580. The number of pipelines built for the fine region calculation is also shown in Fig. 4. This number rises almost linearly as the number of cores is increased as more pipelines are fitted into the arrangement shown in Fig. 2. It is shown that the fine region propagation scales well up to 2048 cores. This stage usually dominates overall compute time and thus total time also scales well up to 2048 cores. The code continues to speed-up when run on 4096 cores, but no further gains are made by running on 8192 cores. The speed of the coarse region propagation does not improve when running on more than 2048 cores. This is due to the maximum number of pipelines (68) having been reached for the limited number of scattering energies (205) in the coarse region.
5. Optimization of PFARM external region codes on the XT4
Fig. 4 demonstrates that the original EXDIG stage of the program was not scaling well on the XT4. Although this behaviour has little impact on overall time on lower core counts, EXDIG is accounting for around 24% of total run time on 8192 cores. Previous investigations [2, 16] have shown that parallel diagonalization is often a computational bottleneck in large-scale calculations and that parallel scaling is often limited even when using optimized numerical library routines.
5.1 Initial Analysis of Parallel
Diagonalization Routines on the XT4
Several parallel eigensolver routines for solving standard and generalized dense symmetric or dense Hermitian problems are available in the current release of ScaLAPACK [17]. Previous investigations [16] on HPCx had found that the divide-and-conquer-based routine PDSYEVD [18] was most suited to parallel diagonalizations in PFARM, where all eigenpairs of the system are required.
Recently a new routine PDSYEVR [199], based on a Multiple Relatively Robust Representation approach,has been implemented by ScaLAPACK developers. This routine has been made available to users for early testing.
The relative performance of PDSYEVD and PDSYEVR on the XT4 and IBM p5-575 machines is shown in Fig. 5. The performance on lower core counts is roughly equivalent. However the established PDSYEVD routine performs much better on higher core counts and it was decided to continue with this routine. It should be noted that the PDSYEVR routine tested here is under development and any official release is likely to have improved performance. If these scaling issues are resolved then PDSYEVR is likely to be an attractive future option as this method promises much-reduced memory overheads compared to PDSYEVD, allowing larger cases to be solved on smaller core counts.
The performance of PDSYEVD on Hamiltonian sector matrix sizes ranging from N=20064 to N=62304 is shown in Fig. 6. As expected larger problem sizes scale much better as these cases are characterised by a more favourable communication/computation ratio.
The initial performance comparison of the two diagonalizers was undertaken during Phase 1 of Hector. The working version of PDSYEVR suffers from load-imbalance at high core counts. Therefore, until this issue is addressed by the developers, the conclusion that PDSYEVD is the more suitable diagonalization routine for EXDIG remains valid for subsequent upgrades to the service.
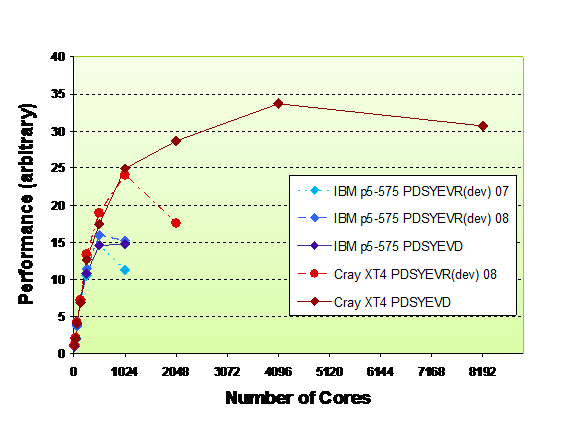
Figure 5.ScaLAPACK Parallel Diagonalizer Performance
on HPCx (IBM p5-575) and HECToR Phase 1 (XT4) for FeIII case with Hamiltonian dimension N = 220064.
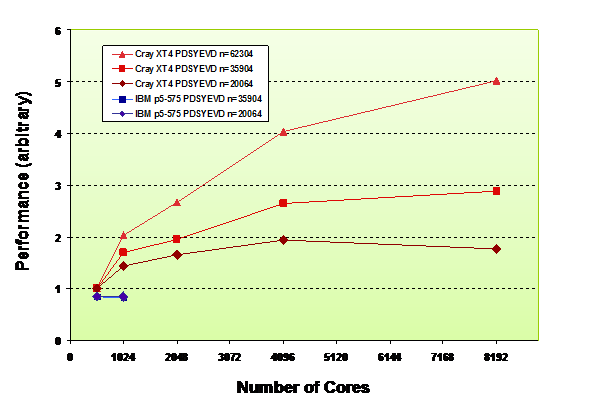
Figure 6. PDSYEVD Performance on HECToR Phase 1 (XT4) and HPCx (IBM p5-575) and for FeIII cases with a range of Hamiltonian dimensions.
5.2 Optimization of EXDIG on the
XT4
The original EXDIG code steps through each sector sequentially, undertaking a parallel diagonalization on each sector Hamiltonian matrix. In order to improve the parallel performance of EXDIG the code has been modified to calculate each Hamiltonian sector parallel diagonalization concurrently on sub-groups of processes. These sub-groups are created by partitioning the global Blacs-based grid. The sub-groups need to be of sufficient size to accommodate the Hamiltonian sector matrix plus associated overheads but small enough to maintain an advantageous communications/computation ratio. Overall this strategy avoids distributing computational loads too thinly when problem sizes are relatively small and parallel jobs involve thousands of cores, i.e. it shifts the parallel scaling behaviour towards the steeper gradients associated with the lower-to-medium core counts in Fig. 5 and Fig. 6. As each sub-group now writes results concurrently to disk, parallelism is also introduced into I/O operations, further improving parallel performance. It should be noted that this new approach involves extra distribution and set-up costs.
The performance improvements on HECToR for an FeIII case with a larger Hamiltonian dimension is shown in Fig. 7. This particular comparison was made on HECToR Phase 1, however the final performance comparisons for our main test case in section 6, which are noticeably better (as may be expected for a smaller Hamiltonian size), show that the results carry through to HECToR Phase 2a. In the new version of the code the four Hamiltonian sector matrices are distributed to four sub-groups of cores of size NP / 4, where NP is the total number of cores. In this case, using the optimized EXDIG code results in a more than two-fold increase in speed on 8192 cores of the XT4. The EXDIG modifications described here will ensure that ambitious calculations planned by PFARM users, with more complex and longer-range potentials and thus involving large sector matrices and more sectors (hence more subgroups as required), will scale well to much larger numbers of cores than this example.
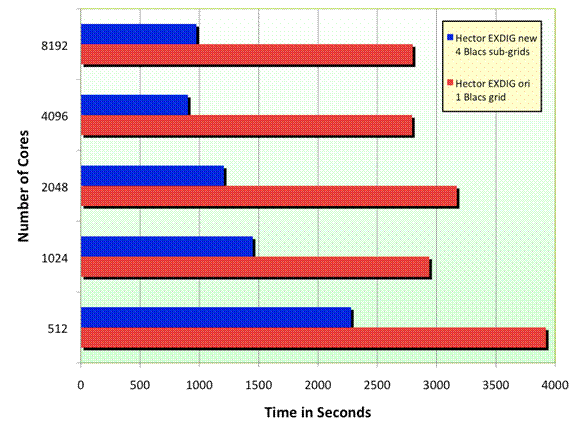
Figure 7. Optimized parallel diagonalization performance on HECToR Cray XT4, Sector Hamiltonian Dimension = 44878.
5.3 Optimization of EXAS on the
XT4
Our major performance optimizations for EXAS are the introduction of new communicators, within the RMPROD group and for multiple manager tasks, together with scripts to ensure optimum load-balancing. In the original code, one group leader gathers together the partial R-matrices, puts them together and distributes them to the pipelines in round-robin order. Our load-balancing analyses showed that as core count increases, the supply of R-matrices to pipelines is too slow and at very high core counts the supply of asymptotic data overloads the manager. We describe our load-balancing investigations and communicator development in chronological order here, followed by a summary of certain other improvements at the end this section. We note that PFARM has built in timing routines which in EXAS allow very detailed timing information for the various concurrent and sequential tasks to be displayed, including the MPI routines. Accurate information from the internal timers is often easier to read and modify (expand upon) than use of the MPI counters in CRAYPAT, and has the advantage of minimizing overheads. However, we were able to discover a bug in the timer routines which caused some of the timing data to overlap and overwrite other parts. We corrected this bug to get accurate internal timings.
5.3.1 Load-Balancing for the XT4
Initial Load-balancing experiments on Hector
Appropriate allocation of processes to
tasks in EXASis critical for efficient parallel performance. Most importantly, the RMPROD and RMASY groups at the start and
ends of pipelines must be of sufficient size to i) generate initial R-matrices with
sufficient frequency to maintain a fully operational pipeline; ii) process collision
strength calculations at a sufficient rate to prevent bottlenecks at the end of
pipelines.
A load-balancing analysis was previously
undertaken on the Manchester Cray T3E (2001) when the PFARM code was initially
developed. Computational experiments that varied the number of processes in the
task groups were reported in publications such as [3]. These now needed to be
updated for the XT4 in order to reflect modern multi-core MPP architectures.
Figure 8 summarises a series of test runs undertaken on the XT4 with 1024 cores
for an energy-reduced fine region propagation. The number of cores in the
RMPROD pool is varied from 224 to 320 and the number of cores in the asymptotic
task group per pipeline is varied
from 2 to 9. It is shown that the
ideally balanced configuration for this case is 288 cores in RMPROD and 7 cores
in RMASY per pipeline. This optimized configuration results in a 28% reduction
in run-time when compared to the worst load-balanced configuration (320 cores
in RMPROD and 2 cores per pipeline in RMASY).
Applying this load-balancing
configuration to the initial full fine region propagation runs from Fig. 4
resulted in the performance improvements shown in Fig. 9. The improved
load-balancing continues to have a substantial impact on speed on 2048 cores,
but the gains are negligible on 4096 cores and 8192 cores. For these cases
further analysis was necessary, but the profiling information indicated that the
single manager process is the bottleneck for 4096 cores and above. The
profiling information also indicated a large MPI_WAIT time for RMPROD tasks
while the group leader communicated with the pipelines.
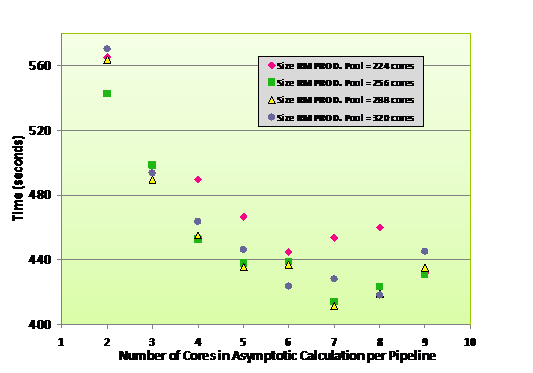
Figure 8. Load-balancing analysis on Hector Cray XT4
Automation of load-balancing on Hector using control scripts
Job control scripts written in Perl have been written that will help determine process allocations automatically, based upon the problem characteristics and the underlying hardware, and these have been updated for HECToR usage. The scripts check a pre-existing database to establish the computational characteristics of the job(s) to be run, e.g. number of channels, the evenness of the channel splitting and then configure the sizes of the functional groups appropriately. These calculations are based upon equations determined from the flop counts of the underlying algorithms which estimate computational loads for each functional group relative to dataset size and number of tasks. Thus for a given dataset and overall core count an estimated rate of initial R-matrix production, R-matrix sector propagation rate and asymptotic calculation rate can all be determined. Taking into account the scalability of each sub-group task, the rates can then be balanced by assigning the appropriate number of cores to each sub-group (table 1). A full description of the evolution of the underlying load-balancing algorithms is given in [3]. During the dCSE project the scripts have been updated to reflect the computational characteristics of the underlying Hector hardware and also have been adapted to include the new features and parallelisation methods introduced into the EXAS code. These new developments to the code are described in detail in the next section.
|
Total Tasks |
RM Production Tasks |
Pipeline Tasks |
Asymptotic Tasks |
Manager Tasks |
|
1024 |
40 x 4 |
288 |
568 |
8 |
|
2048 |
44 x 8 |
568 |
1120 |
8 |
|
4096 |
44 x 16 |
1140 |
2244 |
8 |
|
8192 |
44 x 32 |
2288 |
4488 |
8 |
|
16384 |
44 x 64 |
4576 |
8976 |
16 |
Table 1. Automated core to task configurations for the FeIII dataset
The scripts require two parameters to be set by the developer/user for a particular machine, based on load-balancing experiments. This is enough to give good performance, although users may modify (or request developers to modify) the parameters for fine-tuning EXAS when a large set of runs for a particular scattering problem are to be undertaken. We have set the parameters for HECToR Phase 2A and we will need to reset the parameters for HECToR Phase 2B. Fine tuning of scripts and associated parameters with a range of problem sizes will continue in order to obtain optimal auto-load balancing for users.
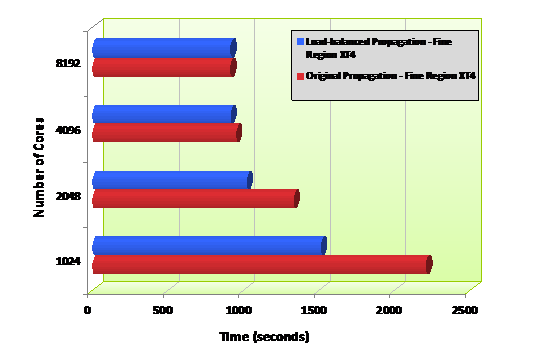
Figure 9. The initial effect on performance of load-balancing EXAS for the fine region propagation
5.3.2 Parallelization of functional groups
Decomposition of R-matrix Production Groups into sub-groups
Performance analyses of EXAS parallel performance on Hector showed that initial R-matrix production rate did not increase linearly with the number of tasks dedicated to this group. Furthermore, for runs involving large numbers of propagation pipelines the supply of initial R-matrices could not match demand from the pipelines even when a large proportion of tasks were dedicated to this functional group, causing pipeline computation to stall. The reasons for the lack of scalability observed in this functional group were twofold. Firstly the parallel computation of initial R-matrices involves an MPI_GATHER operation to combine contributions from the distributed matrix. The performance scalability of these MPI_GATHER operations declines on large core counts. Secondly a serial bottleneck existed where the one ‘leader’ task gathered initial R-matrices, before communicating them to initial pipeline tasks. In practice, the overhead of sending initial R-matrices in sequence to each pipeline from an individual ‘leader’ task became prohibitive when many hundreds of pipelines were waiting. In order to address these bottlenecks, the initial RMPROD communicator was divided into sub-communicators. Ideally the sub-groups should be of such a size that a) sufficient memory and processing power is contained within them to handle the large reduced-width amplitude matrices that are used to generate initial R-matrices, b) MPI_GATHER operations remained efficient and c) sufficient sub-group leader tasks exist in order to communicate initial R-matrices efficiently to the header pipeline tasks.
In addition to the multiple R-matrix generation groups, in the spin/k-split
case we rearranged the distribution of tasks between split blocks to match the relative
sizes of the blocks, rather than equally as in the original code. This improved
the R-matrix generation time noticeably (for example, 1783s v1894s for the main
FeIII test case with 1024 cores, fine propagation with the original RMPROD
setup).
Parallelization of Manager Tasks
For runs involving thousands of cores internal EXAS timers on HECToR began to show a communication bottleneck at the point where the manager task gathers results from the asymptotic (K-matrix calculation) sub-group. The manager task then applies the thermal averaging across the scattering energy spectrum and then periodically outputs results to disk. Originally the code had been designed with the assumption that the maximum number tasks in the asymptotic sub-group would be of the order 200. However on runs involving many thousands of cores of HECToR, the number of pipelines can now regularly exceed 1000, with several tasks in the asymptotic group dedicated to each pipeline. This resulted in pipelines stalling, as the manager task was overwhelmed with outstanding messages emanating from the asymptotic region calculation. Evidently, the manager task role needed expanding to become a manager task sub-group, where a number of manager tasks could share theburden of gathering data, periodically averaging results withthe other manager tasks. A ‘head’ manager is then responsible for outputting backup and final results to disk. This parallelisation has been introduced to the new code (see Fig 10.). The number of manager tasks is determined by user-defined entry in the control file. In our analysis to-date, a ratio of 1 manager task per 500 total tasks usually suffices. Without this new scheme, performance scaling for EXAS would not be possible for more than 2048 cores. It has a significant impact on parallel performance at higher processor counts.
Parallel read of pipeline sector data
The separation of surface amplitude sector files in EXDIG naturally parallelizes output during the first stage of the calculation. Likewise, the separation presents an opportunity to parallelize input to the sector pipelines in EXAS for both the fine region and coarse region calculations with EXAS. The old code used the first task of the first pipeline for all input of sector amplitude files. The new code uses each task in the first pipeline to read its associated sector amplitude file. Associated performance gains are modest at lower processor counts, but have more effect on higher core counts: pipeline set-up times are now 55% faster on 16384 cores of Hector.
Summary of new communicators
Figure 10 shows a simplified version of the current sub-task distribution
and may be compared to figure 2. We note that the MPI-1 is used for all
communication. This made the RMPROD sub-group communicators more complicated to
implement than was originally thought, in order to maintain the order of
energies expected by the RMASY group from the pipelines. Since the number of
pipelines per RMPROD sub-group is not necessarily a factor of the number of RMASY
tasks per pipeline or vice versa, information associated with the RMPROD
sub-group communicators needed to be passed to the pipeline communicators and
the RMASY communicator. The multiple-manager communicator also needs to share
information, but only with the RMASY communicator (assuming the RMPROD
information has been passed correctly). When passive remote memory access and
MPI-2 become generally availablein an efficient form, this hard-wired linking
of ‘internal’data between communicators should no longer be necessary. The
FARM2 code is designed to be adaptable for such communication patterns.
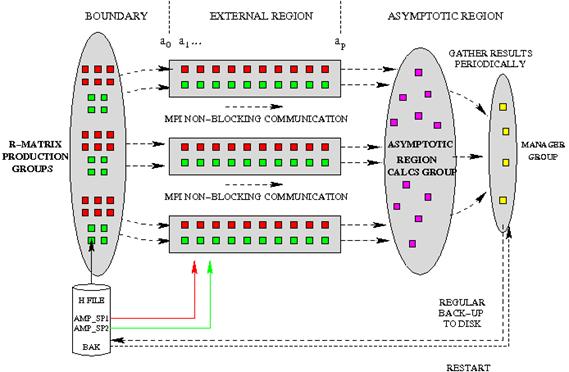
Figure 10. New assignment of tasks to sub-groups of processes in the optimized EXAS stage of PFARM
Shared Memory Processing
Large-scale calculations involving many thousands of channels may produce Hamiltonian matrices or sector R-matrix calculations with memory requirements exceeding that available on a single core of Hector. In these cases it will be necessary to access the full memory resources available on a Hector quad-core cpu from a single MPI task. This can be achieved by under-populating Hector nodes via the #PBS –l mppnppn keyword in the Hector submission script. In order to make use of the other cores an OpenMP enabled version of libsci is linked to the code:
module load xtpe-barcelona
-lsci_quadcore_mp (on the
compiler command line).
The keyword #PBS –l mppdepth is then specified in the job submission script. This instructs the program to spawn OpenMP tasks when the code enters libsci library routines such as Scalapack, Lapack and Blas. For example, the following set-up specifies 1024 MPI tasks in total, with 1 MPI task per Hector node, each of which spawns 4 OpenMP tasks upon entering libsci routines.
#PBS
–l mppwidth = 1024
#PBS
–l mppnppn = 1
#PBS –l mppdepth=4
…
aprun
–n 1024 –N 1 –d 4 ./exas
Analysis from calculations using executables linked tolibsci_quadcore_mp (libsci v10.4.1)show that only modest performance gains are obtained on HECToR. Runs with 4 OpenMP threads are only around 10-15% quicker than those with one OpenMP thread set per quad-core node. Discussions with libsci developers suggest that better performance will be gained from an upcoming release of the library on HECToR.
At the time of writing, the imminent upgrade to HECToR is Phase2b. The new hardware will include nodes with 12 cores sharing the same memory space. On this new hardware, the strategy will be to use as few cores per MPI task that ensures sufficient memory availability for each MPI task.
5.3.3 Other Optimizations
Blas-based K-matrix calculation
One of the important features of EXAS is that the majority of
cpu-intensive serial operations are cast as BLAS and LAPACK routines to
maximize performance. We confirmed this by profiling the code with CRAYPAT,
however we noticed that the routine 'kmm' in module 'k_matrix' showed up as
having significant cpu activity. The k-matrices, produced by the RMASY group,
are the basic desired scattering parameters from which physical quantities of
interest are calculated. Inspection of routine kmm showed that, while the bulk
of the calculation involved a LAPACK singular value decomposition (SVD), there
were some handwritten loops preceding this with inner 'if' statements and
multiply-adds which could be rearranged to be performed as two DGEMM
operations. Implementing this resulted in up to a 20% improvement in serial
performance for k-matrix generation.
Time limit failsafe from PBS script
A
common problem for many application code users is the estimation of run-time required
for calculations involving a given number of cores. Although a user is free to set
a maximum wall-clock time (12 hours) for every job submitted, in practice this
would usually have a detrimental impact on throughput, especially when using a
large, shared compute facilities such as Hector. Given the wide range of
problem sizes associatedwith different partial waves in a complete scattering
calculation, it can be particularly difficult for PRMAT users to estimate upper
limits on likely run times. In order to minimise wasted runs a check-pointing
facility was incorporated into the original code, where users could specify the
frequency of check-points to disk through input parameters. This scheme indeed
safeguarded results. However, too frequent checkpoints could impact upon performance,
whilst too infrequent checkpoints ran the risk of losing significant amounts of
results data when wallclock limits were reached unexpectedly. Simple perl
scripts have now been developed to establish time limits from the PBS
environment and use this value automatically in the code to schedule a
checkpoint shortly before wall-clock limits are reached. This frees the user
from estimating likely run times and removes the need for frequent
check-points. Users still have the option to specify regular checkpoints from
the input control file. This is advisable during periods of machine
instability.
Verification of results
Verification of results was based upon a FeIII JJ-coupling case (Partial Wave L,S,P=3,0,0). Results from 1024, 2048, 4096 core runs on the original and final versions of the code were compared and thermally averaged collision strength results matched to at least 7 decimal places for values of the order 10-1. These slight variances are expected due to the new developments sometimes changing the order of calculations. The results were also verified against those obtained from HPCx.
6. Final PFARM Benchmarking Results from
Hector Phase 2A
Description of Benchmark Dataset
FeIII case with JJ coupling,
Partial Wave L=3, S=0, P=0
Computational Characteristics
|
Number of Channels (spin-split) |
723,
458 |
|
Maximum Scattering Energy |
2.5 |
|
Fine Region Energy Grid Resolution |
0.00004 |
|
Number of Fine Region Scattering Energies |
10678 |
|
Coarse Energy Grid Resolution |
0.01 |
|
Number of Coarse Region Scattering Energies |
205 |
|
Initial Radius |
25.0 |
|
Final Radius |
80.0 |
|
Number of Fine Region Sectors |
4 |
|
Number of Coarse Region Sectors |
9 |
|
Fine Region Hamiltonian Dimension (spin-split) |
7230*,
4580* |
|
Coarse Region Hamiltonian Dimension (spin-split) |
7230,
4580 |
Table 2. Computational
Characteristics of the benchmark dataset
* A suitable combination of basis functions and sector
boundaries to ensure accuracy is determined automatically by a pre-existing
algorithm in EXDIG. Number of basis points function in the fine region sector
Hamiltonian lies between a minimum of 10 and a maximum determined by the user. Number
of basis function points in the coarse region sector is always set to 10.
Parallel Performance Final Benchmarks
The final
benchmarking analysis was undertaken on Phase 2A of the HECToR Cray XT4 system.
Both the original and new codes are compiled using the PGI compiler (v9.04)
with optimization flags ‘-O2 –fast’(for PFARM, -O2
did not improve performance). Timings from the codes are measured via calls to
the Fortran intrinsic routine system_clock. A typical benchmarking submission script is
listed below. It should be noted that HECToR nodes were fully occupied
throughout these tests, i.e. 1 MPI task per available core.
#!/bin/bash
#PBS -N prm_bench_1024
#PBS -l mppwidth=1024
#PBS -l mppnppn=4
#PBS -l walltime=01:00:00
#PBS -j oe
#PBS -A c01-am
cd $PBS_O_WORKDIR
export NPROC=`qstat -f $PBS_JOBID | awk '/mppwidth/ {print
$3}'`
export NTASK=`qstat -f $PBS_JOBID | awk '/mppnppn/ {print
$3}'`
# Sector Diagonalization
aprun -n $NPROC -N $NTASK ./exdig
# Fine Region Propagation
aprun -n $NPROC -N $NTASK ./exas
# Coarse Region Propagation
aprun -n $NPROC -N $NTASK ./exas
The final benchmark timings are shown in Fig 11 below. Both the
original ‘ORI’ and optimized ‘NEW’ versions of the code were compiled and
benchmarked on the HECToR Phase2A system as of April 2010. For a range of core
counts between 1024 and 16384, the ‘NEW’ HECToR optimized codes runs between
2.14 and 2.89 times faster than the original ‘ORI’ codes, with performance
gains steadily improving as the core count increases. The ‘MIXED’ timing
dataset shown in Fig 10 refers to a benchmark run where a different number of
cores are chosen for each of the three stages of the calculation. This is often
the case in users’ production runs, where the largest core counts are selected
for EXDIG and EXAS Fine Region calculations (where a calculation typically
includes tens of thousands of scattering energies), but it is often more
appropriate to use much smaller core counts for EXAS Coarse Region
calculations. The ‘MIXED’. Here 4096 cores are used for EXDIG, 8192 cores are
used for the EXAS Fine stage and 512 cores are used for EXAS Coarse. This gives
a speed-up of 3.13 between the new and original codes.
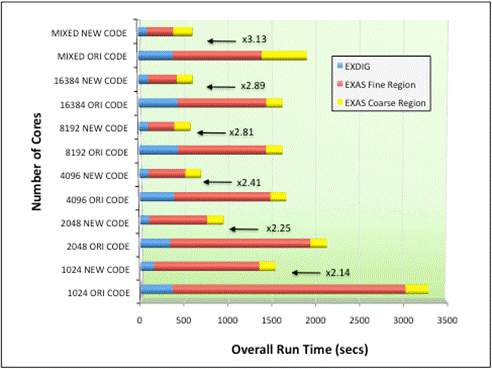
Figure 11. Benchmarks comparing Hector performance of final PRMAT code with that of the initial code
In order to assess the new codes’ performance on future, larger datasets, which are representative of users’ planned calculations, a further benchmarking exercise was undertaken on an enlarged version of the FeIII benchmark dataset described in Table 2. Here the number of scattering energies in the EXAS Fine Region is almost doubled to 21080 and 28 basis function points are used when constructing the spin-split Fine Region Sector Hamiltonians. This led to matrices of dimension 20244 and 12824 requiring diagonalization during the EXDIG stage of the calculation. With this expanded dataset on 8192 cores the (NEW) optimized codes are 2.35 times faster than the (ORI) original codes’. This speed-up increased to 2.58 with the MIXED case, where 8192 cores are used for EXDIG & EXAS Fine and 512 cores are used for EXAS Coarse.It should be noted that although the code optimizations achieved during this project are directed at larger-scale calculations, the load-balancing for this case has not yet been as completely fine-tuned as for our main test case. We believe that this is the reason that performance gains so farare less than the 3.13 demonstrated for the original FeIII dataset.
7. FARM2: the ALD code
The second part
of the dCSE project has been dedicated to introducing the ALD propagator into the
PRMAT. ALD is a stable propagation
method for solving coupled sets of Schrödinger equations introduced by
Alexander and Manolopoulos [13]. Within each sector the potential coupling the equations is approximated
by a linear reference potential. An optimum reference potential is obtained by
diagonalizing the full potential coupling matrix at two points defined by a
Gauss integration mesh scaled to the radial sector. Exact solutions of the
sector equations with a linear reference potential are given by Airy functions.
These may be computed accurately and efficiently. The size of matrices
associated with Airy LD propagations is much reduced in comparison with the BBM
approach, at the expense of needing more sectors, and ALD is expected to
maintain better performance at capability usage for larger problems. Since the
log-derivative solutions matrix is propagated rather than the R-matrix (the two
are proportional to each other’s inverses), the channel splitting (spin or K)
is maintained across the sector boundaries is this method, modifying the pipeline
communication in the parallel case. In fact, since the matrices involved are
much smaller (a factor of 10 for the case of 10 BBM basis functions s described
above), it is possible to keep both partitions on the same core, or for larger
calculations, use shared memory multicore parallelism for the splitting. The
R-matrix at the inner region boundary is inverted, solutions are propagated to
the asymptotic region where K-matrices and other scattering results are
generated (to maintain consistency with FARM/PFARM, the R-matrix may be
reconstructed and passed to standard asymptotic modules).
The method has been introduced into a new
object-oriented (within Fortran 2003 limits) version of FARM, namedFARM2, which
also incorporates the mixture of symmetry-based block-partitioned and
block-diagonal matrices directly into the propagation procedure via appropriate
use of derived datatypes. The parallelization of this code includes an
efficient customized parallel I/O library. Much of the effort in this part of
the project has gone into developing efficient lower-level functional modules,
deliberately experimenting with Fortran 2003 features, as FARM2 is designed to
be future-proof. Not all these features are yet available as standard on most
compilers: the NAG compiler version 5.2 copes with all the Fortran 2003 syntax,
but for example does not actually implement asynchronous I/O. This compiler has
been used to test the code on HECToR, with the Intel compiler used on a local
machine. For practical purposes while we wait for compilers to catch up, the
ALD propagator is being introduced as an alternative to BBM in a hybrid version
of PFARM. At the conclusion of the project this hybrid is being verified: the
advantages are that EXDIG data for all the sectors is not needed and the much
larger number of sectors allows for more flexible pipeline parallelization
(without boundary communications). The ALD version of PFARM will be completed
as a full user code as part of the UK-RAMP project.
We now give a summary description of the lower-level
functional modules: full descriptions and details will appear in the full
write-ups for Computer Physics Communications (CPC).
7.1 xstream: a library for
data transfer within and between programs
The fundamental idea motivating the development of this module was to
provide a simple and uniform API for performing the file I/O operations used
throughout the R-matrix programs. This is used (a) to transfer data between
computational modules and (b) to hold large data structures that are employed
within a single program stage. In case (a) the primary requirement is to be
able to transfer binary encoded files between different computers and computer
architectures. This implies that the encoding within the disk files themselves
should be in XDR format. This in turn requires the use use of C-language code
to call standard unix system encoding/decoding routines. The API is designed to
allow the use of either XDR or native files with implementation details hidden
from the user. We have also invested effort to ensure that the C-code operates
correctly for both iLP32 and LP64 architectures. The C-interoperability
provided by Fortran 2003 provides a portable and standard way of interfacing
this code to the R-matrix routines written in Fortran. It should be noted that
very high performance is not essential for this type-(a) I/O. For the second type of disk I/O, type (b), performance
is essential. One priority is parallel performance. We have therefore developed
both serial and parallel modules using the same API. The parallel I/O is implemented
using MPI-IO. Files may be read/written
simultaneously by all processing nodes or all nodes may write to a single file.
We use non-blocking MPI calls to allow asynchronous I/O and stream-IO to locate
data items within the file. In the serial version of this option Fortran 2003
asynchronous I/O is used to hide data transfer times. Although most Fortran compilers
now do provide stream I/O, this was not the case when this development began.
We have therefore offered stream I/O implemented in C.
These libraries provide a range of serial and parallel options without
the need to implement alternative coding options each time file I/O is
required. They have a fairly simple calling syntax compared to more generalized
products such as netCDF (http://www.unidata.ucar.edu/software/netcdf/docs/faq.htm). On
HECToR and other HPC machines they will mainly be used for data transfer
between the various R-Matrix modules (purpose (a)): the internal I/O is
available as an option and for local machines). We note that PFARM uses XDR as
its standard format for initial and inter-stage datafiles.
7.2 Block matrix algebra
In all R-matrix external region calculations the angular momentum
coupling rules require the scattering channels to decouple into one or two
groups, or partitions, that are coupled by the external region interaction only
within their own partition. For instance, in the case of LS coupling, the two
partitions are labelled by a target spin. A similar decoupling occurs for
relativistic Jpi coupling. Of course, if there are two partitions, they are
coupled by the boundary condition at the R-matrix internal region boundary.
Nonetheless, this decoupling has important consequences both on storage
requirements and on CPU requirements. In
the present implementation we fully exploit these possibilities and show that
they may be significant for large calculations.
The immediate consequence is that the coupling potential is block
diagonal and should be stored as a block diagonal matrix. Using the algebra of
2x2 block matrix inversion it is possible to make large savings in CPU. The present implementation must provide
alternative code segments if a particular calculation involves one are two
channel partitions. Some initial work using the Fortran2003 object oriented
features suggests that defining a matrix class that is extended to a
two-partition block-diagonal matrix can reduce the detailed logic by the use of
dynamic dispatch.Without this refinement, the savings obtained in transforming
to a sector representation (see below) and in propagating the logarithmic
derivative matrix using channel decoupling open the way to the very large
coupled equation solutions (20000 channels) that are currently required. The
log-derivative solutions matrix is stored in a derived type for block-symmetric
matrices in which the diagonal blocks and the upper off-diagonal block are
stored as separate matrices: Schur decomposition is used to perform, for
example, matrix inverses.
At a more prosaic level we have tested the performance
of Lapack routines that may be used for linear equations solution and matrix
inverses: The standard dgetrf/dgetrs
routines, the routines dsytrf/dsytrs
for symmetric matrices and singular value decomposition (SVD) for possibly
singular matrices. The SVD routines take ~8 times as long as the LU
factorization routines as may be expected, and should only be used when needed.
However, for a given set of linear equations or matrix inverse there is no
advantage in using the symmetric dsytrf/dsytrs
routines, which may in fact take longer than the general matrix dgetrf/dgetrs routines. This is due to
the greater use of dgemm operations
in the general matrix routines which is more efficient than the multiple use of
dgemvin dsytrf/dsytrs and compensates for the overall greater number of
operations in the general routines, except in the limit of very large matrices
(sizes up to 5000 have been tested). All three options are available in the
FARM2 codes, with SVD used very selectively withtests for its requirement in
the code, and dgetrf/dgetrs as
standard.
7.3 AiryGrid and AiryProp:
the ALD propagator.
The solution of
the coupled second-order differential equations describingthe electron-atom
scattering in the region beyond an inner interactionregion where coupled
integro-differential equations apply may be performedusing various propagation
techniques. These numerical methods propagate the solution of the dfferential
equations between two radial distances,an inner and outer point, where boundary
conditions may be determined.In the BBM method the radial range is divided into
radialsegments or sectors. Within each of these sectors a basis set is
introducedto represent the local Hamiltonian. By diagonalizing this local
sectorHamiltonian it is possible to derive a set of linear equations
forproducing the solution and its derivative at one end of the sectorgiven the
corresponding values at the other end. The BBM approachis formulated in terms
of R-matrices that are simply the inverse oflogarithmic derivative of the
wavefunction at each radial point.The introduction of a large sector basis
permits large sector sizesso fewer sectors are required in the overall
calculation. The methodmay be made very accurate and is particularly
well-suited when thenumber of collision energies that must be treated is very
large, hence its use up to now in PFARM. Unfortunatelyas the sector matrices
that must be diagonalized have dimensions thatare the product of the number of
coupled channels and the number ofbasis functions introduced. As the number of
coupled channels is increased,the best available parallel matrix diagonalizers
begin to scale lesswell and the amount of data that is involved in the
calculation increasesrapidly. This effectively limits the number of channels
that may betreated.
The ALD method
developed by Alexander [13] is a complementary approachthat bypasses the
bottleneck imposed by the efficiency of paralleldiagonalizers. The basic idea
isto assume that the potential within each sector may be diagonalizedand
approximated by a linear potential (the linear reference potential).The method
is a generalization of a scheme. albeit formulated in termsof R-matrices,
proposed by Light and Walker (LW) [20] which uses a constantreference
potential. In the ALD scheme the reference potential maybe chosen to match the
actual potential at two radial points withineach sector. If these two radial
points are chosen to correspond tothe roots of the second-order shifted
Lagendre polynomial the method
will be exact
for potentials that may be approximated by a 2nd -3rd
order polynomial [13]. The LW and ALD methods share two advantages: thematrices
that must be diagonalized are the same order as the numberof channels and the
propagation equations within each sector involvevectors rather than matrices
(and may be cast in the form of matrix operations on diagonal matrices). The
amount of data that must be retainedbetween each calculation is minimal and the
matrices correspondingto even 20-30 thousand scattering channels may be
diagonalized usingonly a small number of processors. The solutions of the
sector equationsare trigonometric functions in the LW method and Airy functions
inthe ALD scheme. Manolopolous and Alexander [13] have shown that the
Airyfunctions and derivatives may be calculated without significantly more
effort than trigonometic functions. The ALD is thereforemore efficient than LW
and although smaller sectors will be requiredthan in the BBM approach massively
parallel HPC machines may be usedto treat much larger numbers of channels. In
addition, as the ALDis ‘potential following’ there is no requirement to treat
resonanceregions differently from regions where there are no resonances.
In the current FARM2 implementation of ALD,
the routine AiryGrid controls the determination
of the outer radial distance to which propagation needs to be performed and
sets up the grid of sectors. It forms the block-diagonal potential matrix which
is diagonalized within each sector: essentially it fulfils the equivalent
function to EXDIG and constructs all energy-independent quantities which are
then stored either in memory or using xstream.
The routine AiryProp performs the
actual ALD propagation using the block-partitioned matrix syntax and passes
data to the FARM2 asymptotic routines.
7.4 Channel dropping
Although the R-matrix and Log-Derivative matrix propagation techniques
are extremely stable it is possible for the differential equations sets to
become linearly dependent. This behaviour is a consequence of the physics of
the collision process itself. In the region beyond but near the R-matrix
internal region boundary it is essential to introduce additional channels in
the external region calculation to account for polarization and other effects
resulting from the electron-target interaction. These additional bound channels
do not carry scattering information and indeed cause the linear dependence that
results in the failure of the linear equation solvers used to perform the
sector propagation. We have introduced
linear equation solvers using the Lapack SVD routines that will maximize the
accuracy of calculation within a given sector. However, in cases where the
propagation proceeds over a number of sectors these redundant channels
introduce exponentially growing errors. It is therefore essential to actually
eliminate the channels as the propagation proceeds. Such a channel-dropping
procedure was implemented in the serial FARM external region code. However, it
has been found that in practice some of the restrictions used in the FARM
implementation are too limiting. First, within a given sector only a single
channel could be dropped and second, it is possible that channel-dropping could
be blocked by the detailed way in which coupling strength criteria were
applied. We have therefore implemented a more general approach in which any
number of channels may be dropped. Blocking is eliminated and the energy
criterion for determining channels to be dropped is based on the channel
eigenvalues.
The channel dropping procedure itself is performed easily and
efficiently in FARM2 using BLAS routines and Fortran pointers. The process,
when needed, is implemented separately within each channel partition. As a
consequence the bookkeeping needed to track and reassemble the retained
channels in order to complete the K-matrix calculation is more complicated than
in previous work.
7.5 Asymptotic functions and some general points
The
FARM2 code also features a new implementation of the Gailitis asymptotic
expansion [21] of the wavefunction at the external matching point: these
changes are the result of a detailed analysis of the numerical stability of the
method using the CPC package [21]. The new approach avoids cancellation in the
division of two ‘Burke-Schey’ series [21] by the use of standard Lapack
routines. The new approach is of higher accuracy than that used previously.
Having matched the propagated matrix with the asymptotic solutions, various
scattering parameters (K-matrices, collision strengths etc) are calculated.
Following this DCSE project, with the propagator and general solution validated
by extensive comparisions with known calculations, the FARM2 code is undergoing
rigorous verification of the asymptotic scientific data generation procedures.
The overall design of the FARM2 code is tofacilitate a rapid parallelization
using combined MPI and shared memory (System 5) parallelization [22], with
pipelining (MPI, ideally using passive remote memory access) and multicore
parallelism within the block-partitioned matrices, in addition to the parallel xstreamI/O. We note that the modules in
FARM2 have been tested and verified for numerical stability using the CADNA
instrumentation package [23].
7.6 Hybrid parallel code and results
Towards the end of the DCSE project and as immediate follow-up work, the AiryGrid and AiryProp modules have been introduced into a hybrid ALD PFARM EXAS code, using PFARM parallelization methods. The AiryProp procedure fits into the pipeline group of cores, with several ALD sectors propagated on each core. The AiryGrid set-up work is carried out on these processors while the RMPROD processors receive the initial R-matrix data (the best way of incorporating the AiryGrid set-up is being investigated). Both partitions are propagated on a single core at present: the multicore shared-memory parallelism will be introduced in both the hybrid code and the ‘pure’ parallel FARM2 ‘simultaneously’.
At the time of writing, the validation of the hybrid interface to AiryGrid and AiryProp is underway. We will add initial performance comparisons for an FeIII case to this report as soon as they are available.
8. Future work on PFARM and the ALD code
In addition to ongoing tasks indicated in the previous section, further potential optimizations to PFARM have been identified, although development of the new communicators was given priority for this particular DCSE project.
Further improvements include:
1. Greater
flexibility in the assignment of sectors to processes. The code was originally
designed for architectures with memory resource per process a small fraction of
that available on HECToR. This resulted
in a programming model where each pipeline process is always designated one
spin-split sector calculation regardless of problem size and memory
availability. With target calculations now increasing by up to an order of
magnitude, this rigid mapping needs to be relaxed in order to permit:
a)
More than one process per sector
calculation (for larger jobs), achieved via a data distribution parallelization
of the R-matrix sector propagation, i.e. pipeline nodes compromising of groups of processes.
b)
More than one sector per process (for
smaller jobs) in order to fully utilize local memory resources and reduce
communication overheads.
Both these aims are effectively near completion
from the development of the hybrid code.
2.
An assignment of tasks to processes that
reduces communications between the underlying hardware. For example on HECToR,
neighbouring sectors should reside within a multi-core processing element
whenever possible. This will be particularly important for HECToR Phase 2B and
beyond (Again, this is built into the FARM2 and hybrid code structure).
3.
Fine-tuning of
auto-loadbalancing scripts on HECToR Phase 2B.
4. The
introduction of task-harnessing to calculate different groups of partial waves
and energies concurrently. The process arrangement shown in Fig. 2 would be
replicated across HECToR resources for each, or groups of, partial waves
(scattering symmetries) and energies associated with the calculation.
5. Further
parallel I/O features (full incorporation of the xstream library) will be introduced into the PFARM code where
appropriate.
Further
work on FARM2 involves completing the verification of the ALD scattering
parameter code against a range calculations and adding various additional
scientifically relevant final data derived from the scattering parameters.
Also, the hybrid code needs load-balance analysis and the ‘pure’ parallel FARM2
code needs completing/validating, though this latter objective requires the
implementation of Fortran 2003 on general hardware to ‘catch up’ with the
coding.
9. Conclusions
In this paper we have described some of the optimizations being undertaken on the parallel R-matrix program PFARM for runs using the Cray XT4. The code combines a unique, highly flexible functional and data decomposition approach for external region R-matrix propagation.The code is built on highly optimized parallel numerical library routines and is therefore highly efficient. However modifications to the code need to be made in order to maximise performance on the new generation of high-end computing resources, typically with many thousands of multi-core processors. Improvements to parallel scaling performance, single-node efficiency and memory usage will enable very large electron-atom and electron-ion scattering calculations to be addressed on these machines. The PFARM code may also be reasonably straightforwardly adapted for outer region electron-molecule scattering. We have demonstrated that code optimizations undertaken to-date have already yielded significant increases in performance of the code on the XT4.
We have developed a ‘future-proof’ code FARM2, deliberately reliant on Fortran 2003 features. The ALD propagator has been incorporated into the PFARM parallel structure.
The earlier part of this project has been reported on for the 2009 Cray User Group Meeting [24]. We aim to make all the fully verified codes available through the CCPForge website [25] and through the Computer Physics Communications (CPC) program library, with associated peer-reviewed fully descriptive CPC articles. The dCSE project was for 12 months FTE (inclusive of weekends, leave etc), split between two people (AS and CJN) between June 2008 and March 2010.
Acknowledgments
The authors would like to thank the following colleagues and collaborators for their contributions to this work:
Val Burke, STFC Daresbury Laboratory
Phil Burke, Queen’s University Belfast
Christof Voemel, ETH Zurich
Penny Scott, Queen’s University Belfast
Cathy Ramsbottom, Queen’s University Belfast
About the Authors
Dr Andrew Sunderland(andrew.sunderland@stfc.ac.uk) is a computational
scientist in the Advance Research Computing Group, Computational Science and
Engineering, at STFC Daresbury Laboratory. His work involves the development,
optimization and analysis of scientific codes and parallel numerical
algorithms.
Professor Cliff Noble (cliff.noble@stfc.ac.uk) is a visiting professor at the Department of Computational Science and Engineering at STFC Daresbury Laboratory. His previous role was Head of the Atomic and Molecular Physics Group in the department. The focus of his work is developing codes that calculate atomic and molecular collision processes using high performance computers.
Dr Martin Plummer (martin.plummer@stfc.ac.uk) is a computational scientist and Group Leader for Theoretical Atomic and Molecular Physics in the Advanced Research Computing Group, Computational Science and Engineering, at STFC Daresbury Laboratory. He also optimized and managed various codes on the UK HPC service HPCx with particular responsibility for the materials science code CASTEP.
All the above authors can be contacted at:
STFC Daresbury Laboratory,
Warrington,
WA4 4AD
United Kingdom
Tel: +44 1925 603000
References
1.
P G Burke,
C J Noble and V M Burke, Adv. At. Mol. Opt. Phys. 54 (2007) 237-318.
2.
NS Scott, MP Scott, PG Burke, T
Stitt, V Faro-Maza, C Denis and A Maniopoulou, Computer Physics Communications (CPC) 180 (2009)
2424-2449.
3.
A G
Sunderland, C J Noble, V M Burke and P G Burke, CPC 145 (2002), 311-340.
4.
HECToR –
UK National Supercomputing Service, http://www.hector.ac.uk.
5.
HPCx – The
UK’s World-Class Service for World-Class Research, http://www.hpcx.ac.uk.
6.
P G Burke,
V M Burke and K M Dunseath, J Phys. B 21 (1994), 5341-5373.
7.
V M Burke
and C J Noble, CPC 85 (1995), 471-500; V M Burke, C J Noble, V Faro-Maza, A
Maniopoulou and N S Scott, CPC 180 (2009), 2450-2451.
8.
BM McLaughlin, MP Scott, AG Sunderland, CJ Noble, VM Burke, CA
Ramsbottom, R H G Reid, A Hibbert, K L Bell, P G Burke, Atomic Data Nucl. Data Tables 93, 55-104 (2007);
M Lysaght, PhD thesis, University College Dublin, Ireland (2006); MP Scott, CA
Ramsbottom, CJ Noble, VM Burke, PG Burke, J Phys B: At. Mol. Opt. Phys. 39,
387-400 (2006); BM McLaughlin, A Hibbert, MP Scott, CJ Noble, VM Burke, PG
Burke, J Phys B: At. Mol. Opt. Phys. 38, 2029-2045 (2005); M Plummer, CJ Noble,
M Le Dourneuf J Phys B: At. Mol. Opt. Phys. 37, 2979-2996 (2004); see also ‘Mathematical
and computational methods in R-matrix theory’, eds. M Plummer, J D Gorfinkiel
and J Tennyson, CCP2, STFC Daresbury Laboratory, UK, 2007 (on line version http://www.ccp2.ac.uk).
9.
JS Parker, BJS Doherty, KT Taylor, KD Schultz, CI Blaga and LF DiMauro,
Phys Rev Lett 96 (2006) 133001.
10.
K L
Baluja, P G Burke and L A Morgan, CPC 27 (1982), 299-307.
11.
Single
Node Performance Analysis of Applications on HPCx, M. Bull, HPCx Technical Report HPCxTR0703 (2007), http://www.hpcx.ac.uk/research/hpc/technical_reports/HPCxTR0703.pdf.
12.
HECToR
– Distributed CSE Support, http://www.hector.ac.uk/cse/distributedcse.
13.
M H Alexander, J Chem Phys 81 (1984) 4510-4516; MH Alexander and D E
Manolopoulos, J Chem Phys 86 (1987) 2044-2050.
14.
TOP 500
Supercomputing Sites,http://www.top500.org.
15.
STFC's Computational Science
and Engineering Department, http://www.cse.scitech.ac.uk/.
16.
Using Scalable Eigensolvers on HPCx: A Case Study, Ian
Bush, Andrew Sunderland, Gavin Pringle, HPCx Technical Report HPCxTR0510 2005, http://www.hpcx.ac.uk/research/hpc/technical_reports/HPCxTR0705.pdf.
17.
The
ScaLAPACK Project, http://www.netlib.org/scalapack/index.html.
19.
PDSYEVR. ScaLAPACK’s parallel MRRR algorithm for the
symmetric eigenvalue problem}, D.Antonelli, C.Vomel, Lapack working note 168,
(2005), http://www.netlib.org/lapack/lawnspdf/lawn168.pdf.
20.
J C Light and R B Walker, J Chem. Phys. 65 (1976)
4272-4282
21.
M Gailitis, J Phys. B 9 (1976); C J Noble and R K
Nesbet, CPC 33 (1984) 399-411
22.
N S Scott,F. Jézéquel, C. Denis and J.-M. Chesneaux,
CPC 176 (2007) 507-521; http://www.lip6.fr/cadna.
23.
see, for, example:http://en.wikipedia.org/wiki/Shared_memory
24.
A G Sunderland, M Ashworth, C J Noble and M Plummer,
Proceedings of the Cray User Group (CUG 2009), Atlanta, Georgia, USA, http://www.cug.org/
25.
http://ccpforge.cse.rl.ac.uk