Improving the performance of
A DCSE project
D. Casterman
The University of Sheffield, Mappin street, S1
3JN, Sheffield
Abstract
This report presents the implementation of a full pencil (stick) decomposition of the 3D FFT for the improvement of the Quantum Espresso (QE) package. This algorithm is compared with the existing plane decomposition algorithm implemented in QE. This new algorithm is intrinsically slower than the previous algorithm for a small number of processors. However, the two algorithms present similar performance for the number of processors equal to the maximum scaling limit of the plane decomposition algorithm which is equal to the number of grid points along the z axis of the 3D function. The pencil decomposition algorithm is also shown to scale up to 1024 processors with a speed-up of 67 % compared to the computational time of 1 processor (A performance which depends on the FFT grid). The improvement of this scalability is of great interest in Quantum Espresso as it will enable users to study larger and more realistic systems, i.e. having a supercell containing more atoms. The algorithm presented in this report can also be transferred to other codes.
Contents
1.1-Presentation
of the project
3.1-Tests
and comparison with previous algorithm..
3.3-Improvement
with 2D virtual grid of processors
1-Introduction
1.1-Presentation of the project
This report
presents the work package 3 of the dCSE project “Improving of the
- Code Familiarisation (2 months). (Completed)
- Isolate code for FFT routine and devise a test set (1 month). (Completed)
- Implement pencil distribution within FFT routines in PW (ie given the existing data distribution do any necessary communication within FFT routines to get data into the new pencil form) (4 months). (Completed)
- Modify data distribution of PW and PH (5 months). (Incomplete)
- Testing and validation (Concurrent with 1-4).
- Report on 3D FFT for knowledge transfer. (Completed)
As a result, this report presents a complete description of the full pencil decomposition for the evaluation of the 3D Fast Fourier Transform (3D FFT) to improve the scalability of the PW and PH codes of the QE package [2]. This full pencil decomposition partially follows the work presented by Jacode and Sigrist [3-4].
The integration of this algorithm in the main PW and PH codes has not been successful as the project ran out of time. Although the data distribution in PW and PH has been modified according to the new algorithm, other errors hampers the the code to run and seems to be too complex to debug or predict within the timescales of this project. The code has been delivered to NAG. All the calculations presented in this report were carried out on the national computer grid facility, HECToR [5].
1.2-Quantum Espresso and GWW
Quantum Espresso
[2] (opEn Source Package for Research in Electronic Structure, Simulation, and
Optimization) is an integrated suite of computer codes for
electronic-structure calculations and materials modelling at the nanoscale. It
is based on density-functional theory, plane waves, and pseudopotentials (both
norm-conserving and ultrasoft) and
implements a range of pseudopotentials and exchange correlation functionals,
including Hartree-Fock and hybrid functionals (PBE0, B3LYP,
- pw.x
(Electronic and Ionic Structure, including MD)
- ph.x
(Phonons using Density Functional Perturbation Theory)
As explained
by I. Bethune [1], Quantum Espresso is written in Fortan 90, consisting of over
300,000 lines of code in nearly 1000 source files. In addition to the source
for each executable, there is a common Modules directory containing code shared
by all the executables. This includes common functionality such as I/O,
parallelisation, data types, as well as the FFT. A number of external libraries
are required including an FFT library (e.g. FFTW3) as well as BLAS, LAPACK and
ScaLAPACK for linear algebra operations.
1.3-Benefits
Quantum
espresso is a widely used code in the scientific community studying condensed
matter physics. The improvement of its scalability is crucial for the study of
more and more complex and realistic structures. Recently, the study of atomic structures
as large as 1200 atoms has been presented in the literature [6]. For such a
system, the computational burden is important and requires the scalability of
the code to 1000s of processors in order to evaluate the relevant properties
such as the band structure of the system. In particular, the GW method has been
shown over the last decades to be the most accurate method to estimate this
band structure as it models correctly the complex interaction between electrons.
However, this method has so far been limited to few atoms as the computational
demand to solve the problem is too important. However, a smart solution and
implementation of this method has recently been added by Paolo Umari to the
Quantum Espresso package making the package of great interest for the entire scientific
community studying the physics of materials.
2-FFT algorithm
2.1-Algorithm
The first step
is to create two sub-communicators Comm_Row
and Comm_column from the standard
communicator MPI_
![]()
! This creates the
subgroup
color1 = (mpirank-mod(mpirank,Ncol))/Ncol
key1 =
mod(mpirank,Ncol)
CALL MPI_
CALL MPI_
! This creates the
subgroup
color2 = mod(mpirank,Ncol)
key2 =
(mpirank-mod(mpirank,Ncol))/Ncol
CALL MPI_
CALL MPI_
![]()
The indices
mpirank, me_row and me_column are respectively the ranks in the communicators
MPI_![]() , is given by the following equation (where mod is the modulo
function),
, is given by the following equation (where mod is the modulo
function),
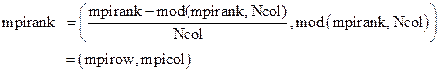 (1)
(1)
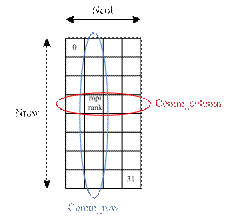
Figure 1. Sketch representing the re-organization of the processors in a 2D Cartesian grid. In this figure, the blue and red ellipses respectively show the sub-communicators Comm_row and Comm_column to which the processor mpirank belongs to.
Having created
the two communicators, the second step is to determine the number of 1D FFTs to
be done by each processor. Ideally, this number should be the same in order to
distribute the workload evenly. To do so, a Np x 4 matrix, called
FFT_Sticks(Np,4), is added in the
fft_dlay_descriptor used in Quantum espresso (Np is the total number
of processors). Here, stick is employed as a synonym of pencil (i.e. a 1D FFT),
and FFT_sticks(:,4) contains all the necessary information
concerning the number of pencils (sticks) carried by each processor between
each MPI_ALLTOALLv call. In order to illustrate this statement, the number of
1D FFT along x carried by the processor mpirank is equal to FFT_sticks(mpirank+1,1)* FFT_sticks(mpirank+1,2).![]()
In this
situation, FFT_sticks(mpirank![]() ,1) is the distribution of z points along one column and
FFT_sticks(mpirank
,1) is the distribution of z points along one column and
FFT_sticks(mpirank![]() ,2) is the distribution of y points along one row. As a
result,
,2) is the distribution of y points along one row. As a
result,
![]() (2)
(2)
where ![]() is the floor function
and
is the floor function
and ![]() is defined as,
is defined as,
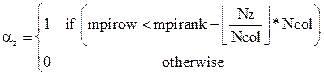 (3)
(3)
Note that ideally ![]() is equal to 0 for all
processors which corresponds to an even distribution of the z points along the
column. In the same way, the distribution of y points along the row is given
by with the following equations,
is equal to 0 for all
processors which corresponds to an even distribution of the z points along the
column. In the same way, the distribution of y points along the row is given
by with the following equations,
![]() (4)
(4)
where ![]() is defined as,
is defined as,
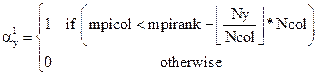 (5)
(5)
In the same way,
FFT_sticks(mpirank![]() ,3) and FFT_sticks(mpirank
,3) and FFT_sticks(mpirank![]() ,4) are given by,
,4) are given by,
![]() (6)
(6)
With,
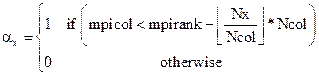 (7)
(7)
And,
![]() (8)
(8)
With,
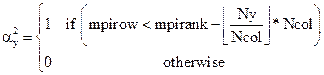 (9)
(9)
This matrix is then employed in the following algorithm which is illustrated in Figure 2 for a 8x16x24 FFT grid. This algorithm can be detailed as,
1) 1D FFT along x
2) Re-sort data
3)
MPI_ALLTOALLv in the sub communicator
4) Unpacking data
5) 1D FFT along y
6) Re-sort data
7)
MPI_ALLTOALLv in the sub communicator
8) Unpacking data
9) 1D FFT along z
In Figure 2, the actions of “re-sorting” and “unpacking” the data are not shown. If a NxxNyxNz grid has to be transformed, the ith processor has a maximum number of elements equal to
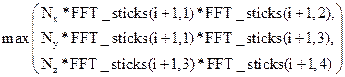 (10)
(10)
To carry out the 1D FFT transformation, a simple plan has been employed and is built by the function, dfftw_plan_dft_1d( ) in FFTW
![]()
type(fft_dlay_descriptor) :: dfft
DO i=0,Np-1
! Number of
z per row
a = int(Nz/Nrow)
dummy1 = ((i-mod(i,Ncol))/Ncol);
dummy2 = (Nz-a*Nrow);
IF(dummy1<dummy2) a=a+1
! Number of
y per col
b = int(Ny/Ncol)
IF(mod(i,Ncol)<(Ny-b*Ncol)) b=b+1
! Number of
x per col after 1st MPI_alltoallv in Comm_column
c = int(Nx/Ncol)
IF(mod(i,Ncol)<(Nx-c*Ncol)) c=c+1
! Number of
y per row after MPI_alltoallv in Comm_row
d = int(Ny/Nrow)
dummy1 = ((i-mod(i,Ncol))/Ncol)
dummy2 = (Ny-d*Nrow);
IF(dummy1<dummy2) d=d+1
!
FFT_sticks save all these data
dfft%FFT_sticks(i+1,1)=a
dfft%FFT_sticks(i+1,2)=b
dfft%FFT_sticks(i+1,3)=c
dfft%FFT_sticks(i+1,4)=d
ENDDO
![]()
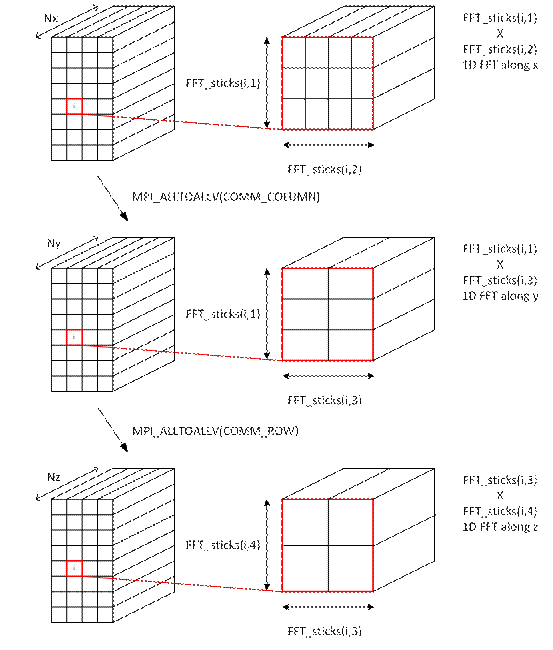
Figure
2. Sketch of the decomposed algorithm
without “re-sorting and unpacking” stages. This figure shows how the
number of FFT sticks per processors is stored in the algorithm using FFT_sticks.
In this example, The grid is a 8x16x24 grid and FFT_sticks(i![]() ,1)=3, FFT_sticks(i
,1)=3, FFT_sticks(i![]() ,2)=4, FFT_sticks(i
,2)=4, FFT_sticks(i![]() ,3)=2 and FFT_sticks(i
,3)=2 and FFT_sticks(i![]() ,4)=2.
,4)=2.
2.2-FFTW
Two different approaches can be employed to evaluate many 1D FFTs. The first one is to create a simple complex-to-complex 1D FFT plan and evaluate a series of FFT using a loop,
![]()
! 1D forward FFT along
x
CALL dfftw_plan_dft_1d(plan,Nx,cin,cout,FFTW_FORWARD,FFTW_ESTIMATE)
! Creation
of a many FFTs plan
DO i=1,(dfft%FFT_sticks(me_p+1,1)*dfft%FFT_sticks(me_p+1,2))
DO j=1,Nx
cin(j)=f(j+(i-1)*Nx)
ENDDO
CALL dfftw_execute(plan) ! Execution of the
plan
DO j=1,Nx
aux(j+(i-1)*Nx)=cout(j)
ENDDO
ENDDO
CALL dfftw_destroy_plan(plan)
! Destruction of the plan
![]()
The second approach is to create a more complex plan for many complex-to-complex ffts. To use this function, one has to understand the notions of stride and distance used as arguments of the function dfftw_plan_many_fft() of the FFTW library.
![]()
nsl=(dfft%FFT_sticks(me_p+1,1)*dfft%FFT_sticks(me_p+1,2))
CALL dfftw_plan_many_dft(plan, 1, Nx, nsl, f(1:), Nx, 1, Nx, aux(1:), Nx, 1, Nx,
FFT_FORWARD,
FFT_ESTIMATE) ! Creation of a “Many FFT” plan
CALL dfftw_execute_dft(plan,f,aux)
! Execution of the plan
CALL dfftw_destroy_plan(plan)
! Destruction of the plan
![]()
The stride and the distance give an insight to the memory pattern employed to store the data. Figure 3(a) and (b) respectively show two different patterns: (a) stride = 1 and dist = NX, and (b) stride = NX and dist = 1. These two stride and dist parameters may be used to reduce the “re-sorting” and “unpacking” data by reorganizing the FFT algorithm.
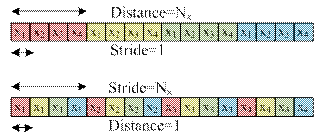
Figure 3. Illustration of the memory pattern for (a) stride = 1 and dist = NX, and (b) stride =NX and dist = 1. The distance corresponds to the difference (in memory) between the first element of one FFT and the first element of the next FFT to be done. Stride is the difference (in the memory map) between the first and the second element for the same FFT.
Having tested the two methods for 50 forwards and backwards FFTs on a 111x143x78 with 64 cores, it was observed that the second approach is faster as it only takes about 0.59s in comparison to 0.66s for the first approach.
3-Performance
3.1-Tests and comparison with previous algorithm
To test the algorithm, a simple sine function has been employed. Two different grids have been used (respectively 128x128x128 and 111x143x78). The last grid enables to check the validity of the MPI_ALLTOALLv call for random grid numbers. Figure 4(a) respectively shows the speedup obtained for the 128x128x128 FFT grid from the pencil and plane decomposition of the FFT algorithm. For this test, 5000 forward and backward FFTs were calculated and the time was recorded as the difference between the beginning and end of this loop. Both algorithms demonstrate similar speed-up, but the pencil intrinsically enables the scaling of the FFT to a greater number of processors. However, looking closely at the computational time, Figure 4(b) shows that the plane decomposition algorithm is faster for a small number of processors but the difference between the algorithms drops off as the number of processors approaches 128, which is the maximum scaling limit for the plane decomposition algorithm applied to this grid. For this particular example (128x128x128), the data are homogeneously distributed on all the processors, i.e. each processor the same number of plane or pencils. However, this is usually not the case and an optimization of the pencil decomposition can be obtained.
A method to achieve this goal is proposed in the section 3.3.
(a)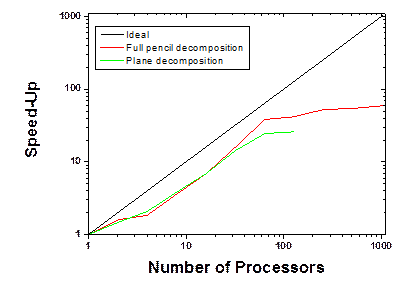
(b) 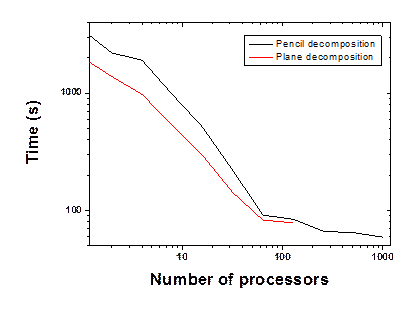
Figure 4. Comparison of the speed-up between the plane decomposition (extracted from the Quantum Espresso package) and the implemented full pencil algorithm. Figure (a) presents the comparison of the speed-up of the two algorithms for a 128x128x128 grid and Figure (b) shows the computational time of these two algorithms for the same grid. The time for 1 processor is evaluated by applying the plane or pencil decomposition algorithm to 1 processor. Note that for the plane decomposition algorithm, the program does not provide the good results when distributed on the number of processors greater the number of points along z, i.e. 128 in this case.
3.2-Accuracy of the results
Before
presenting the optimization of the algorithm, it is important to check the
correctness and the accuracy of the results. For this purpose, Figure 5(a) shows the part of the function carried by
Processor 0 and Figure 5(b) shows the
difference between the original function and the same function after 50 forward
and backward FFTs. This difference is of order 10-14 which is acceptably within the expected round off error for double
precision floating point arithmetic.
(a)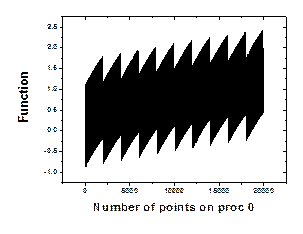
(b) 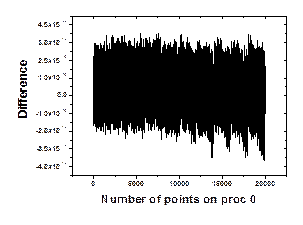
Figure 5. (a) Part of the function carried by proc. 0 (b) difference between the input function and the transformed function after 50 forward and backward FFTs.
3.3-Improvement with 2D virtual grid of processors
The full pencil decomposition requires an organization of the processor as a 2D grid. As a result, an optimization of the algorithm consists in selecting the most adequate 2D virtual grid of processors which satisfy the condition,
![]() (3)
(3)
where Np, Ncol and Nrow are the number of processors, the number of column and row as aforementioned. For each possible 2D grid, the data to be Fourier transformed are distributed in the same way as presented in section 2.1 and consequently, the following calculation can be carried out for each situation,
1) Calculation of the maximum number of pencils (sticks) per processor before each FFT transform (along x, y and z).
2) Evaluation of the weighted mean of these 3 numbers.
The optimal 2D virtual grid of processors is obtained for the distribution which yields to the minimum weighted mean. This method may not be the best but presents good results as it is now presented
Based on this definition, the FFT have been calculated for the two grids 111x143x78 and 128x128x128. The speed-ups evaluated on the best and worst 2D distribution of processors are evaluated for a 111x143x78 grid and presented in Figure 6(a). The best means that the FFT is evaluated on the most adequate 2D virtual grid of processors (minimum weighted mean) while the worst is obtained when the weighted mean is maximum. In Figure 6(a), one can observe that the speed-ups are similar for a small number of processor (lower or equal to 16), but better performances are obtained for Np>16. The difference between the two virtual grids reaches a maximum for 256 processors which demonstrate a speed-up difference of 27%.
Figure 6(b) presents the best and worst speed-ups for the 128x128x128 grid. Independently of these distributions of processors, the FFT sticks are homogeneously distributed, i.e. each processor carries the same number of FFT sticks. As a result, the FFT speed up is independent of the 2D virtual grid of processors.
(a)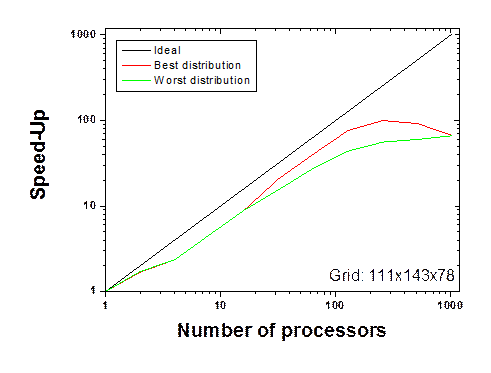
(b)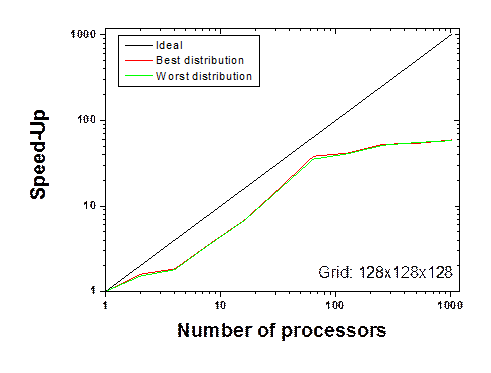
Figure 6. Speed-up of the FFT evaluated on the worst and best 2D virtual grid of processors for (a) a 111x143x78 grid and (b) a 128x128x128 grid.
4-Conclusion
A full
pencil decomposition of the 3D FFT algorithm is presented in details in this
report. This decomposition requires the creation of a 2D virtual grid of
processors which have been optimized to yield better performances (up to 27%
speed-up increase). As expected, this algorithm is slower than the plane
decomposition algorithm already implemented in the quantum espresso package for
small numbers of processors. However, the two algorithms present similar
performances at the maximum scaling limit of the plane decomposition algorithm
(equal to the number of points along the z axis (stick) is in Quantum Espresso),
and the new algorithm is shown to scale up to 1024 processors. Although this
algorithm is applied to QE, it can also be transferred to other codes developed
for various scientific topics outside material science.
The incorporation of this algorithm into the main GWW codebase could not be finished
because of issues encountered in modifying the distribution of the data carried
by each processors, from planes to pencils. The strategy employed for the
integration of the new algorithm was to split the number of points along the y
axis (wherever it is needed) in the main code (consisting of over 300,000 lines
of code in nearly 1000 source files). While it works in isolation, however,
this substitution in each of the identified source files seems insufficient
which implies that more modifications are required at a deeper level of the
code. These modifications appear to be too complex to predict within the
attributed timescales of this project, particularly with scarce supporting
documentation. The debugging also requires a more in-depth understanding of the
relationship between source files and the techniques underlying the physics in
the code. Nevertheless, all the modified source files as well as the algorithm are
available to NAG and QE administrators as required. The work carried out by I.
Bethune shows excellent improvement in comparison to the original
implementation and consequently offers a better performance to QE users.
Acknowledgements
This project
was funded under the HECToR Distributed Computational Science and Engineering
(CSE) Service operated by NAG Ltd. HECTOR – A Research Councils UK High End
Computing Service – is the UK’s national supercomputing service, managed by
EPSRC on behalf of the participating Research Councils. Its mission is to
support capability science and engineering in UK academia. The UK
supercomputers are managed by UoE HPCx Ltd and the CSE Support Service is
provided by NAG Ltd. http://www.hector.ac.uk
References
[1] “Improving
the performance of
[2] Quantum Espresso, http://www.quantum-espresso.org/
[3] Fourier
Transforms for the BlueGene/L Communication Network, Heike Jagode (2006).
http://www2.epcc.ed.ac.uk/msc/dissertations/dissertations-0506/hjagode.pdf
[4] “Optimizing
parallel 3D Fast Fourier Transformations for a cluster of
http://www2.epcc.ed.ac.uk/msc/dissertations/dissertations-0607/2298876-27hd07rep1.1.pdf
[5] HECToR website, http://www.hector.ac.uk
[6] F. Varchon, P. Mallet, J.-Y. Veuillen
, and L. Magaud, Phys. Rev. B 77, 235412 (2008).