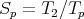Developing Hybrid OpenMP/MPI Parallelism
for Fluidity-ICOM - Next Generation
Geophysical Fluid Modelling Technology
, , ,
,
aAdvance Research Computing Group,
Computational Science & Engineering Department,
Science and Technology Facilities Council,
Daresbury Laboratory, Warrington WA4 4AD UK
bApplied Modelling and Computation Group,
Department of Earth Science and Engineering,
Imperial College London, London, SW7 2AZ, UK
Summary of the Project Progress
In order to further develop Fluidity-ICOM (build upon finite element methods and
anisotropic unstructured adaptive meshing) to run efficiently on supercomputers
comprised of NUMA nodes, mixed mode OpenMP/MPI parallelism has been
implemented in Fluidity-ICOM. Benchmarking has already shown that the two
dominant simulation costs are sparse matrix assembly, and solving the sparse
linear systems defined by these equations. The thread-level parallelism of sparse
matrix assembly kernels has been realised through well established graph colouring
techniques to remove the data dependencies in matrix assembly, which allow very
efficient parallelisation with OpenMP. In the sparse solver we have utilized threaded
HYPRE and the ongoing threaded PETSc branch which results in improved
performance compared to pure MPI version. Various NUMA optimizations have
also been implemented. The profiling and the benchmark results of matrix assembly
on the latest CRAY platforms show that the best performance can be achieved by
pure OpenMP within node.
The following list highlights the major developments:
- Matrix assembly node optimisation can be done mostly using OpenMP with
efficient colouring method, which avoid the use of mutual synchronization
directives: eg. Critical.
- Regarding PETSc Matrix stashing, it does not have any redundant calculations.
However, it does incur the cost of maintaining and communicating stashed
rows, and this overhead will increase for higher MPI process counts. A further
complication of non-local assembly is that the stashing code within PETSc is not
thread safe.
- Local assembly has the advantage of not requiring any MPI communications as
everything is performed locally, and the benchmark results also highlight the fact
that the redundant calculations are not significantly impacting performance when
local assembly is used. Furthermore, the scaling of local assembly is significantly
better than non-local assembly at higher core counts. This makes assembly an
inherently local process. Thus focus is on optimizing local (to the compute node)
performance.
- The current OpenMP standard(3.0), which has been implemented by most
popular compilers, doesn’t cover page placement at all. For memory-bound
applications, like Fluidity-ICOM, it is therefore important to make sure that
memory get’s mapped into the locality domains of processors that actually access
them, to minimize NUMA traffic. In addition to our implementation of first touch
policy, which improves data locality, thread pinning can be used to guarantee that
threads are executed on the cores which initially mapped their memory regions
in order to maintain locality of data access.
- For Fluidity-ICOM matrix assembly kernels, the performance bottle neck becomes
memory allocation for automatic arrays. Using NUMA aware heap managers, such
as TCMalloc, it makes pure OpenMP version outperform the pure MPI version.
- Benchmarking results with HYPRE and threaded PETSc show that mixed mode
MPI/OpenMP version can outperform pure MPI version at high core counts
where I/O becomes major bottleneck for pure MPI version.
- With mixed mode MPI/OpenMP, Fluidity-ICOM can now run up to 32K cores
job, which offers Fluidity capability to solve the ”grand-challenge” problems.
Key
words:
Fluidity-ICOM;
FEM;
OpenMP;
MPI;
NUMA;
Graph
Colouring;
1 The Fluidity-ICOM dCSE project
The Fluidity-ICOM (Imperial College Ocean
Model)
dCSE project commenced on 1st October 2010 and is scheduled to end on the 31st
September 2012. This highly collaborative project also involved Gerard Gorman
from Applied Modelling and Computation Group (AMCG), Imperial College
London.
Fluidity-ICOM
is an open source partial differential equation simulator build upon various finite
element and finite volume discretisation methods on unstructured anisotropic
adaptive meshes It is being used in a diverse range of geophysical fluid flow
applications. Fluidity-ICOM uses three languages (Fortran, C++, Python) and
uses state-of-the-art and standardised 3rd party software components whenever
possible.
Using modern multi-core processors presents new challenges for scientific software
such as Fluidity-ICOM, due to the new node architectures: multiple processors each
with multiple cores, sharing caches at different levels, multiple memory controllers
with affinities to a subset of the cores, as well as non-uniform main memory access
times.
Because of this, there is a growing interest in hybrid parallel approaches where
threaded parallelism is exploited at the node level, while MPI is used for
inter-process communications. Significant benefits can be expected from
implementing such mixed-mode parallelism. First of all, this approach decreases the
memory footprint of the application as compared with a pure MPI approach.
Secondly, the memory footprint is further decreased through the removal of the
halo regions which would be otherwise required within the node. For example, the
total size of the mesh halo increases with number of partitions (i.e. number of
processes). It can be shown empirically that the size of the vertex halo in a linear
tetrahedral mesh grows as O(P1.5), where P is the number of partitions.
Finally, only one process per node will be involved in I/O (in contrast
to the pure MPI case where potentially 32 processes per node could be
performing I/O on Phase 3 of HECToR), which will significantly reduce the
number of meta data operations on the file system at large process counts for
those applications based on files-per-processes I/O strategy. Therefore, the
use of hybrid OpenMP/MPI will decrease the total memory footprint per
compute node, the total volume of data to write to disk, and the total
number of meta data operations given Fluidity-ICOMs files-per-process I/O
strategy.
For modern multi-core architecture supercomputers, hybrid OpenMP/MPI also
offers new possibilities for optimisation of numerical algorithms beyond pure
distributed memory parallelism. For example, scaling of algebraic multi-grid
methods is hampered when the number of subdomains is increased due to
difficulties coarsening across domain boundaries. The scaling of mesh adaptivity
methods is also adversely effected by the need to adapt across domain
boundaries.
Portability across different systems is very critical for application software
packages, and the directives based approach is a great way to express parallelism in
a portable manner. It offers potential capabilities to use the same code base to
explore accelerated and non-accelerator enabled systems because OpenMP is
expanding its scope to embedded systems and accelerators.
Therefore, there is strong motivation to further develop OpenMP parallelism in
Fluidity-ICOM to exploit the current and future architectures.
However, writing a truly efficient OpenMP/MPI scalable OpenMP program is
entirely non-trivial, despite the apparent simplicity of the incremental
palatalisation approach. This paper will demonstrate how we tackle the race
conditions and performance pitfalls during OpenMP palatalisation.
The Fluidity-ICOM dCSE project mainly comprised of three work packages
(referred to as WP1, WP2, WP3), WP1 MPI/OpenMP mixed-mode parallelisation
of the Finite Element Assembly Stage in Fluidity. WP2 Optimizing HYPRE
Library usage for Linear Preconditioners/Solver for large core counts. WP3 Final
benchmarking including using threaded PETSc branch
The remaining part of this report is organised as follows: In the next section we
describe the Fluidity-ICOM matrix assembly and greedy colouring method in
detail. Section 2.2 will address thread safe issues during OpenMP palatalisation
and performance gained by solving these issues. Section 2.5 discusses how we
optimise memory bandwidth which is particularly important for OpenMP
performance. The last section 2.5 contains a conclusion, a discussion about further
work
With these developments, Fluidity/ICOM is now able to exploit HECToR to its
full capacity, and assist in the enabling of our leading-edge technology to tackle
grand-challenge science applications
2 WP1: MPI/OpenMP mixed-mode parallelisation of the Finite Element
Assembly Stage in Fluidity
Previous performance analysis (2) has already shown that the two dominant
simulation costs are sparse matrix assembly (30%-40% of total computation), and
solving the sparse linear systems defined by these equations. The Hypre librarys
hybrid sparse linear system solvers/preconditioners, which can be used by
Fluidity-ICOM through the PETSc interface, are competitive with the pure MPI
implementation. Therefore, in order to run a complete simulation using OpenMP
parallelism, the sparse matrix assembly kernel is now the most important
component remaining to be parallelised using OpenMP. The finite element
matrix assembly kernel is expensive for a number of reasons including:
significant loop nesting, where the innermost loop increases in size with
increasing quadrature; many matrices have to be assembled, e.g. coupled
momentum, pressure, free-surface and one of each advected quantity; indirect
addressing (a known disadvantage of finite element codes compared to
finite difference codes); and cache re-use (a particularly severe challenge
for unstructured mesh methods). The cost of matrix assembly increases
with higher order, and discontinuous Galerkin (DG) discretisations are
used.
For a given simulation, a number of different matrices need to be assembled, e.g.
continuous and discontinuous finite element formulations for velocity, pressure and
tracer fields for the Navier-Stokes equations and Stokes flow. Each of these
have to be individually parallelised using OpenMP. The global matrix
to be solved is formed by looping over all the elements of the mesh (or
sub-domain if this is using a domain decomposition method) and adding the
contributions from that element into the global matrix. Sparse matrices
are stored in PETSc’s (Compressed sparse row) CSR containers (these
includes block-CSR for use with velocity vectors, for example, and DG).
The element contributions are added into a sparse matrix which is stored
in CSR format. A simple illustration of this loop is given in algorithm
1.
|
Algorithm 1. Generic matrix assembly loop
globalt4ht@95xmatrix ← 0
for e = 1 → numbert4ht@95xoft4ht@95xelements do
localt4ht@95xmatrix = assemblet4ht@95xelement(e)
globalt4ht@95xmatrix+ = localt4ht@95xmatrix
end for
|
2.1 Greedy colouring method
In order to thread the assembly loop illustrated in algorithm 1, it is clear
that both the operation assembles an element into a local matrix, and
the addition of that local matrix into the global matrix must be thread
safe.
This can be realised through well-established graph colouring techniques
(3). This is implemented by first forming a graph, where the nodes of the
graph correspond to mesh elements, and the edges of the graph define
data dependencies arising from the matrix assembly between elements.
Each colour then defines an independent set of elements whose term can
be added to the global matrix concurrently. This approach removes data
contention, so called critical sections in OpenMP, allowing very efficient
parallelisation.
Generally, we try to colour as many vertices as possible with the first colour, then
as many as possible of the uncoloured vertices with the second colour,
and so on. To colour vertices with a new colour, we perform the following
steps.
- Select some uncoloured vertex and colour it with the new colour.
- Scan the list of uncoloured vertices. For each uncoloured vertex,
determine whether it has an edge to any vertex already coloured with the
new colour. If there is no such edge, colour the present vertex with the
new colour.
This approach is called ”greedy” because it colours a vertex whenever it can,
without considering the potential drawbacks inherent in making such a
move. There are situations where we could colour more vertices with one
colour if we were less ”greedy” and skipped some vertex we could legally
colour.
To parallelise matrix assembly(1) using colouring, a loop over colours is
first added around the main assembly loop. The main assembly loop over
elements will be parallelised using the OpenMP parallel directives with a
static schedule. This will divide the loop into chunks of size ceiling
(numbert4ht@95xoft4ht@95xelements/numbert4ht@95xoft4ht@95xthreads) and
assign a thread to each separate chunk. Within this loop an element is
only assembled into the matrix if it has the same colour as the colour
iteration.
The threaded assembly loop is summarised in algorithm 2.
Algorithm 2. Threaded matrix assembly loop
graph ← createt4ht@95x graph( mesh,discretisation)
colour ← calculatet4ht@95x colouring( graph)
kt4ht@95x colouring = max( colour)
globalt4ht@95x matrix ← 0
for k = 1 → kt4ht@95x colouring do
independentt4ht@95xelements = {e|colour[e] ≡ k}
for all e  independentt4ht@95xelements do independentt4ht@95xelements do
localt4ht@95xmatrix = assemblet4ht@95xelement(e)
globalt4ht@95xmatrix+ = localt4ht@95xmatrix
end for
end for
|
Generally, the above colouring method tries to colour as many vertices as possible
with the first colour, then as many as possible of the uncoloured vertices with the
second colour, and so on. Therefore the number of elements is not balanced
between each colour group. For OpenMP, its not a problem as long as each thread
has enough work load. The performance is not sensitive to the total number of
colour groups
2.2 Performance Improvement and Analysis for matrix assembly kernels
All performance benchmarks were carried out on the HECToR Cray XE6-Magny
Cours (phase2b) and Cray XE6-interlagos (phase3). The benchmark test case used
here is wind-driven baroclinic gyre. The mesh used in the baroclinic gyre
benchmark test case has up to 10 million vertices; resulting in 200 million degrees
of freedom for velocity due to the use of DG. The basic configuration is
set-up to run for 4 time steps without mesh adaptivity. It hence considers
primarily the matrix assembly and linear solver stages of a model run. The
details of solving equations and configuration can be found in reference
(2).
The momentum equation assembly kernel uses Discontinuous Galerkin methods
(DG) and Continuous Galerkin method (CG) has been parallelised with the
above-mentioned procedures. Several thread safe issues have been solved which
result of a performance gain.
2.3 Local assembly v.s. non-local assembly
In PETSc, when adding elements to a matrix, a stash is used. For parallel
matrix formats this provides one particularly important benefit, namely that
elements can be added in one process that are to be stored as part of the local
matrix in a different process. During the assembly phase the stashed values
are moved to the correct processor. We name it as non-local assembly,
which causes thread safe issues within the momentumt4ht@95xdg assembly
loop.
Luckily, when the parameter MATt4ht@95xIGNOREt4ht@95xOFFt4ht@95xPROCt4ht@95xENTRIES
is set, any MatSetValues accesses to rows that are off-process will be discarded, and
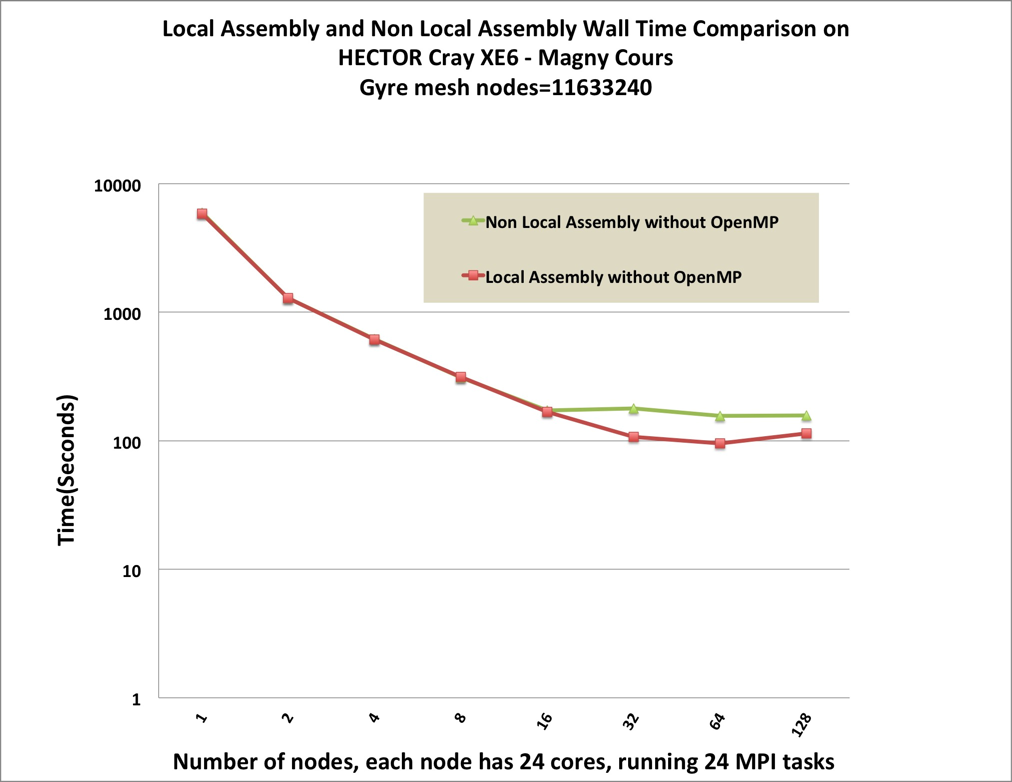
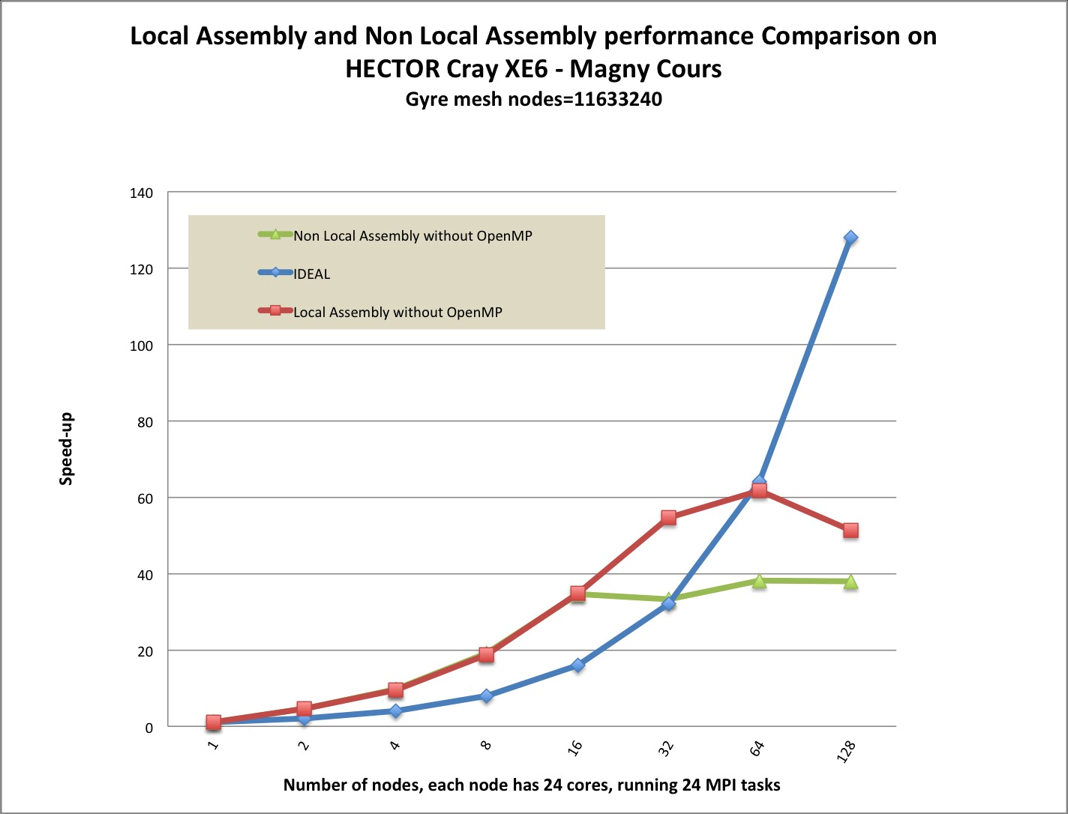
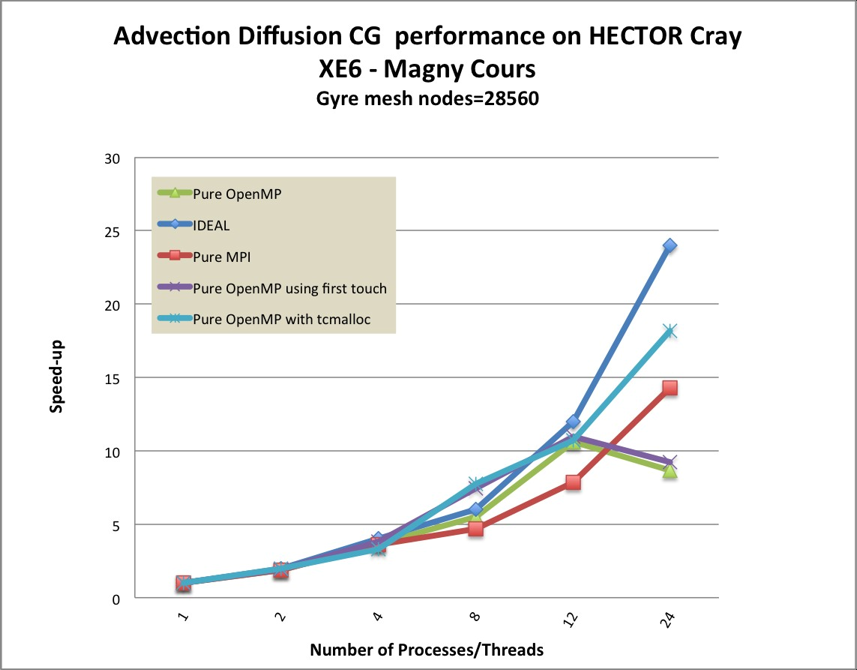
the needed value will be computed locally, namely by local assembly. Figures 1 and
2 show the benchmark results comparing local and non-local assembly
for the oceanic gyre test case which uses DG for momentum and CG for
advection/diffusion. For low core counts the difference is negligible. This
highlights the fact that the redundant calculations are not significantly
impacting performance when local assembly is used. However, at higher core
counts the scaling is significantly better. On 768 cores, the local assembly
code is 40% faster, effectively increasing the scaling regime by a factor of
two.
This makes assembly an inherently local process, therefore we can focus on
optimising local (on the compute node) performance.
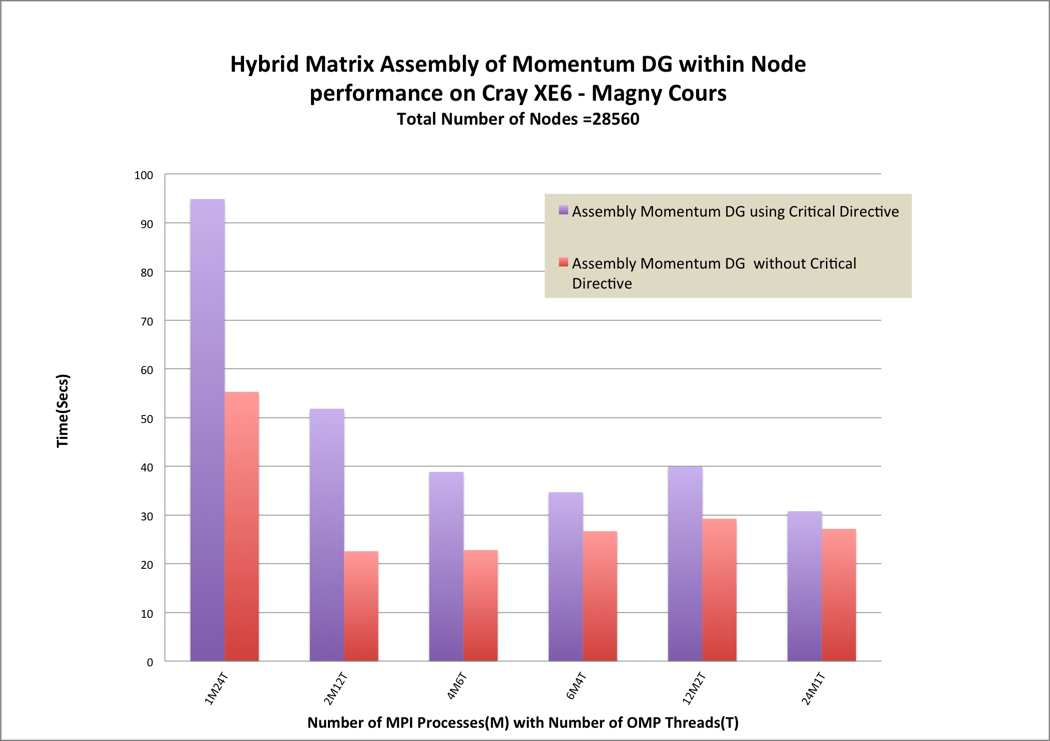
2.4 Thread Safe Issues of Memory Reference Counting
For any defined type objects in Fluidity-ICOM being allocated or deallocated, the
reference count will be plus one or minus one. If the objects counter equals zero,
the objects should then be deallocated. In general, the element-wise physical
quantities should not perform allocation or deallocation in the element loop, but
this is not the case in the kernels. The solution could be to either add critical
directives around reference counter or move allocation or deallocation outside
of element loop. We have implemented both solutions and performance
comparison has been made in Figure 3. We have compared different OpenMP
and MPI combinations within node. Using critical directives, pure MPI
outperformed other combinations. Without using critical directives, the
performance have been improved by more than 50% for 12 and 24 threads.
Therefore, the mutual synchronisation directives (eg. critical) should be
avoided. Moving allocation or deallocation outside of element loop has
also improved the pure MPI versions performance (see 24M1T in Figure
3).
2.5 Optimisation of memory bandwidth
One of the key performance considerations for achieving performance on ccNUMA
nodes is memory bandwidth. In order to optimise memory bandwidth, the following
methods have been employed to ensure good performance:
- First-touch initialisation ensures that page faults are satised by the memory
bank directly connected to the CPU that raises the page fault;
- Thread pinning to ensure that individual threads are bound to the same
core throughout the computation.
Thread pinning has been used through Cray aprun with all benchmark tests. After
applying the first touch policy, compared with the 12-thread runs, the wall time
has been reduced from 45.127 seconds to 38.303 seconds using 12 threads on Cray
XE-Magny Cours. From Figure 5 and Figure 6, the speedup has been improved up
to 12 threads compared between using and without using first touch. But even after
applying the first-touch policy, there is still a sharp performance drop from 12
threads to 24 threads.
| Fig. 4: | CrayPAT Sample Profiling Statistic of Momentumt4ht@95xDG with
24 threads |
Samp% | Samp | Imb. | Imb. |Group
| | Samp | Samp% | Function
| | | | PE=HIDE
100.0% | 75471 | -- | -- |Total
|---------------------------------------------------------------------------
| 95.8% | 72324 | -- | -- |ETC
||--------------------------------------------------------------------------
|| 14.6% | 11002 | 0.00 | 0.0% |_int_malloc
|| 13.8% | 10417 | 0.00 | 0.0% |__lll_unlock_wake_private
|| 9.7% | 7284 | 0.00 | 0.0% |free
|| 9.5% | 7172 | 0.00 | 0.0% |__lll_lock_wait_private
|| 6.4% | 4862 | 0.00 | 0.0% |malloc
|| 6.2% | 4674 | 0.00 | 0.0% |__momentum_dg_MOD_construct_momentum_element_dg
|| 4.0% | 3046 | 0.00 | 0.0% |_int_free
|| 3.2% | 2439 | 0.00 | 0.0% |__momentum_dg_MOD_construct_momentum_interface_dg
|| 3.0% | 2272 | 0.00 | 0.0% |_gfortran_matmul_r8
|| 3.0% | 2251 | 0.00 | 0.0% |__sparse_tools_MOD_block_csr_blocks_addto
|| 2.8% | 2090 | 0.00 | 0.0% |malloc_consolidate
|| 2.1% | 1574 | 0.00 | 0.0% |__fetools_MOD_shape_shape
|
|
This problem has been investigated by profiling with CrayPAT. From Figure 2.5,
we can see the top costs in the Momentumt4ht@95xDG are dominated by memory
allocation. As we have moved all explicit memory allocation outside of element
loop, the culprit appears to be the use of FORTRAN automatic arrays in the
Momentumt4ht@95xDG assembly kernel for support of p-adaptivity. There are a lot
of such arrays in the kernel. Since the compiler can’t predict its length, it allocates
the automatic arrays on the heap.
The heap memory manager must keep trace which parts of memory have been
allocated and which parts of memory are free. In a multi-threaded environment,
this task has been further complicated by multiple threads request to allocate or
deallocate memory from the heap memory manager. In order to keep memory
allocation thread safe, the typical solution to this is to apply the mutual
synchronisation methods, eg: a single lock. In the multiple threads environments,
memory allocation by all threads will be effectively serialised by waiting on the
same lock.
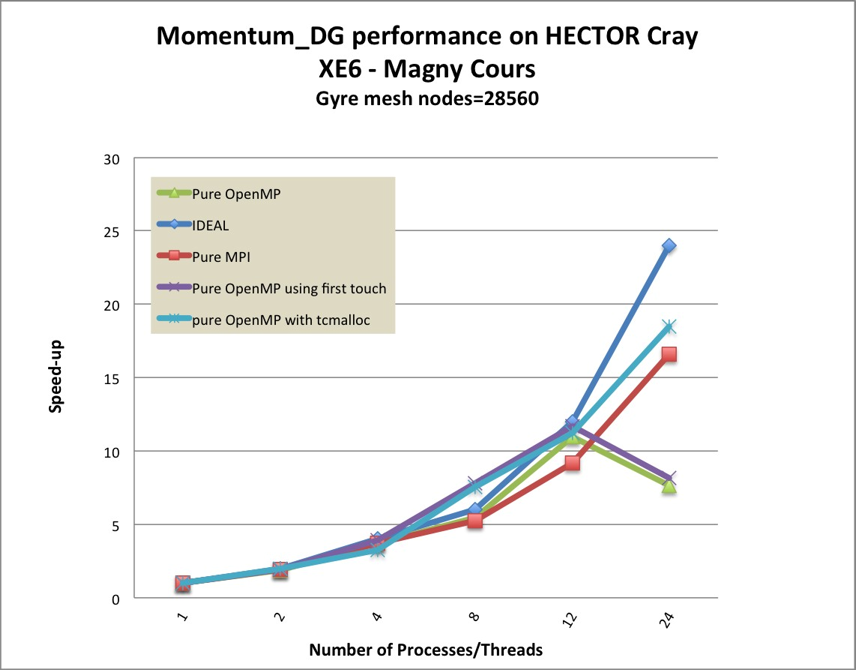
Thread-Caching malloc(TCMalloc)
resolve this problem by using a lock-free approach. It allocates and deallocates
memory (at least in some cases) without using locks for synchronization. This
makes a significant performance boost for pure OpenMP version which is now
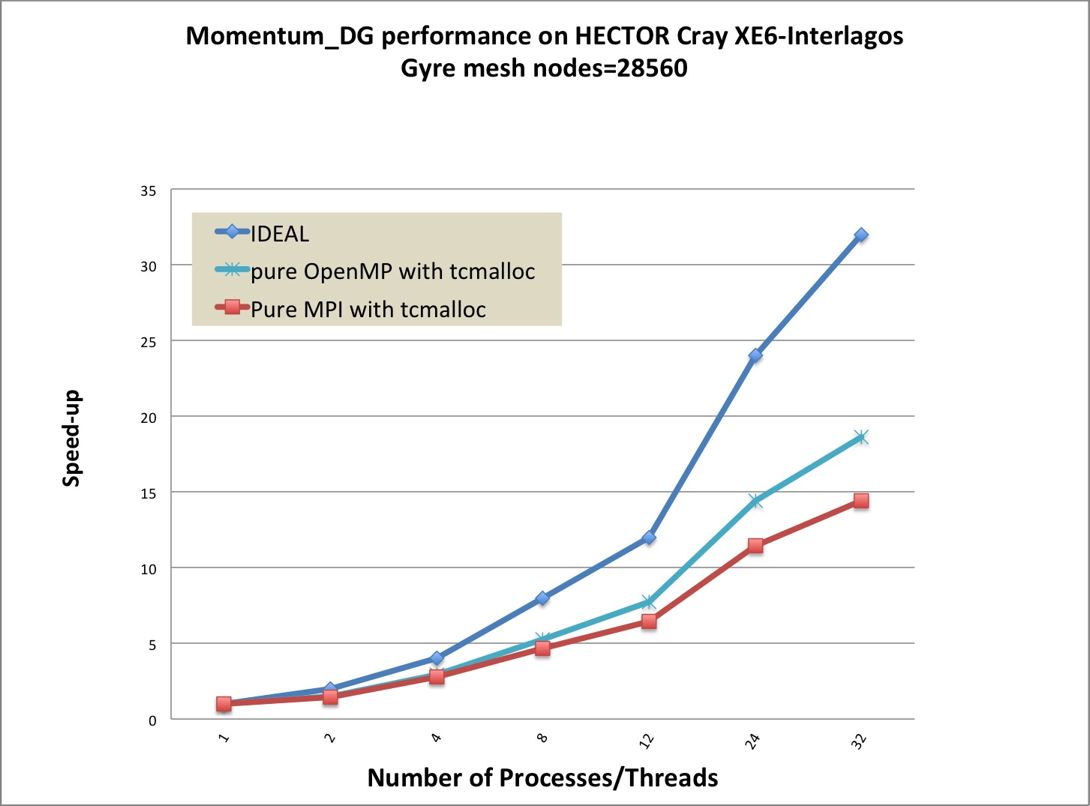
better than pure MPI version within a compute node. Figure 5 shows that
the speedup of 24 threads on Cray XE6-Magny Cours is 18.46 compared
with using 1 thread for the Momentumt4ht@95xDG kernel. On the Cray
XE6-Interlagos(Figure 7), the pure OpenMP still performs better than pure MPI,
though the speed up of 24 threads on Cray XE6-Interlagos drop to 14.42
due to Interlagos’s memory bandwidth being much smaller than Magny
Cours.
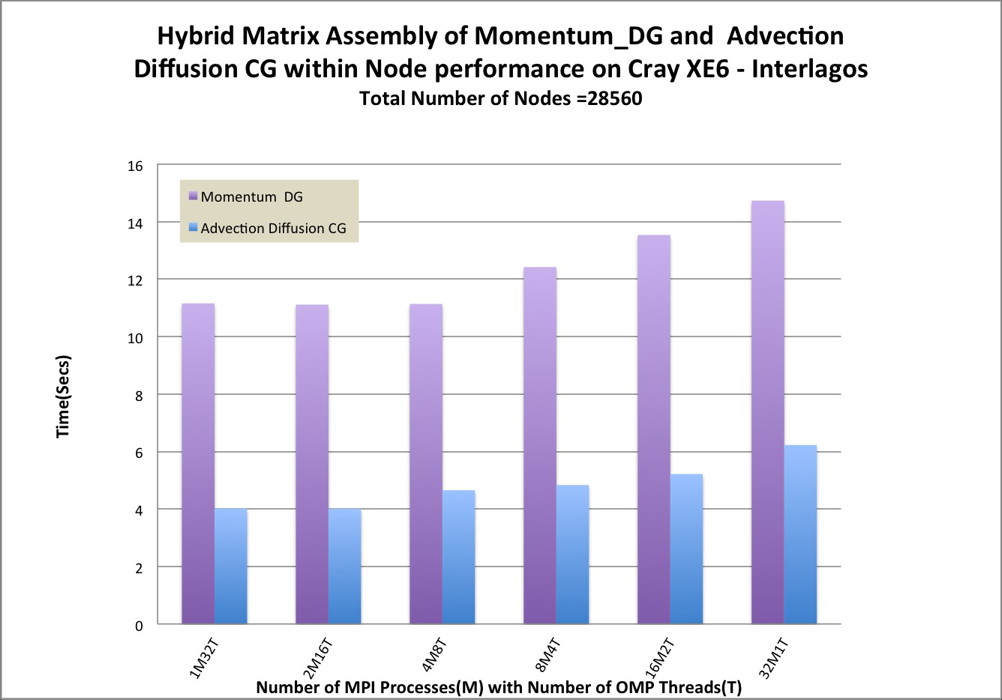
We have also compared the different combination of number of MPI tasks and
OpenMP threads within Cray XE6-Interlagos compute node. From the Figure 8, we
can see that 1 MPI tasks 32 OpenMP threads is competitive with 2 MPI tasks 16
Threads and 4 MPI tasks 8 OpenMP threads.
3 WP2: Optimizing HYPRE Library usage for Linear Preconditioners/Solver for
large core counts
Fluidity-ICOM use PETSc for solving sparse linear systems. Many other scalable
preconditioner/solvers can be called through PETSc interface, eg: HYPRE.
Previous studies (2) have already shown that Fluidity-ICOM spend the majority of
it’s run time in sparse iterative linear solvers. This work-package mainly
investigate BoomerAMG from HYPRE as preconditioner as it has been fully
threaded.
BoomerAMG has two phases: setup and solve. The primary computational kernels
in the setup phase are the selection of the coarse grids, creation of the interpolation
op- erators, and the representation of the ne grid matrix operator on each coarse
grid. The primary computational kernels in the solve phase are a matrix-vector
multiply (MatVec) and the smoothing operator, which may closely resemble a
MatVec.
For most basic matrix and vector operations, such as MatVec and dot product has
been implemented with OpenMP at the loop level. In the setup phase, only the
generation of the coarse grid operator (a triple matrix product) has been threaded.
Both coarsening and interpolation do not contain any OpenMP statements. The
solve phase(MatVec and the smoothing operator) has been completely threaded
(9).
3.1 HYPRE installation on HECToR
We have experimented several versions of HYPRE. Only HYPRE-2.9.1a is working
with Fluidity without crash, which can be downloaded from PETSc website
.
Even with this version, we still need several fixes:
- Hack configure.in to not let HYPRE use it’s own SUPERLU, instead using
SUPERLU from TPSL.
- When linking with Fluidity, make sure not to use libHYPREt4ht@95xgnu
from TPSL.
- The current Fluidity default GNU compiler(gcc 4.6.1) doesn’t work with
HYPRE, replace with gcc 4.6.3
HYPRE BoomerAMG is now a optional preconditioner can be setup with
diamond by Fluidity users, the details can be found in the latest manual
(10).
3.2 PETSc OpenMP branches
We have proposed to do benchmarking and performance analysis of Fluidity with
the new mixed-mode mesh adaptivity library in our original work plan. However,
due to the mesh adaptivity library not being ready for production usage
we changed our plan to benchmarking with PETSc OpenMP branches
instead since the majority of Fluidity-ICOM run time is spent in the sparse
solvers.
PETSc consists of a series of libraries that implement the high-level components
required for linear algebra in separate classes: Index Sets, Vectors and
Matrices; Krylov Subspace Methods and Pre-conditioners; and Non-linear
Solvers and Time Steppers. The Vector and Matrix classes represent the
lowest level of abstraction and are the core building blocks of most of the
functionalities.
In the PETSc OpenMP branches, the Vector and Matrix class are threaded. The
Krylov subspace methods and the pre-conditioners are implemented in the KSP
and PC classes. They have not been threaded explicitly since the basic algorithms,
like CG and GMRES and SOR preconditioners, are based on functionality from the
Mat and Vec classes, which have been threaded. Other frequently used
preconditioners, such as Symmetric Over-Relaxation (SOR) or Incomplete
LU-decomposition (ILU), have not been threaded yet due to their complex data
dependencies. These may require a redesign of the algorithms to improve parallel
efficiency (11).
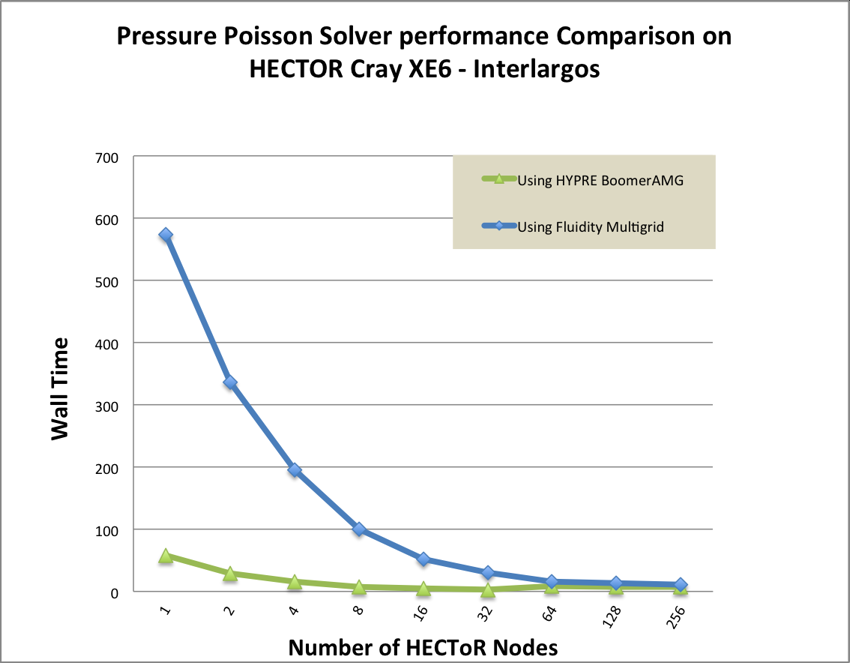
We have compared BoomerAMG preconditioner with Fluidity’s own Multigrid
preconditioner for the pressure Poisson solver of the lock exchange test case. Figure
9 shows that BoomerAMG outperforms Fluidity’s own multigrid precondioner.
Therefore, in the final benchmarking we always use BoomerAMG for Pressure
Poisson solver. But for those problems in which there is a large variety in length
scales, Fluidity’s own Multigrid may still be the only choice. Further investigations
are required here.
3.3 WP3: Final Benchmarking and Performance Analysis
The lock exchange test case has been used here. The lock exchange is classic CFD
test problem. A lock separates two fluids of different densities (e.g. hot and cold)
inside a tank; when the lock is removed, two gravity currents propagate along the
tank. An 3.4 million vertices mesh, resulting in 82 million degrees of freedom for
velocity, has been used for the scalability analysis on large number of cores.
The benchmark starts with 2 HECToR Interlargos nodes and scales up to
1024 nodes (32768 cores). The speedup are obtained with the following
formula:
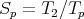 | (1) |
Where T2 is the wall time with 2 nodes, each node comprises 32 AMD Interlagos
cores, Tp is the wall time with p nodes(P ≥ 2).
Figure 10 shows that matrix assembly scales well up to 32K cores. The speedup of
mixed mode is 107.1 compare with 99.3 of pure MPI by using 256 nodes. This id
due to the use of local assembly which make this part of the code essentially a local
process. Hybrid mode performs slightly better than pure MPI, which can scale well
up to 32K cores.
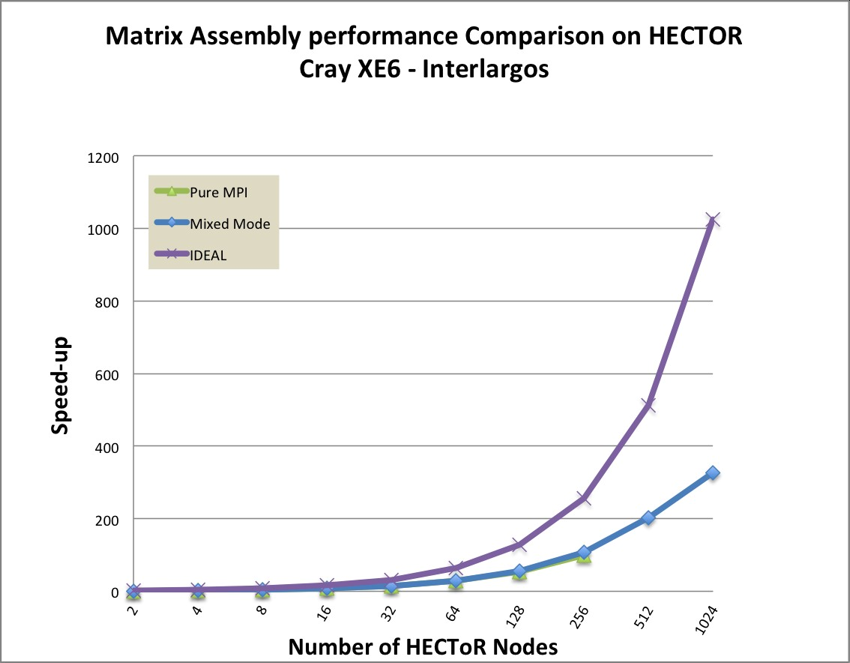
Figure 11 describes speedup of solving pressure Poisson equation using
preconditioner HYPRE BoomerAMG and solver Conjugate gradient. It
indicates that pure MPI performance starts to degrade from 64 HECoR nodes
(2048 cores) onwards where the hybrid mode begin to outperform pure
MPI.
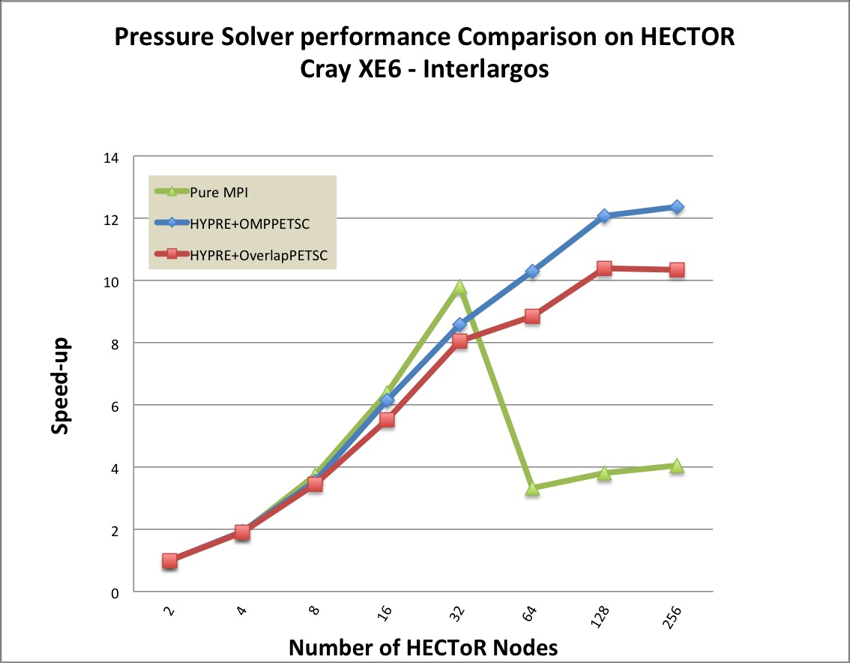
Figure 12 shows the speedup of solving momentum equation using DG with
preconditioner HYPRE BoomerAMG and solver GMRES. The performance of
mixed mode are comparable with pure MPI version, but pure MPI performs better
than mixed mode for up to 8K cores. This is due to number of degree of freedom
for velocity are 24 times bigger than pressure, there are enough work for up to 8K
cores. The PETSc task based OpenMP(12) branch performs better than vector
based OpenMP(11) branch.
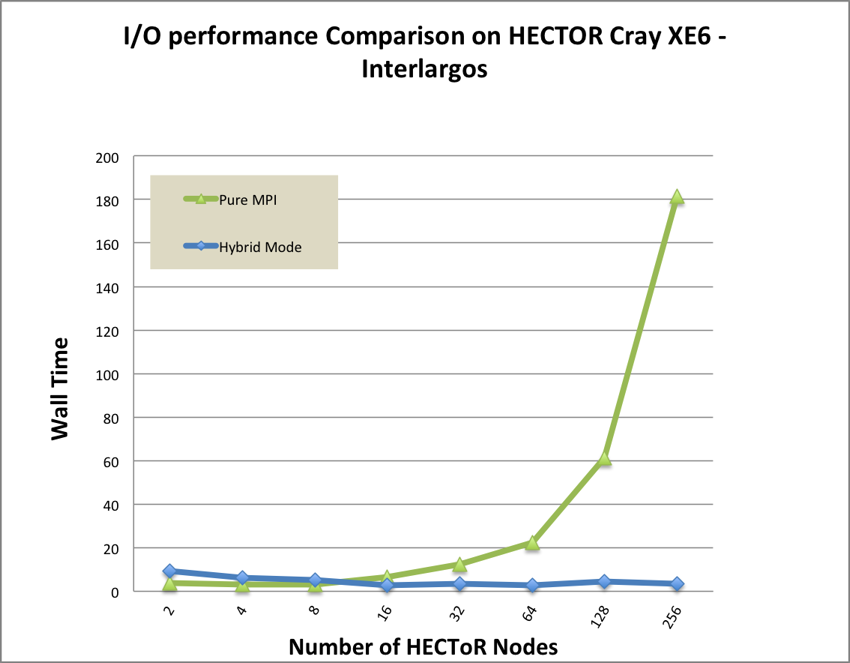
We have switched off all writes, so the only I/O is reading input including flml file
and mesh files. From Figure 13, we can see that significant I/O efficiency has been
achieved by using mixed mode parallelism. For example, only four process per node
will be involved in I/O (with pure MPI potentially 32 processes per node are
performing I/O under current Phase 3 of HECToR), which reduces the number of
metadata operations on large numbers of nodes, which may otherwise hinder
overall performance. In addition, the total size of the mesh halo increases with
number of partitions (i.e. number of processes). For example, it can be shown
empirically that the size of the vertex halo in a linear tetrahedra mesh
grows proportionally as O(Pexp(1.5)), where P is the number of partitions.
Therefore, the use of hybrid OpenMP/MPI will decrease the total memory
footprint per compute node, the total volume of data to write to disk, and the
total number of metadata operations based on the files-per-process I/O
strategy.
4 Summary and Conclusions
We have focused on Fluidity-ICOM matrix assembly. Above performance results
indicate that node optimisation can be done mostly using OpenMP with efficient
colouring method, which avoids the use of mutual synchronization directives: eg.
Critical. Regarding Matrix stashing, it does not have any redundant calculations.
However, it does incur the cost of maintaining and communicating stashed rows,
and this overhead will increase for higher MPI process counts. A further
complication of non-local assembly is that the stashing code within PETSc is not
thread safe.
Local assembly has the advantage of not requiring any MPI communications as
everything is performed locally, and the benchmark results also highlights the fact
that the redundant calculations are not significantly impacting performance when
local assembly is used. Furthermore, the scaling of local assembly is significantly
better than non-local assembly at higher core counts. This makes assembly an
inherently local process. Thus focus is on optimizing local (to the compute node)
performance. The matrix assembly kernels can scale well up to 32K core counts
with mixed mode.
As the current OpenMP standard (3.0), which has been implemented by most
popular compilers, doesn’t cover page placement at all, memory-bound
applications, like Fluidity-ICOM, require explicit memory placement. Hereby it is
important to make sure that memory get’s mapped into the locality domains of
processors that actually accesses the data. This was achieved by implementing a
first touch policy to minimize NUMA traffic across the network. Using thread
pinning was then used to guarantee that threads are bound to physical CPUs and
maintain locality of data access.
For Fluidity-ICOM matrix assembly kernels, the performance bottle neck
becomes memory allocation for automatic arrays. Using NUMA aware heap
managers TCMalloc, it makes pure OpenMP version outperform the pure MPI
version.
For high core counts simulation, the I/O becomes major bottleneck for pure MPI
version. Significant efficiency of I/O based on files-per-process strategy has been
achieved by using mixed mode parallelism.
5 Future work
During benchmarking, we found one of many difficulties coming from decomposing
mesh for high core counts. Though mixed mode have reduce quite large mount of
time by reducing number of partitions. But even with 4K partitions, the
decomposition of a medium sized mesh are still requiring few hours to finish. This
majority time of fldecomp are spent in construction halos for each partitions. A
parallel halo constructor are required here.
We will spend more efforts on solvers, we will further investigate threading
preconditioner that can be called through PETsc. We currently have the access to
the ongoing project about hybridize PETSc with OpenMP. This work offers
potential capabilities to further increase parallel performance of Fluidity-ICOM
with mixed mode MPI/OpenMP.
After this, we will investigate the fully OpenMP parallelized Fluidity-ICOM on
Intel MIC and Cray XK6, which will further guide us the future development.
When the Parallel anisotRopic Adaptive Mesh
ToolkIt
is ready for production usage, we will benchmark and optimize this threaded
adaptive mesh library together with fluidity
Acknowledgements
The authors would like to acknowledge the support of a HECToR distributed
Computational Science and Engineering award. The authors would also like to
thank the HECToR/NAG support team for their help throughout this work. The
author would also thanks Dr. Lawrence Mitchell and Dr. Michele Weiland for their
valuable contributions. The author would also like to thank his colleagues, Dr.
Stephen Pickles, Dr. Andrew Porter, for their valuable suggestions and
discussions.
This project was funded under the HECToR Distributed Computational Science and Engineering (CSE)
Service operated by NAG Ltd. HECToR - A Research Councils UK High End Computing Service - is the UK's
national supercomputing service, managed by EPSRC on behalf of the participating Research Councils.
Its mission is to support capability science and engineering in UK academia. The HECToR supercomputers
are managed by UoE HPCx Ltd and the CSE Support Service is provided by NAG Ltd. http://www.hector.ac.uk
References
[1] Xiaohu Guo, G. Gorman, M Ashworth, A. Sunderland,
Developing hybrid OpenMP/MPI parallelism for Fluidity-ICOM - next
generation geophysical fluid modelling technology, Cray User Group
2012: Greengineering the Future (CUG2012), Stuttgart, Germany, 29th
April-3rd May 2012
[2] Xiaohu Guo, G. Gorman, M Ashworth, S. Kramer, M. Piggott, A.
Sunderland, High performance computing driven software development for
next-generation modelling of the Worlds oceans, Cray User Group 2010:
Simulation Comes of Age (CUG2010), Edingburgh, UK, 24th-27th May
2010
[3] Welsh, D. J. A.; Powell, M. B., An upper bound for the chromatic
number of a graph and its application to timetabling problems, The
Computer Journal, 10(1):8586, 1967 doi:10.1093/comjnl/10.1.85
[4] P. Berger, P. Brouaye, J.C. Syre, A mesh coloring method for
efficient MIMD processing in finite element problems, in: Proceedings of the
International Conference on Parallel Processing, ICPP’82, August 24-27,
1982, Bellaire, Michigan, USA, IEEE Computer Society, 1982, pp. 41-46.
[5] T.J.R. Hughes, R.M. Ferencz, J.O. Hallquist, Large-scale vectorized
implicit calculations in solid mechanics on a Cray X-MP/48 utilizing EBE
preconditioned conjugate gradients, Comput. Methods Appl. Mech. Engrg.
61(2), (1987a), 215-248.
[6] C. Farhat, L. Crivelli, A general approach to nonlinear finite-element
computations on shared-memory multiprocessors, Comput. Methods Appl.
Mech. Engry. 72(2), (1989), 153-171.
[7] D. Komatitsch, D. Michaa, G. Erlebacher, Porting a high-order
finite-element earthquake modeling application to NVIDIA graphics cards
using CUDA, J. Parallel Distrib. Comput. 69, (2009), 451-460.
[8] C. Cecka, A.J. Lew, and E. Darve, Assembly of Finite Element
Methods on Graphics Processors, Int. J. Numer. Meth. Engng 2000, 1-6.
[9] A.H. Baker, M. Schulz and U. M. Yang, On the Performance of
an Algebraic Multigrid Solver on Multicore Clusters, in VECPAR 2010,
J.M.L.M. Palma et al., eds., vol. 6449 of Lecture Notes in Computer
Science, Springer-Verlag (2011), pp. 102-115
[10] Fluidity
Manual. Applied Modelling and Computation Group, Department of Earth
Science and Engineering, South Kensington Campus, Imperial College
London, London, SW7 2AZ, UK, version 4.1 edn. (May 2012), available at
https://launchpadlibrarian.net/99636503/fluidity-manual-4.1.9.pdf
[11] M. Weiland, L. Mitchell, G. Gorman, S. Kramer, M. Parsons, and J.
Southern, Mixed-mode implementation of PETSc for scalable linear algebra
on multi-core processors, In Proceedings of CoRR. 2012.
[12] Michael Lange, Gerard Gorman, Michele Weiland, Lawrence
Mitchell, James Southern, Achieving efficient strong scaling with PETSc
using Hybrid MPI/OpenMP optimisation, submitted to ISC’13, 2013
 independentt4ht@95xelements do
independentt4ht@95xelements do