Mesh reordering in Fluidity using Hilbert space-filling curves
Mark Filipiak
EPCC, University of
Edinburgh
March 2013
Abstract
Fluidity is open-source, multi-scale, general purpose CFD model. It is a finite element model using an unstructured mesh which is adapted during the course of a simulation. Reordering of the mesh elements and vertices has been implemented, reordering occurring at input and at each adapt step. For an OpenMP simulation using all 4 UMA regions in a single HECToR node, a 3‒5% performance improvement is seen overall, with a 5‒20% improvement in the threaded element assembly and solve steps.
Fluidity is an open-source, multi-scale, general purpose CFD model developed by the Applied Modelling and Computation Group (AMCG) at Imperial College. The focus for development of Fluidity is ocean modelling. Fluidity is capable of resolving flows simultaneously on global, basin, regional, and process scales, enabling oceanographic research that is not possible with other models. It is an adaptive model that can optimise the number and placement of computational degrees of freedom dynamically through the course of a simulation. The long term aim is the capability to simulate the global circulation and to resolve selected coupled dynamics down to a resolution of 1km – in particular, ocean boundary currents, convection plumes, and tidal fronts on the NW European shelf.
Fluidity currently runs on a range of computing platforms, from desktop workstations to HPC platforms, such as HECToR. Fluidity is currently limited for the size of problems that are being investigated, especially on systems with NUMA (Non Uniform Memory Access) multicore processors, of which HECToR is an example. The purpose of this project is to improve the scaling behaviour of Fluidity by implementing memory access techniques to better exploit the hybrid OpenMP/MPI code within the finite element assembly and solve routines.
The key objective of this project was to improve the ordering of topological and computational meshes in Fluidity, by adding new features in Fluidity's decomposition software, fldecomp, and adding mesh renumbering code in the central Fluidity trunk code. Correct functionality would be checked with new tests added to the existing suite of 22,000 unit and regression tests. NUMA performance would be profiled and benchmarked.
A subsidiary objective was to improve the colouring strategy used in the hybrid assembly loops to allow non-dependent element assembly to be performed concurrently. The existing strategy adversely affects cache coherency.
The work to add the mesh renumbering code in the central Fluidity trunk code was technically challenging and took much longer than planned in the proposal. This meant that the scope of the key objective was reduced and the subsidiary objective was not achieved. Only Hilbert space-filling curve renumbering was implemented; other methods can be readily added to the code. The renumbering is so central in the code that the existing regression tests were sufficient to test correct functionality. The renumbering is applied to the topographical mesh only. Discontinuous Galerkin and higher order elements are created at run time and the quality of their numbering is strongly dependent on the quality of the numbering of the topographical mesh. So that we can access the benefit of renumbering directly, we focus on the backward facing step test case, which uses a first-order, piecewise linear, continuous Galerkin discretisation
The “first touch” memory policy is implemented in Fluidity to ensure memory pages are bound to local memory on NUMA architectures (e.g. the array of velocities at the nodes of the computational mesh). It is assumed that thread/process affinity is specified in the user environment (aprun enforces this on HECToR for example). However, this does not translate into locality of memory access during the assemble step if the data for the physical nodes comprising an element are not located close to each other in memory, nor, during the solve step, if the physical neighbours of a node are not located close to each other in memory.
In general, mesh construction methods are designed to produce correct meshes rather than meshes with good data locality. Even if the mesh generator renumbers the mesh before outputting, subsequent domain decomposition for MPI can degrade data locality. Reordering the mesh in the Fluidity data structures can improve the data locality so that during assembly, the data for each element is all close in memory and, during solution, the node-to-node memory distance is small, reducing matrix band widths.
Many methods have been used for choosing a good ordering of
nodes in a computational mesh (e.g. nested dissection, quadtree/octree
decomposition, space-filling curves) or
in the resulting matrix to be solved (e.g. reverse Cuthill-McKee ordering)
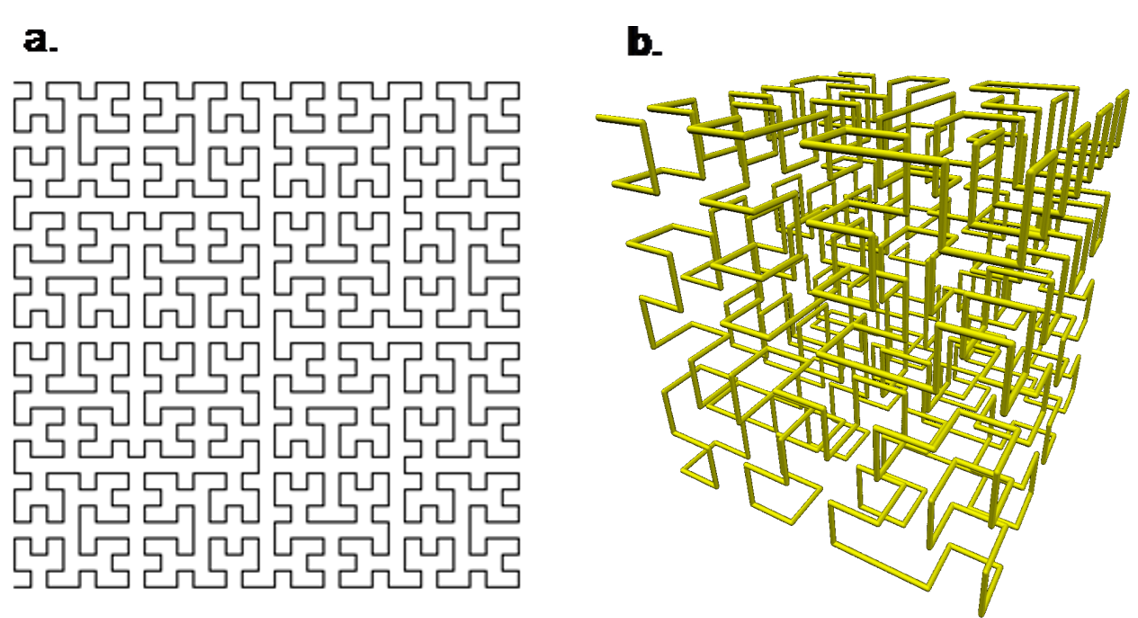
Figure 1: a. 5th order Hilbert curve in 2D [from en.wikipedia.org, author António Miguel de Campos]. b. 3rd order Hilbert curve in 3D [from hr.wikipedia.org, author Stevo-88].
The traversal of the hierarchical structure of the dissection or of the curve gives the desired locality of nodes in the ordering. Nodes that are close in the ordering will be close in the mesh or in the physical domain. However, there will be ‘boundary’ nodes at all scales which are close in the mesh or physical domain but which are far apart in the ordering; this cannot be avoided. Both methods have a hierarchical structure in physical space, so that there is locality at all scales. The locality property is just what is needed for ensuring physical locality corresponds to memory locality. The hierarchical property means that the methods can be generally applied without tuning to the actual number of UMA regions. The hierarchical structure also means that the resulting ordering will also have good cache locality, no matter what size or number of levels of cache.
The two methods have their advantages and disadvantages:
Nested dissection
Advantages
· Mesh-based, so will work with any topology, e.g. thin spherical shells (oceans).
Disadvantages
· Choice of sub-mesh size at which to stop the recursion will depend on the cache size of the processor but usually be much smaller than the size of a UMA region so will still be ‘NUMA-oblivious’.
· May be slow to calculate the bisections.
Hilbert space-filling curve
Advantages
· Assuming the machine precision is large enough to generate a high order approximation to the Hilbert curve, locality will be achieved at all scales, so the ordering will be cache-oblivious and NUMA oblivious.
· Can be fast to calculate the ordering.
Disadvantages
·
Ordering is based on the physical coordinates
and may give poor results for physical domains with extreme aspect ratios or
that are embedded in a higher dimension space, e.g. spherical shells
(oceans). Recent work on mesh traversal
by a self-avoiding walk
Because of the modularity of the task, and its wide application, renumbering methods have been implemented in many high performance software libraries. In Table 1 we list the libraries considered.
Table 1: Possible software libraries for renumbering
|
Library |
Open source |
Parallel |
Comments |
|
Boost graph library |
yes |
yes |
Several sparse matrix ordering schemes (only in the serial library). |
|
Leda |
no |
no |
No ordering or decomposition algorithms. |
|
Scotch |
yes |
yes |
Recursive dissection ordering. Scotch is included in Zoltan. |
|
Zoltan |
yes |
yes |
Contains Scotch and ParMetis, and Hilbert space-filling curve ordering. |
|
Chaco |
yes |
no |
Partitioning only. |
|
Jostle |
no |
evaluation version only |
Partitioning only. |
|
ParMetis |
yes |
yes |
Recursive dissection ordering. ParMetis is included in Zoltan. |
Zoltan is already integrated into the Fluidity code for load
balancing and Zoltan provides Hilbert space-filling curve ordering and recursive
dissection ordering (via its 3rd party libraries ParMetis and
Scotch). Thus Zoltan was the obvious
choice of library to use. During the
project there was time only to evaluate the Hilbert space-filling curve
method. However, the literature
indicates that this is a particularly good choice cache-oblivious choice for
unstructured computation
The main computation in Fluidity consists of the assembly and solution of the momentum (velocity), pressure, and transport equations. The velocity, pressure and tracer fields are defined on the same elements as the basic mesh but can have different order (e.g. quadratic elements) and different continuity. The meshes for these fields are derived from the basic mesh and will have the same elements and element connectivity but can have different numbers of nodes and node connectivity and require ordering separately. Colleagues at Imperial College, London are developing a numbering scheme for such derived meshes but this still requires that the basic mesh has a good ordering to start with.
In Fluidity, data structures are hierarchical, with a “state” variable holding the current simulation state. This state variable holds multiple fields, each of which carry information about the discretisation they are using, which in turn carries information on the topological mesh. In addition, any decomposition must also work with extruded and periodic meshes. Extruded meshes are commonly used in oceanic simulations, where a 2-D surface mesh is created and then extruded downwards to a known bathymetry to create either a z-layered or σ-layered mesh. As such, only the 2-D mesh is decomposed, but the full 3-D mesh must still be ordered correctly. Periodic meshes contain connectivity between elements on one or more of the domain edges, which must be taken into account when ordering elements.
An initial step was to convert the code to use the Fluidity-based tool flredecomp instead of the stand-alone tool fldecomp for the initial decomposition of a mesh when running in parallel. Then the reordering code could be added to Fluidity only. The regression tests were converted to use flredecomp and some bugs uncovered by this change were corrected.
The positions of the mesh vertices and element centres are re-ordered together so that the element ordering matches the node ordering. This gives a permutation to be applied to the meshes and positions (and auxiliary data structures). These reordered meshes are used as normal in Fluidity to derive all the other meshes on which the fields are defined.
There are three cases where the topological mesh should be renumbered:
· when the initial mesh is input, unless some input data (e.g., from a checkpoint) is defined on the initial mesh;
· after the mesh is adapted: this is the easiest case and the new mesh can always be re-ordered since all the fields are interpolated from the old meshes to the new meshes.
· in the middle of load balancing, after the basic mesh has been load balanced but before the fields have been re-distributed across the processors. In this case, the mapping from ‘universal’ (over all MPI processes) numbers to ‘global’ (local to one MPI process) numbers also has to be permuted.
The mesh in each process is reordered separately, within each process. This is sufficient to improve the NUMA and cache performance but does mean that the halo regions, shared between processes, cannot be reordered: Fluidity exploits a fixed order in the haloes to overlap communications and computation.
The code is now available as a branch of the Fluidity code (https://code.launchpad.net/~fluidity-core/fluidity/hilbert) and is currently being reviewed for merging into the main development trunk. It will be made generally available at the first available release of Fluidity.
The code was developed on a local machine that is the equivalent of 2 nodes of HECToR Phase 2. The regression tests were also performed on this machine. Using reordering is sometimes faster and sometimes slower for these tests. Over the 50 largest tests, assembly using the reordered meshes took 95-105% of the time for the unordered meshes, depending on the test. The velocity solve using the reordered meshes takes 90-120% of the time for the unordered meshes, depending on the test. However, these tests are all much smaller than real-world simulations, and in many cases the input mesh already has a good ordering. Example meshes, original and reordered, are shown in Figure 2, Figure 3, and Figure 4. The re-ordering of the mesh in each process does not affect the halo regions shared between processes, as shown in Figure 5.
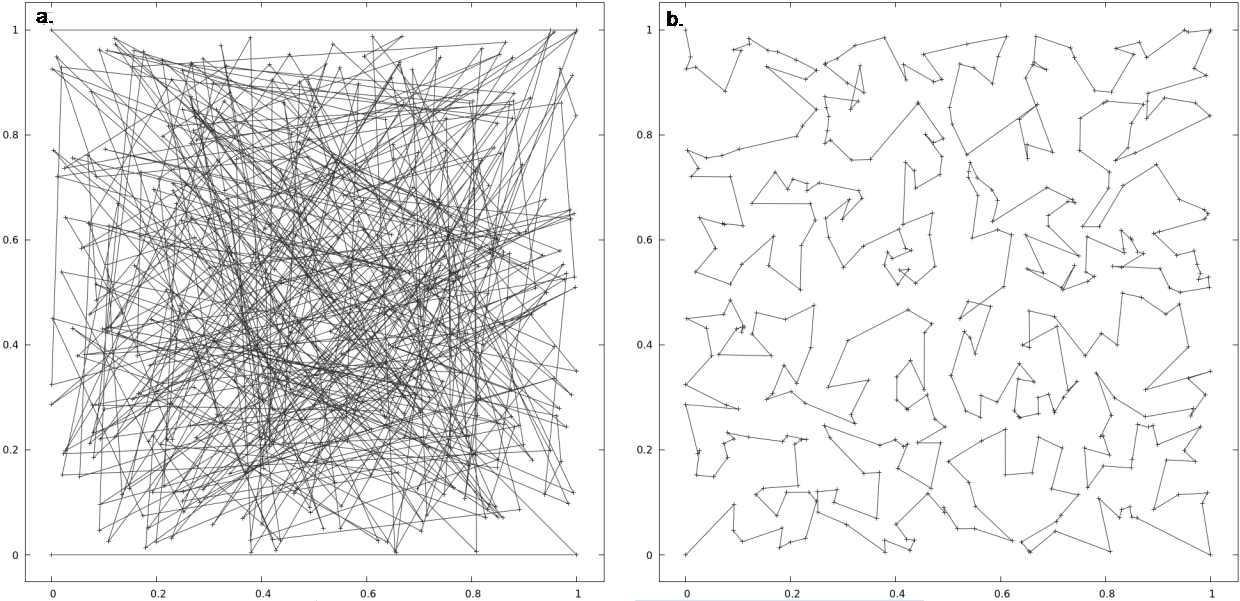
Figure 2: Mesh for 2D tracer diffusion (test case prescribed_adaptivity): a. Original ordering of the coordinate mesh nodes. b. Hilbert ordering of the coordinate mesh nodes.
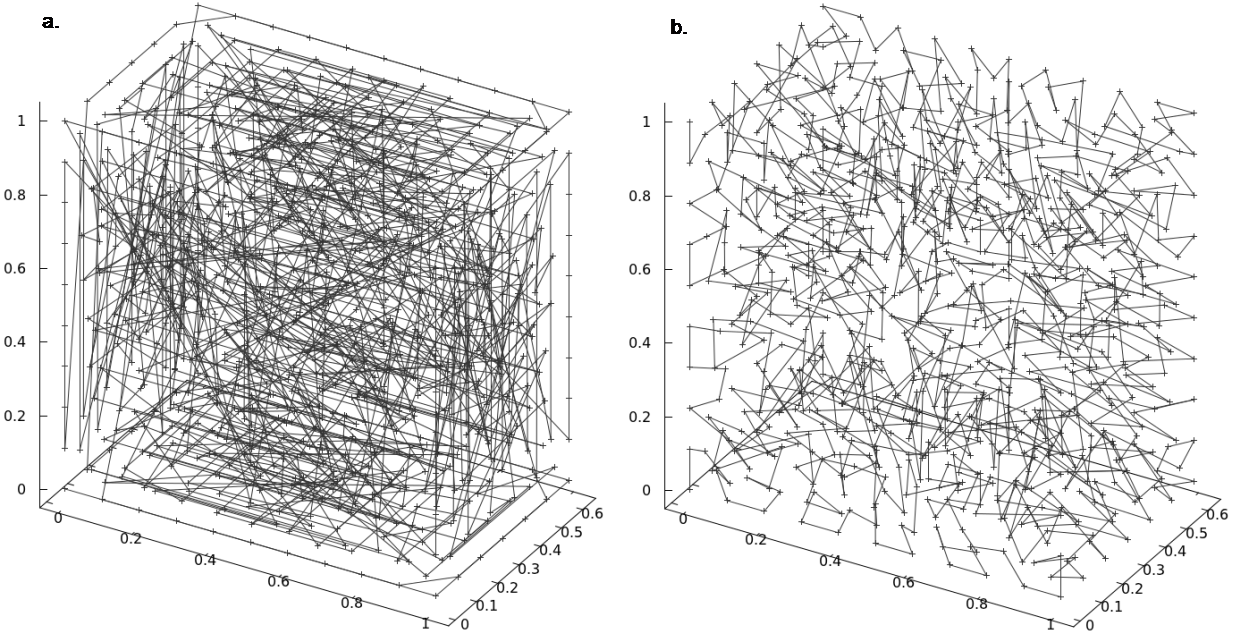
Figure 3: Mesh for a 3D Stokes flow (test case Stokes_3d_busse_1a_p2p1): a. Original ordering of the coordinate mesh nodes. b. Hilbert ordering of the coordinate mesh nodes.
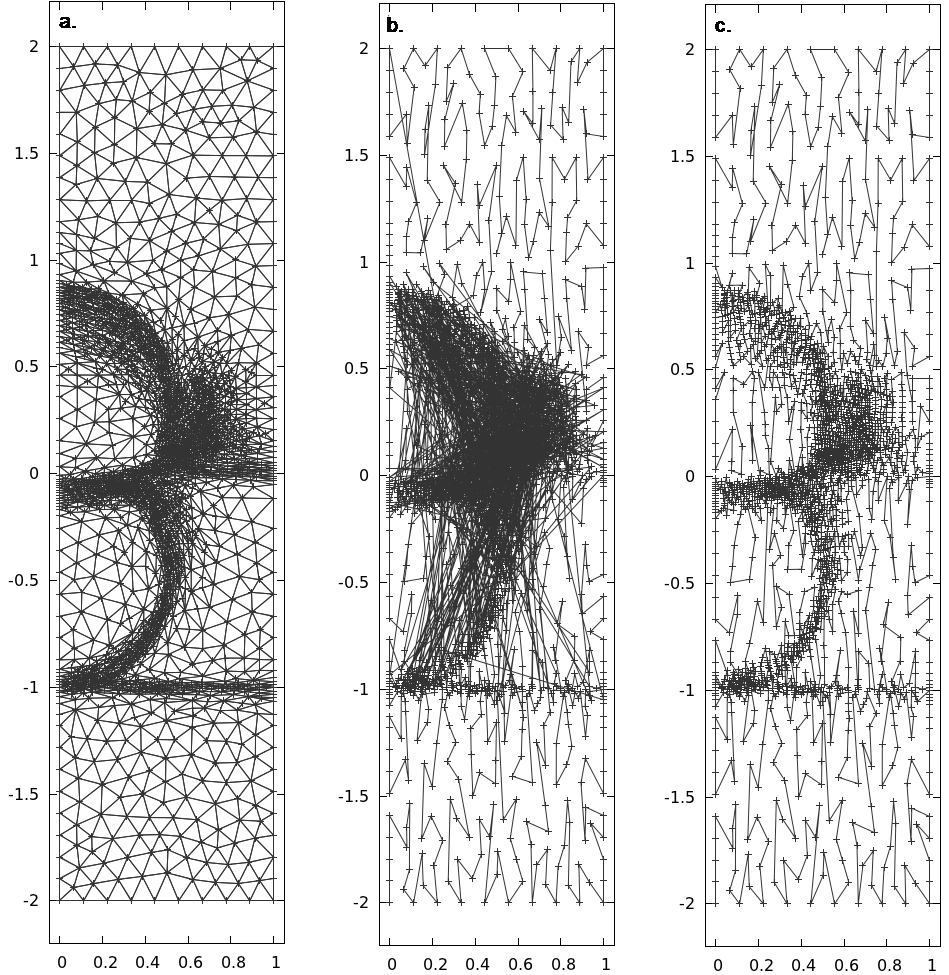
Figure 4:Mesh for a 2D simulation of droplets colliding at an air-water interface (test case 5material-droplet-adapt): a. Mesh after several mesh adaptation steps. b. Ordering just after the last adaptation: the poorly ordered nodes are for elements that have been adapted. c. The reordering after the adaptation restores a good ordering for all nodes.
One measure of the improvement in memory locality for the solve step is the distribution of differences in array index (equivalent to distance in memory) of neighbouring nodes. This distribution is shown in Figure 6 for the cases used for Figure 2, Figure 3, and Figure 4. The node-distance distribution shifts to smaller distances when the mesh is re-ordered.
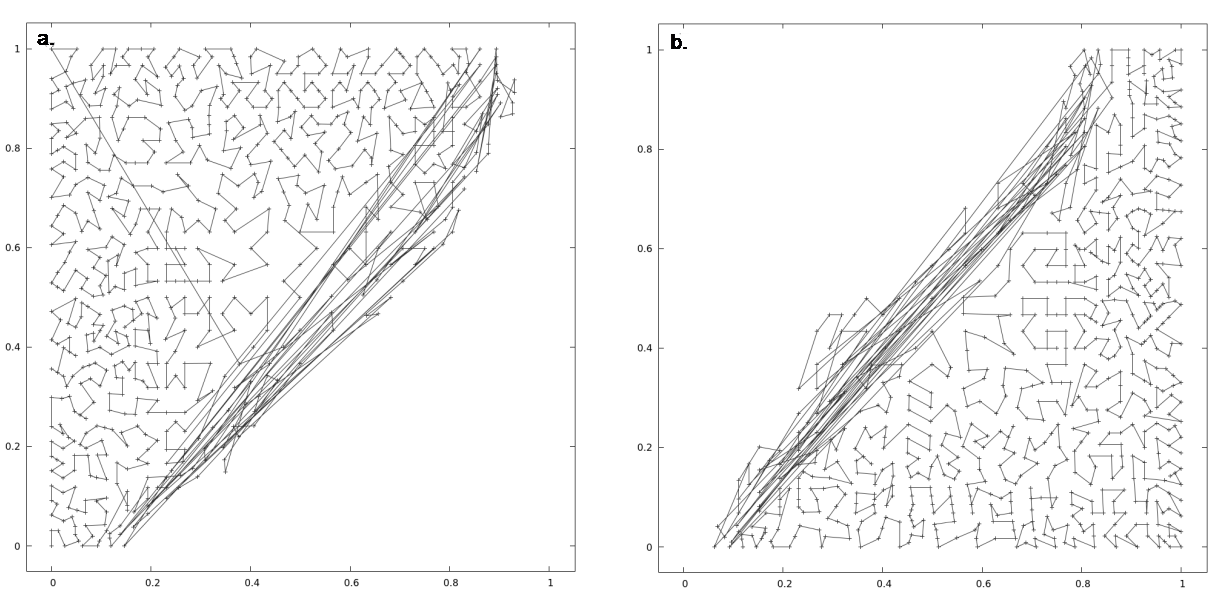
Figure 5: Mesh for 2D convection, run on 2 MPI processes (test case square-convection-parallel): a. Hilbert ordering on process 0. b. Hilbert ordering on process 1. The halo nodes communicated between the processes are not reordered since they are stored at the end of the node array in memory for improved communication.
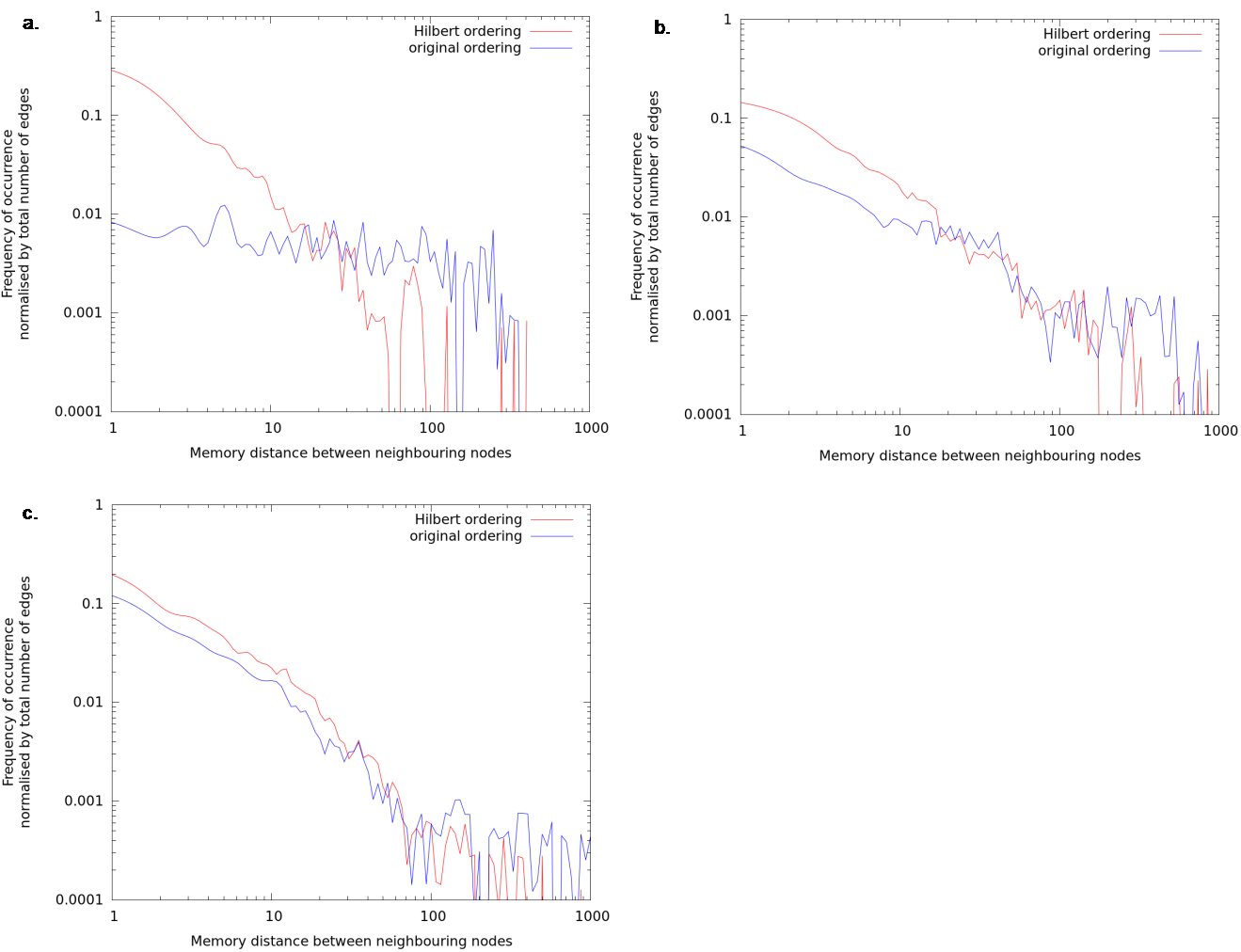
Figure 6: Frequency distribution of memory distance of neighbouring nodes: a. 2D tracer diffusion (test case prescribed_adaptivity). b. 3D Stokes flow (test case Stokes_3d_busse_1a_p2p1). c. 2D simulation of droplets colliding at an air-water interface (test case 5material-droplet-adapt).
Benchmark test
A larger example, representative of the laboratory/industrial
flows that are solved by Fluidity, is the direct numerical simulation of the
flow over a backward-facing step
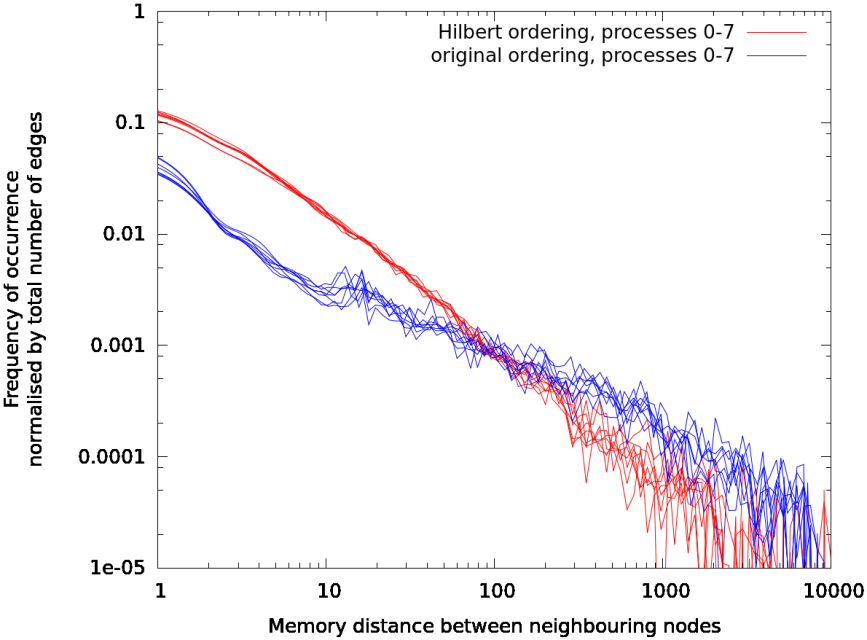
Figure 7: 3D backward-facing step flow (test
case backward_facing_step_3d) at
simulation time = 0.2 (usually the simulation runs to simulation time = 75),
comparing the meshes of a run without any reordering with a run with Hilbert
reordering (i.e. this is not mesh ‘before and after’ a reorder but meshes at
the same simulation time for completely separate runs). Simulation size is ~30,000 nodes. MPI only run, with 8 MPI processes on a
single HECToR node.
MPI
Although the main interest is in the OpenMP and hybrid performance, initial single-node runs of the backward-facing step simulation on HECToR were made using MPI only. The simulation was modified to remove all intermediate I/O to reduce the effect of I/O on the overall wall-clock times. The speed-up due to reordering depended on the number of MPI processes. With 2 processes, the speed-up is 5% overall (wall-clock time, including the time for reordering and for I/O), 10% for the pressure calculation (assemble, setup, and solve), and 7% for the velocity calculation. For this simulation, most of the time is spent in the velocity assembly and the mesh adapt: other simulations may have a different balance between assembly, solve and adapt. For larger numbers of processes, reordering did not give an overall speed-up and could result in slower execution (5% slower overall when using 16 processes); it is not clear why there is not a consistent speed up for all numbers of processes.
OpenMP
To estimate the performance of a hybrid code, the simulation size was increased and the simulation was run on one HECToR node as a single MPI process containing various numbers of OpenMP threads. This is analogous to one MPI process of a hybrid code with one MPI process per node. The difference is that there will be no haloes, which should be a small fraction of the total mesh for large simulations.
The simulation size was increased from ~30,000 to ~1,000,000 nodes (which takes ~4GB memory: a HECToR node has 32GB memory) by modifying the adapt parameters and running for a few adapt steps. The simulation was run again using this larger mesh size and the simulation stopped after 20 time-steps plus the adapt step. This gives enough data, in a reasonable time, to compare the speeds for unordered and reordered meshes.
The thread placement was chosen to accentuate NUMA effects. A HECToR node has 32 cores distributed over 4 UMA regions (0, 1, 2, 3). The HyperTransport links between UMA regions 1 and 2 and between regions 0 and 3 have the lowest bandwidth so the threads were arranged as shown in Table 2.
Table 2: Distribution of threads over
UMA regions to accentuate NUMA effects
|
Number of threads |
UMA region |
|||
|
0 |
1 |
2 |
3 |
|
|
1 |
|
0 |
|
|
|
2 |
|
0 |
1 |
|
|
4 |
0 |
1 |
2 |
3 |
|
8 |
0, 1 |
2, 3 |
4, 5 |
6, 7 |
In theory, this arrangement should show the largest effect of reordering when 2 threads are used together with first-touch initialisation. However the results (Figure 8) show that with 2 threads, using a reordered mesh rather than the unordered mesh actually slows down the simulation. The unthreaded parts of the code (running in UMA region 1) will have slower access to the first-touch-distributed memory in UMA region 2 but, in theory, reordering should not make this any slower.
The results for 1, 4 and 8 threads are similar to each other. Considering a simulation with per-node memory requirements near the node capacity of 32 GB, the 1 thread case is analogous to a hybrid code with 1 MPI process per UMA region, 1 thread per MPI process, and 8 GB per MPI process. The 4 thread case, with the placement shown in Table 2, is analogous to a hybrid code with 1 MPI process per node, 4 threads distributed over the UMA regions, and 32 GB of memory per MPI process. For these more realistic cases, reordering does improve the performance of the threaded assembly and solve steps.
The unthreaded sections of the code that access first-touch-distributed memory become slower as more memory is moved off the master thread’s UMA region (see Figure 9). This occurs for almost all sections of the code when moving from 1 to 2 threads and is especially obvious in the Adapt setup section (in the code this is the assemble_metric subroutine).
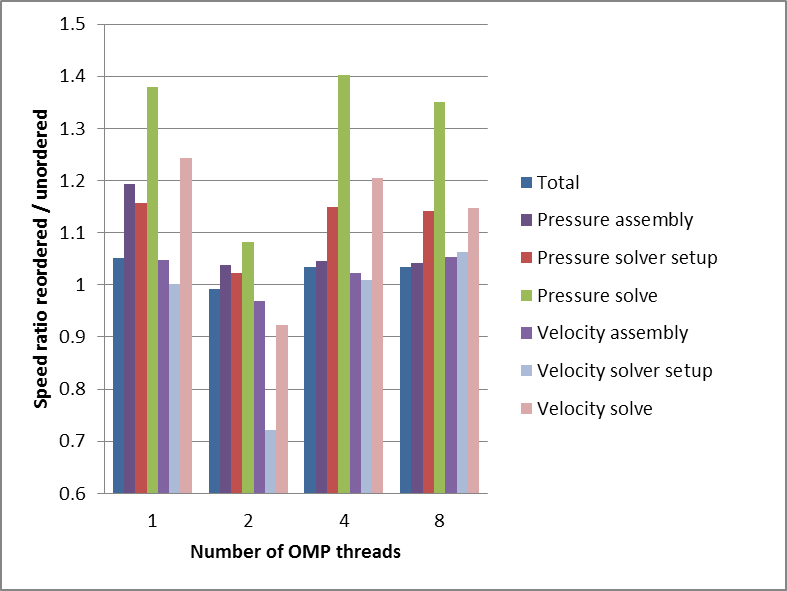
Figure 8: 3D backward-facing step flow (test
case backward_facing_step_3d) at
simulation time = 0.04 (= 20 time-steps followed by the first adapt step). Speed-up from reordering the mesh. Simulation size is ~1,000,000 nodes.
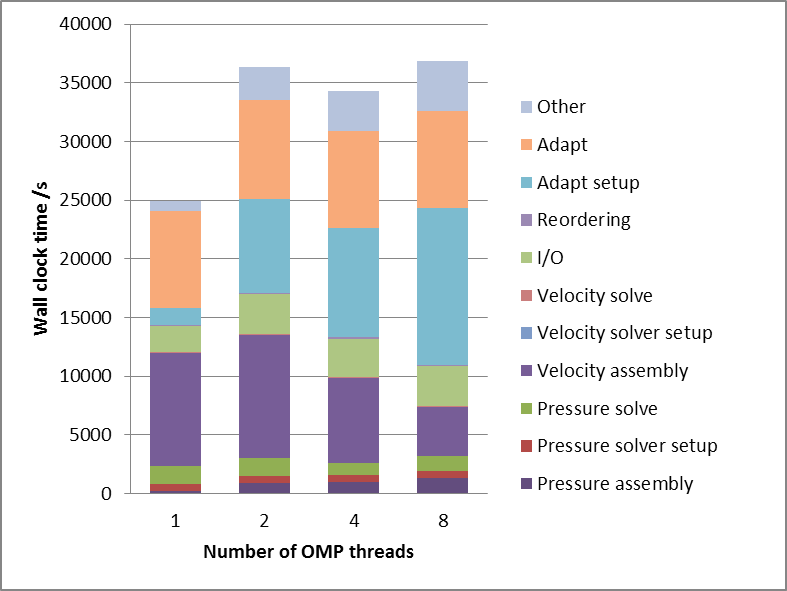
Figure 9: 3D backward-facing step flow (test
case backward_facing_step_3d) at
simulation time = 0.04 (= 20 time-steps followed by the first adapt step). Fraction of overall time spent in different
tasks. Note: the first adapt always takes
a long time; a more representative time for an adapt during the rest of the
simulation would be ~900 s. Simulation
size is ~1,000,000
nodes.
The usage of the centrally installed Fluidity binary on HECToR has been ~100,000 node hours (23,000 kAU) per year. Adding reordering to the code will reduce the kAU footprint by 5%, 1000kAU per year. Hilbert space-filling curve reordering could be applied to other finite element codes running on HECToR to give a similar improvement.
Reordering the computational mesh in Fluidity can give speed-ups compared with an unordered mesh of 5% overall and 5‒20% for assembly and solve but the problem size (per MPI process) has to be large to achieve this speed-up. Threading with first-touch initialisation in a NUMA system generally maintains this speed-up.
Acknowledgements
This project was funded under the HECToR Distributed Computational Science and Engineering (CSE) Service operated by NAG Ltd. HECToR – A Research Councils UK High End Computing Service - is the UK's national supercomputing service, managed by EPSRC on behalf of the participating Research Councils. Its mission is to support capability science and engineering in UK academia. The HECToR supercomputers are managed by UoE HPCx Ltd and the CSE Support Service is provided by NAG Ltd. http://www.hector.ac.uk
References
|
[1] |
D. A. Burgess and M.
B. Giles, “Renumbering unstructured grids to improve the performance of codes
on hierarchical memory machines,” Advances in Engineering Software, vol.
28, pp. 189-201, 1997. |
|
[2] |
S. Aluru and F.
Sevilgen, “Parallel domain decomposition and load balancing using space-
filling curves,” in Proc. 4th IEEE International Conference on High
Performance Computing, 1997. |
|
[3] |
G. Heber, R. Biswas
and G. R. Gao, “Self-avoiding walks over adaptive unstructured grids,” Concurrency:
Practice and Experience, vol. 12, pp. 85-109, 2000. |
|
[4] |
H. Liu and L. Zhang,
“Existence and construction of Hamiltonian paths and cycles on conforming
tetrahedral meshes,” International Journal of Computer Mathematics, vol.
88, no. 6, pp. 1137-1143, 2001. |
|
[5] |
A.-J. N. Yzelman and
R. H. Bisseling, “A cache-oblivious sparse matrix--vector multiplication
scheme based on the Hilbert curve,” in Progress in Industrial Mathematics
at ECMI 2010, Berlin, 2012. |
|
[6] |
H. Le, P. Moin and J.
Kim, “Direct numerical simulation of turbulent flow over a backward-facing
step,” Journal of Fluid Mechanics, vol. 330, pp. 349-374, 1997. |