Next: Transition state optimisation Up: Implementation and performance Previous: Implementation and performance Contents
The microiterative minimisation scheme in DL-FIND follows program logic similar to the original HDLCOpt implementation. The program flow of a microiterative minimisation with electrostatic embedding in DL-FIND is as follows:
Note that in the original HDLCOpt implementation the macroiterative step energy (i.e. the exact energy before the inner region step is taken) was used as a reference energy to test acceptance of the first microiterative step. This is acceptable for a minimisation because the energy should decrease in both the macroiterations and microiterations. However, the DL-FIND implementation is designed to work for methods where the energy may not decrease after a macroiterative step, so a reference ESP-approximated energy is calculated before any outer region steps are taken.
The main DL-FIND loop cycles once per energy evaluation. A flag (glob%imicroiter) is used to switch between
macroiterations and microiterations.
At the macroiterative step, a full QM/MM calculation is carried
out, as in a standard optimisation, by a call to the ChemShell QM/MM driver, giving an energy ![]() and gradient
and gradient
![]() .
In the same call the QM code
is then used to calculate the electrostatic potential on a van der Waals surface
around the QM region. A least-squares fit algorithm in ChemShell is used to fit point charges at the
QM atom positions to reproduce the ESP.
A second call to ChemShell is then made to recalculate the QM/MM energy and gradient using the point charge
representation for the QM atoms, giving
.
In the same call the QM code
is then used to calculate the electrostatic potential on a van der Waals surface
around the QM region. A least-squares fit algorithm in ChemShell is used to fit point charges at the
QM atom positions to reproduce the ESP.
A second call to ChemShell is then made to recalculate the QM/MM energy and gradient using the point charge
representation for the QM atoms, giving
![]() and
and
![]() ESP.
ESP.
Following Ref. [9], the corrected gradient
![]() and energy
and energy ![]() used in the microiterations are:
used in the microiterations are:
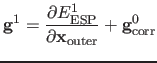 |
(1) |
and
| (2) |
where
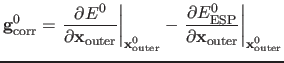 |
(3) |
where superscript 1 indicates the current coordinates and 0 the respective coordinates from the last macroiterative calculation. The expressions for the corrected energies and gradients ensure a smooth connection between the microiterative and macroiterative cycles, as in the case of identical geometries the equations reduce to the exact answer. In DL-FIND the corrections are actually calculated for the full set of coordinates (not just the outer coordinates), but the energy expression collapses to the outer coordinates because the inner region is fixed, and the gradient correction for the inner coordinates is not used by the microiterative optimiser.
DL-FIND supports multiple instances of the low memory BFGS (L-BFGS) minimisation algorithm, and two instances are used during
a microiterative minimisation. The first L-BFGS instance is used for macroiterative steps and covers all coordinates, although
only inner region steps are permitted during macroiterations. The reason it covers all coordinates and not just the inner region
is because the gradients on all atoms can then be taken into account when calculating the inner region step, and therefore
the outer region does not have to be completely converged during the microiterative cycles for the optimisation to succeed.
The second L-BFGS instance is initialised at the start of every microiterative loop and covers the outer region coordinates only.
The corrected QM/MM energy and gradient is used to relax the environment while the inner region is kept fixed. The
second L-BFGS data is kept in a separate set of arrays in the microiter module.
Unlike HDLCOpt, DL-FIND supports multiple coordinate systems and therefore special care must be taken during the microiterative cycles that the correct subset of coordinates are used. When the Cartesian coordinates used externally are transformed to the internal list of coordinates used by the optimiser, the new list is ordered into inner region coordinates followed by outer region coordinates. This makes it straightforward to operate over a single region. When Cartesians are used internally, this mapping is trivial. The delocalised coordinate (DLC) and total connection (TC) coordinate systems, however, may not be used, as they are delocalised over the entire system and therefore cannot be decomposed by region. Hybrid delocalised coordinates (HDLCs) and HDLC-TC may be used as they are only delocalised over discrete subsets of coordinates called residues, providing that no residues cross the inner and outer regions. The input is checked to ensure that this does not happen. In the HDLC case the list of internal coordinates is ordered by residue within each region.
A number of keywords were added to the DL-FIND input to specify that a microiterative optimisation should be carried out, the list of atoms or residues in the inner region, whether to carry out an ESP fit (a full QM calculation can also be used during the microiterations if requested), and the maximum number of microiterative cycles to carry out before taking another macroiterative step.
The microiterative minimisation scheme was tested for correctness on a QM glycine molecule solvated in water described by a classical forcefield. To check that the implementation gave similar performance improvements to the original HDLCOpt implementation, it was further tested on the water sphere system described in Ref. [9]. This consists of 4404 water molecules cut from equilibrated bulk water with a radius of 25 Å, as shown in Figure 1.
![\includegraphics[width=8cm,clip]{figures/water25_opt.eps}](img11.png)
|
Results for the optimisations are shown in Table 1.
| Active | Microiterative opt. | Standard opt. | |
||
| radius/Å | DOF | QM | MM | QM | kcal/mol |
| 5 | 2493 | 114 | 2018 | 639 | -2 |
| 10 | 6966 | 176 | 3230 | 2038 | +17 |
| 15 | 14382 | 311 | 4682 | 1372 | -3 |
| 20 | 26136 | 207 | 3949 | 1990 | +10 |
![\includegraphics[width=13cm,clip]{figures/watersphere_chart.eps}](img12.png)
|
Microiterative optimisations with HDLC coordinates and HDLC constraints were subsequently tested using the glycine-water system. The converged HDLC minima were in good agreement with those found using Cartesian coordinates.
Tom Keal 2013-06-04