The major bottleneck in a band-parallel calculation is the application of a band-by-band
transformation matrix to the wavefunction, so optimising these subroutines was the focus of this section of the work.
When band-parallelism is enabled in these transformations, there are two main drawbacks compared to the
alternative G-vector distribution:
- (a)
- No support for triangular matrices - Several key transformations are triangular, and whilst this is
exploited in a G-vector parallel calculations it is not in a band-parallel calculation.
- (b)
- Transformations require all-to-all communication amongst the cores in a band-group - Such communications
are not only time consuming, but scale as n
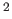for n-way band-parallel calculations.
Optimising these two aspects of the transformation is the key to obtaining good performance.
In general the transformation proceeds according to the following algorithm:
- At entry: each core holds its share of the wavefunction's bands, and the section of the transformation
matrix that is required to transform those bands; however in general the transformation will generate
contributions to all the bands of the wavefunction, not just the local share. These contributions must
be summed and communicated to the appropriate core.
- Each core selects a "client" core, and applies the subset of the transformation that generates
the contribution of the local bands to the client's transformed bands.
- The transformed data is sent to the client core (not necessarily directly).
- The core receives transformed data from other cores. All contributions to its local share of the transformed data are summed.
- Each core selects a different client core, and repeats steps 2-5 until all of the transformation has been applied and the data exchanged with the other cores.
- At exit: each core holds its share of the transformed wavefunction's bands
