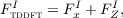
Abstract
Time-dependent density functional theory (TDDFT) is a formally exact method for calculating electronic excitations. In particular, linear-response TDDFT can be used to determine atomic forces in these excited states so that the structure and molecular dynamics can be probed. This report discusses the implementation of the above methods in CASTEP [2], one of the most popular electronic structure codes in use on HECToR. Making this functionality available opens up avenues for new science in a number of areas, including, but not limited to, photovoltaics and laser chemistry.
Time-dependent density functional theory (TDDFT) has become a well-established technique for modelling excited state properties in molecular systems, and has been implemented in several quantum-chemistry codes. An implementation of TDDFT in CASTEP [2] will give the UK electronic structure community an opportunity to address cutting-edge scientific problems in areas such as inorganic and organic photovoltaic materials, catalytic reactions at surfaces, light-emitting polymer materials for optical displays, and femtosecond laser chemistry. CASTEP in particular has an excellent record of use in high performance computing and is one of the most used codes on HECToR. The availability of TDDFT in CASTEP provides a platform for complementing a wide range of other property calculations at the same level of theory, within the same code. The implementation of hybrid functionals promises to address some of the limitations that have previously hindered the application of TDDFT to extended systems. [3, 1, 5]
This report is the second part of a 2-year dCSE project and focusses on an implementation for computing atomic forces in electronic excited states that are determined through linear response TDDFT in the Tamm-Dancoff approximation. For discussion on the iterative eigensolvers used in determining these excited states, please refer to the previous report available at http://www.hector.ac.uk/cse/distributedcse/reports/castep02/, and references therein.
Milestone 1 - Implement XC response kernel for hybrid functionals.
The work for this milestone has already been discussed in the previous dCSE report (http://www.hector.ac.uk/cse/distributedcse/reports/castep02/). In summary, the Hartree-Fock exchange contribution to the excitation energy, and its operation on a vector have been implemented, allowing available hybrid exchange correlation functionals to be used as an adiabatic exchange correlation kernel for TDDFT.
As discussed in the previous dCSE report on TDDFT in CASTEP, the eigensolvers have been tested on HECToR. However, problems were encountered when attempting to produce photoabsorption spectra of even moderately sized molecular systems (~ 50 atoms). Specifically, restarts of a TDDFT calculation with a large number of states (> 100) were unfeasibly long, reading in the order of 100GB data. Each TDDFT state requires an entire wavefunction object and all lower states are required to enforce the orthogonality of the next states. The cause of the bottleneck was in the code used to read in CASTEP wavefunction files from disk. This problem was addressed as part of another dCSE project “Boosting the scaling performance of CASTEP: enabling next generation HPC for next generation science”. In summary, a restart of a particular TDDFT calculation on HECToR that previously took ~ 2.5 hours to read in 100 files of 800MB size was reduced to approximately 15 minutes, a factor of 10 improvement.
Milestone 2 - Implement calculation of forces.
Computation of the atomic forces is performed by computing the derivative of the total energy with respect to each atomic coordinate. Following Hutter’s paper [4], computation of the forces needs to take in to account that a change in the Kohn-Sham orbitals also affects the response orbitals, complicating the derivative. The Lagrangian method used leads to three contributions to the forces: from the ground state orbitals, from the linear response TDDFT orbitals and from the so-called Z vector. The Z vector is “the matrix of Lagrange multipliers associated with the stationarity of the Kohn-Sham orbitals”. [4] This vector is akin to a response wavefunction and requires the solution of a Sternheimer-like equation. The ground state force contribution is, of course, already implemented in CASTEP, so we will omit this term in the following discussion. Therefore, the contribution to the force on atom I from TDDFT has two terms
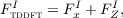 | (1) |
where FxI is the contribution from the TDDFT response orbital (referred to as x in Hutter’s paper and as Φ{-} in the previous dCSE report), and FZI is the contribution from the Z vector. In Dirac notation (Hutter’s formulation was written in a matrix element notation) the force terms are
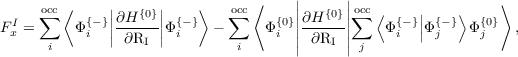 | (2) |
and
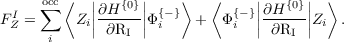 | (3) |
In the above equations, H{0} is the ground state Kohn-Sham Hamiltonian and RI is
the atomic coordinate of atom I. Note that the last term of equation 2 contains a
rotation in bands of the ground state wavefunction by the matrix with elements
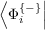 Φj{-}⟩
. The operator ∂H{0}∕∂RI was already implemented in CASTEP,
although care was needed to correctly implement the non-local pseudopotential
contribution.
Φj{-}⟩
. The operator ∂H{0}∕∂RI was already implemented in CASTEP,
although care was needed to correctly implement the non-local pseudopotential
contribution.
All of the objects above are available after a TDDFT calculation, except for the Z vector. This is determined according to the Sternheimer-like Handy-Schaefer Z vector equation
![| ⟩
(H {0} - εi)|Z *i⟩+ PcδVscf[n{z}]||Φ{i0} = |ui⟩,](TDDFT_forces4x.png) | (4) |
where εi are the Kohn-Sham eigenvalues, the projector on unoccupied unperturbed states, Pc, and Hartree-exchange-correlation response potential, δV scf, are defined in the previous dCSE report on this project (http://www.hector.ac.uk/cse/distributedcse/reports/castep02/). The new electron density-like object n{x} is
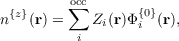 | (5) |
which can be computed using the existing first order response density routine for TDDFT. The wavefunction-like object u is
![{
{x}|| {0}⟩ {-} || {- }⟩
|ui⟩ = Pc δVscf[n ]|ϕi + δVscf[n ]|Φ i (6)
occ| ⟩ ⟨ | | ⟩ | ⟩ }
+∑ ||Φ{-} Φ{0}||δVscf[n{-}]||Φ {0} + V{2}[n{-}]||ϕ {0} .
j j j i xc i](TDDFT_forces6x.png)
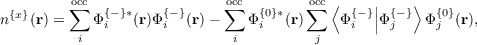 | (7) |
where, as in equation 2, there is a rotation in bands of the ground state wavefunction in the last term. The second order exchange correlation potential is obtained from the third (functional) derivative of the exchange correlation energy with respect to the electron density
 = drdr′-----δExc------|| n{-}(r′)n{-}(r′′).
xc δn(r)δn(r′)δn(r′′)|n{0}](TDDFT_forces8x.png) | (8) |
We evaluate this using a two-point finite difference of the first order exchange correlation response potential, δV scf[n{-}].
The Z vector equation (4) can be solved using the existing CASTEP density functional perturbation theory (DFPT) E-field solvers [7], replacing the idΦi{0}∕dkα term with ui. We employed the variational E-field solver in our prototype code, extending the functionality to take a general “perturbation”, rather than just the electric field. In order to keep the results consistent between two runs, it was found that the convergence tolerance for the E-field minimiser had to be tightened considerably for this use, from 10-5 to 10-8Å3. This is required because the initial trial wavefunctions are randomised. Such an extreme tolerance may be problematic because as a general rule of thumb, for the result to be accurate from the E-field solver, the ground state wavefunction needs to be converged to the square of the E-field tolerance. The full ramifications of this have yet to be explored.
The computed forces were tested for correctness by performing a numerical derivative of the excitation energy with respect to an atomic displacement, i.e. computing the excitation energy at two small atomic displacements and performing a two-point derivative. The resulting forces matched to within the error expected from the numerical derivative. This test was successfully performed for a set of small molecules. The hydrogen molecule was a particularly useful test case as the pseudopotential used was purely local. This allowed for separate testing of local and non-local pseudopotential contributions to the ∂H{0}∕∂RI operator.
Incorporating the TDDFT forces into the existing geometry optimiser required some careful consideration in terms of module dependencies. Specifically, the geometry module requires a total energy for the electronic state and the atomic forces for that state. Previously this was done only for the ground state, with the energy and forces being provided by the electronic and firstd modules, respectively. Through discussion with the CASTEP Development Group it was decided to have the tddft module called from electronic and firstd when the total energy or forces of an excited state is requested. However, the TDDFT code makes use of some of the higher level DFPT code in the secondd module, essentially using it in a way not envisioned in its initial code design, leading to some circular compilation dependancies. The secondd module (and one of its dependants, magres_utils) makes direct reference to routines in the electronic module. It was decided that the routines in question were more utilities in nature and would be moved from the electronic module to the low-level algor module, hence removing any circular dependancies.
A test calculation on the formaldehyde molecule was performed so that comparison with the results in Hutter’s paper could be made. Table 1 gives the comparative results. An exact match is not expected because Hutter’s work included the Martyna-Tuckerman method to decouple periodic images of the electrostatic potential [6], which is not implemented in CASTEP. Different pseudopotentials were also used. Those details aside, the geometries generated by CASTEP compare very well with the previously published results. It should be noted that in the case of the first excitation, the non-planar configuration is only obtained when the planar symmetry of the ground state geometry is broken by adding some random noise to the positions of the initial configuration. This is because the geometry optimisation algorithm can stop at stationary points in the energy landscape, not necessarily a global minimum. One expects the excited state energy landscape to be complicated even for small molecules therefore some care will have to be taken when running excited state geometry optimisations so as not to converge on metastable configurations. Developing more sophisticated geometry optimisation methods are outside the scope of this dCSE.
| Electron configuration | C–O | C–H | ∠ HCH | Φ |
| Ground state (Hutter) | 1.211 | 1.118 | 116.1 | 0 |
| Ground state (This work) | 1.208 | 1.120 | 116.1 | 0 |
| 1st singlet excitation (Hutter) | 1.308 | 1.103 | 116.8 | 30.0 |
| 1st singlet excitation (This work) | 1.305 | 1.103 | 117.5 | 28.9 |
| 2nd singlet excitation (Hutter) | 1.204 | 1.115 | 119.0 | 0 |
| 2nd singlet excitation (This work) | 1.203 | 1.114 | 120.4 | 0 |
In terms of performance, carrying out an excited state optimisation is more expensive than that for the ground state for a number of reasons. The obvious one is the added expense of solving the TDDFT eigenvalue problem at each trial geometry. Another is that the energy tolerance used to determine the ground state wavefunction needs to be tighter when used in conjunction with a linear response method. This is in order to guarantee the accuracy of the response wavefunctions and therefore increases the number of iterations to obtain the ground state. The computation of the TDDFT forces is also not near negligible compared to solving the eigenvalue problem, as is the case in the ground state. To obtain the Z vector, an extra calculation equivalent to a one-shot, single-direction E-field DFPT run is required, comparable in computation time to the ground state calculation in our tests. However the single longest step is still obtaining the TDDFT eigenvalues/vectors. This step could be reduced by using the TDDFT eigenvectors from the previous geometry iteration as the starting point for the current one. Of course, care must be taken to preserve normalisation and othogonality to both the (new) ground state and between the eigenvectors themselves. An implementation of this reduced the number of iterations used by the TDDFT solver by a factor of at least two in our tests. Some stability can be gained by adding a small random component (0.001) to the previous eigenvector, thus ensuring the initial trial vector spans the required subspace. In our tests this did not increase the number of TDDFT iterations. Using the earlier formaldehyde case as an example, the time for the structure optimisation of the 2nd excited state in 7 BFGS iterations was reduced by 40% when compared to randomised initial trial eigenvectors.
Milestone 3 - Implement Born-Oppenheimer molecular dynamics.
With the code abstraction already employed in the prototype TDDFT geometry optimisation, Born-Oppenheimer molecular dynamics of an excited state is already in place, but has yet to be tested. A potential issue beyond the scope of this dCSE is that of excited state crossings that are almost certain to occur during the course of a calculation.
The importance of working with a well structured and documented code cannot be emphasised enough. Throughout this project it was found that similarities with existing methods meant that code originally written for a specific purpose in CASTEP could be used more generally with little (or occasionally no) further code modification. This is thanks to the high coding standards used in the CASTEP source. In the cases where changes were required for existing code, the work was expedited greatly by the documentation in the subroutine headers and clear comments throughout.
Also invaluable during code development was the availability of a CVS mirror of the main CASTEP source. This allowed work to be done on a branch of the code base while being able to pull in changes from major version releases. Subsequent migration of the CASTEP repository to the Mercurial versioning system makes such a process even easier for the coder.
The modular nature of the code introduced during this dCSE means that improvements to the geometry optimisation methods from the recent LBFGS dCSE project can immediately be taken advantage of in TDDFT calculations. It is hoped that in adhering to CASTEP coding standards that at least some of the code developed during this dCSE will be used for unforeseen functionality in the future. As an extension to this project, it is already planned to integrate the TDDFT forces work with CASTEP’s existing finite-displacement phonon code, allowing investigation of vibrational properties of systems in an electronic excited state.
A demonstration project based on polyfluorene is under way. This conjugated polymer is of interest as a material for organic light emitting diodes that can be colour tuned. Results will be reported in due course.
The code developed during this dCSE project will be merged with the main CASTEP source for a future major version release. Access to a beta of the TDDFT code is available to licensed CASTEP users upon request, contact Keith Refson at keith.refson@stfc.ac.uk.
This project was funded under the HECToR Distributed Computational Science and Engineering (CSE) Service operated by NAG Ltd. HECToR - A Research Councils UK High End Computing Service - is the UK’s national supercomputing service, managed by EPSRC on behalf of the participating Research Councils. Its mission is to support capability science and engineering in UK academia. The HECToR supercomputers are managed by UoE HPCx Ltd and the CSE Support Service is provided by NAG Ltd. http://www.hector.ac.uk
[1] L. Bernasconi, M. Sprik, and J. Hutter, Hartree-Fock exchange in time dependent density functional theory: application to charge transfer excitations in solvated molecular systems, Chemical Physics Letters 394 (2004), no. 1-3, 141–146.
[2] S.J. Clark, MD Segall, CJ Pickard, PJ Hasnip, MJ Probert, K. Refson, and MC Payne, First principles methods using CASTEP, Z. Kristallogr 220 (2005), no. 5-6, 567–570.
[3] A. Dreuw, J.L. Weisman, and M. Head-Gordon, Long-range charge-transfer excited states in time-dependent density functional theory require non-local exchange, The Journal of Chemical Physics 119 (2003), 2943.
[4] J. Hutter, Excited state nuclear forces from the Tamm–Dancoff approximation to time-dependent density functional theory within the plane wave basis set framework, The Journal of Chemical Physics 118 (2003), 3928.
[5] A.F. Izmaylov and G.E. Scuseria, Why are time-dependent density functional theory excitations in solids equal to band structure energy gaps for semilocal functionals, and how does nonlocal Hartree–Fock-type exchange introduce excitonic effects?, The Journal of Chemical Physics 129 (2008), 034101.
[6] G.J. Martyna and M.E. Tuckerman, A reciprocal space based method for treating long range interactions in ab initio and force-field-based calculations in clusters, The Journal of Chemical Physics 110 (1999), 2810.
[7] K. Refson, P.R. Tulip, and S.J. Clark, Variational density-functional perturbation theory for dielectrics and lattice dynamics, Physical Review B 73 (2006), no. 15, 155114.
1This is a corrected form of Hutter’s equation 44, where the minus sign preceding the second term was omitted.