ScaLAPACK Performance

The performance of the distributed diagonaliser (PZHEEV) was compared to that of the LAPACK routine ZHEEV for a range of matrix sizes.

Table 5.1: Hermitian matrix diagonalisation times for the ScaLapack subroutine PZHEEV.

	time for various matrix sizes
cores	1200	1600	2000	2400	2800	3200
1	19.5s	46.5s	91.6s	162.7s
2	28.3s	65.9s	134.6s
4	15.8s	38.2s	54.7s	90.1s
8	7.9s	19.0s	37.6s	63.9s	81.6s
16	4.3s	10.5s	20.3s	32.5s	76.2s
32	2.7s	6.0s	11.6s	19.2s	43.1s

An improved parallel matrix diagonalisation subroutine, PZHEEVR^5.1, was made available to us by Christof Vömel (Zurich) and Edward Smyth (NAG). This subroutine consistently out-performed PZHEEV, as can be seen from figure 5.1.

Figure 5.1: A graph showing the scaling of the parallel matrix diagonalisers PZHEEV (solid lines with squares) and PZHEEVR (dashed lines with diamonds) with matrix size, for various numbers of cores (colour-coded)

The ScaLAPACK subroutines are based on a block-cyclic distribution, which allows the data to be distributed in a general way rather than just by row or column. The timings for different data-distributions for the PZHEEVR subroutine are given in table 5.2.

Table 5.2: PZHEEVR matrix diagonalisation times for a 2200x2200 Hermitian matrix distributed in various ways over 64 cores of HECToR.

Cores used for distribution of
Rows	Columns	Time
1	64	6.48s
2	32	6.45s
4	16	5.80s
8	8	5.92s

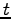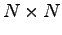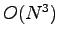The computational time $t$ for diagonalisation of a $N\times N$ matrix scales as $O(N^3)$, so we fitted a cubic of the form

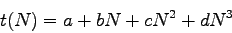$$t(N) = a + bN + cN^2 + dN^3$$ (5.1)

to these data for the 8-core runs. The results are shown in table 5.3. This cubic fit reinforces the empirical evidence that the PZHEEVR subroutines have superior performance and scaling with matrix size, since the cubic coefficient for PZHEEVR is around 20% smaller than that of the usual PZHEEV subroutine.

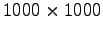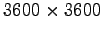Table 5.3: The best-fit cubic polynomials for the PZHEEV and PZHEEVR matrix diagonalisation times for Hermitian matrices from $1000\times 1000$ to $3600\times 3600$ distributed over 8 cores of HECToR.

Coefficient	PZHEEV	PZHEEVR
a	-1.43547	-0.492901
b	0.00137909	0.00107718
c	9.0013e-08	-7.22616e-07
d	4.31679e-09	3.53573e-09