


Next: Rotations
Up: Wave
Previous: Wave
Contents
The (S-)orthonormalisation and subspace diagonalisation operations
both require dot products between all pairs of bands. In the case of
the (S-)orthonormalisation the overlaps are between all pairs of bands
of a wavefunction, and so the result is Hermitian. For the subspace
diagonalisation the dot-product is between each band of a wavefunction
with each band of a different wavefunction - in fact since the second
wavefunction is the result of a Hermitian operator applied to the
first wavefunction the result should also be Hermitian, though at the
moment we do not exploit this4.1.
We distribute this by passing our data 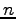 places to the right, and
receiving data from
places to the right, and
receiving data from 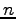 places to the left, and dotting the received
data with our local data. Then we increment
places to the left, and dotting the received
data with our local data. Then we increment 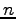 by 1 and repeat the
process until
by 1 and repeat the
process until 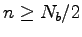 .
.
Sarfraz A Nadeem
2008-09-01
![]() places to the right, and
receiving data from
places to the right, and
receiving data from ![]() places to the left, and dotting the received
data with our local data. Then we increment
places to the left, and dotting the received
data with our local data. Then we increment ![]() by 1 and repeat the
process until
by 1 and repeat the
process until ![]() .
.