Final Report

Numerical Algorithms Group Ltd
Parallel Software Development Project

Uncertainty Quantification using Differential Geometric Population MCMC

Ben Calderhead^∗1, Gary Macindoe² and Mark Girolami^†2

¹CoMPLEX, University College London, UK
²Department of Statistical Science, University College London, UK

9^th August 2013

Contents

1 Project Overview and Summary

2 Introduction

2.1 Motivating Scientific Examples
2.2 Benchmark Models
2.3 Cluster Configuration and Compiler Settings
2.4 Key Objectives

3 Work Package 1

3.1 Results

4 Work Package 2

4.1 Results

5 Uptake and Dissemination of Software

6 Conclusions and Future Work

^*Gratefully acknowledges support through the EPSRC “2020 Science” Fellowship Programme.

^†Gratefully acknowledges support through the EPSRC Established Career Research Fellowship EP/J016934/1 and a Royal Society Wolfson Research Merit Award.

1 Project Overview and Summary

Uncertainty quantification is vital in many scientific areas. In particular, the Bayesian approach provides a consistent inductive logic for reasoning about systems where measurements and models contain often high degrees of uncertainty. A number of competing hypotheses regarding the underlying structure of a system of interest can be encoded as mathematical models, and we may use this Bayesian statistical framework to decide systematically which model is best supported by the observed data and may therefore be best employed for predictive purposes.

This project developed an efficient C implementation of a parallel Differential Geometric Markov Chain Monte Carlo (MCMC) sampler within a general population MCMC framework using MPI. This state of the art statistical methodology allows key Bayesian quantities to be accurately estimated by drawing samples from a sequence of tempered probability distributions bridging from the prior to the posterior. The posterior probability distribution gives estimates of unknown parameter values in the statistical model given the available data, and samples from the additional tempered distributions may be used to estimate the marginal likelihood for comparing models.

The software developed enables systematic comparison of model hypotheses for systems described using coupled systems of nonlinear differential equations, such as gene regulatory networks, and systems described using aggregated Markov processes, such as ligand-gated ion channel mechanisms in the biological sciences. This software can be deployed on any modelling problem where nonlinear differential equations or Markov processes are used and as such has the potential to have a widespread impact especially as the size and complexity of such models is growing.

The C codes in this project deliver scalable performance, which is up to 2 orders of magnitude faster than the original Matlab implementation. Further, its modular design allows it to be easily extended to enable statistical inference over additional classes of models thus ensuring it widespread utility to practising scientists and engineers.

2 Introduction

The quantification of uncertainty is now being widely recognised as essential to the enquiry and development process in the fields of science and engineering¹. Such approaches drive a wide range of decision-making within industry, academia and government, and there is consequently a very strong demand for software to support this aim. In particular, the use of Bayesian methodology for making predictions and quantifying uncertainty both in data and models has massively increased over the last 15 years, in part due to the increased computing power available. Alongside this increase in computational ability, advances in Bayesian algorithms also play a significant role in making inference more feasible over complex statistical models.

The Bayesian paradigm involves representing unknown variables or parameters of a statistical model in terms of probability distributions, which are then updated according to the rules of conditional probability (Bayes Rule) to take into account the available data. This approach provides a consistent inductive logic for reasoning about systems where measurements and models often contain high degrees of uncertainty. The main scientific question that we wish to answer may be posed as follows: Given a number of competing hypotheses regarding the underlying structure of a system, how may we decide which statistical model is best supported by the observed data and may therefore be best employed for predictive purposes? The Bayesian approach offers a systematic and quantitative way of answering this, whilst avoiding overfitting to the data. However, such an approach is computationally intensive; rather than calculating a single value via optimisation, the answer instead takes the form of a probability distribution, which must then be integrated to obtain the required marginal likelihood for model comparison. For more realistic nonlinear models the resulting densities and integrals are generally not analytic and must be approximated.

Markov chain Monte Carlo (MCMC) methods allow samples to be drawn from arbitrary probability distributions and therefore provide a general approach to performing Bayesian analysis for wide classes of statistical models. In this project we have produced efficient parallelised C code which translates the original Matlab implementation of state-of-the-art MCMC methodology based on incorporating the Riemannian geometry induced by the statistical model of interest. This ``Differential Geometric MCMC'' methodology uses geometric information to explore the target distribution up to 2 orders of magnitude more efficiently than previous state-of-the-art MCMC methods, particularly for high dimensional and strongly correlated densities. However, despite this dramatic improvement in statistical efficiency the original Matlab code was still too slow to allow realistically complex models to be analysed within a reasonable timeframe.

This C code delivers the capability of allowing such models to be analysed within a Bayesian framework in hours rather than days by exploiting the speed-ups that may be obtained through parallelisation on a High-Performance Computing Cluster using MPI and OpenMP.

¹ The NSF and SIAM in the USA are supporting national initiatives in formalising research in Uncertainty Quantification. Likewise the EPSRC in the UK has recently funded a large Programme grant on Uncertainty Quantification in engineering inverse problems led by Prof. A. Stuart, University of Warwick, of which M.A. Girolami is a co-investigator EP/K034154/1

2.1 Motivating Scientific Examples

We chose particular scientific applications to be the motivating examples for driving this software development; biochemical models described by nonlinear differential equations and ligand-gated ion channel models described by aggregated Markov processes. These examples are based on current active research areas within Computational Statistics (and collaborators) at UCL, and have the potential to make a large impact within in the wider international research community. The software's framework has been designed to be general enough to allow arbitrary models to be analysed by specifying functions defining their likelihood and corresponding geometric quantities. This allows the computer code to be easily extendible to other statistical and scientific applications in the physical sciences and engineering.

2.2 Benchmark Models

Two differential equation models were used for benchmarking the improvement in speed over the original Matlab code. The Fitzhugh-Nagumo model consists of a system of nonlinear differential equations with 3 parameters and 2 initial conditions, resulting in a 5 dimensional probability distribution to be inferred. 1000 data points were generated from this model by solving the system with parameters [0.2, 0.2, 3] and initial conditions [-1, 1], and then adding Gaussian distributed perturbations to simulate noise. The full details of this model may be found in [1]. The second nonlinear differential equation model describes a circadian biochemical network in the plant Arabidopsis thaliana, which consists of 22 parameters and 6 initial conditions and results in a 28 dimensional probability distribution to be inferred. 10 data points were generated for each species (in order to simulate realistic experimental data) by solving the system using the parameter values detailed in [2], where full details of the model may also be found. In both cases, the standard deviation of the noise was chosen to be 1 percent of the standard deviation of the model output for each species.

We also considered an ion channel model described by an aggregated Markov process. The Markov process used consists of 5 states with 10 parameters, the full details of which are available in [3]. A dataset consisting of 6700 data points was generated to represent a realistically sized data set for the purpose of benchmarking.

The settings for the population MCMC sampler are described in the Sections 2 and 3, and the test scripts and datasets are also included in the code release for reproduction of results.

2.3 Cluster Configuration and Compiler Settings

All benchmarks were performed on the Statistical Science Computer Cluster at UCL. This cluster consists of 52 nodes, each with 2 quad-core 2.7GHz Opteron AMD processors with 8GB of memory. The nodes are connected using 10Gbit ethernet and based around the open source linux distribution Rocks 5.3 (http://www.rocksclusters.org). Our software was compiled using gcc version 4.1.2 with LAPACK version 3.4.2, which includes BLAS and CBLAS, and with the ODE solver package Sundials version 2.5.0. We also used OpenMPI version 1.6 to enable parallelism on the cluster. The following flags were employed during compilation:

-std=c99 -pedantic -Wall -Wextra -march=opteron -02 -pipe

2.4 Key Objectives

The main objectives for this project were as follows:

· Implementation of test suite for MCMC update functions.

· C implementation of MCMC update functions using OpenMP.

· C implementation of population MCMC using MPI.

· Matlab and R wrappers to run the developed C code.

The first three of these objectives were successfully completed resulting in a usable C implementation that offers up to 2 orders of magnitude speed improvement over the original Matlab code. The last objective of writing wrappers to allow Matlab and R to directly run the C code was not achieved due to time constraints, however this would be a useful addition for future work. In the following sections, an overview of each of these objectives is given in the order they appear in the work packages. The outcomes of the key objectives and resulting speed improvements compared with the baseline Matlab code are also presented.

3 Work Package 1

The first task involved refactoring the existing Matlab code and planning the structure of the C implementation. The MCMC update functions were then implemented in C using OpenMP to accelerate the computation using multiple cores. It was decided not to implement the Matlab wrappers at this stage, but to leave all interfaces to other software packages until the end of Work Package 2, once the full sampler had been implemented in C. This decision was taken to ensure we would have time to deliver a fully working piece of software coded entirely in C and took into account the reviewers' comments of our original proposal, where it was mentioned that delivering the wrappers for Matlab and R, in addition to the entire C implementation, would be rather ambitious. This proved to be a wise decision, as we eventually ran out of time to deliver the wrappers, but did successfully complete a fully working sampler in C, which we describe further in Work Package 2.

Unit tests were written to ensure correct outputs from the MCMC update functions were obtained after being rewritten in C. In particular, tests were written to confirm correct model outputs, likelihood functions and geometric information required for the MCMC sampler, such as gradients and metric tensors, for 100 randomly chosen inputs and the required tolerance for passing each test was set to 1e-6. The test suite was fully automated in CUnit using random inputs and their corresponding outputs generated from the original Matlab code.

3.1 Results

For this work package, the C implementations of the MCMC update functions were compared against the corresponding update functions in Matlab for each of the benchmark models. The update functions calculate the likelihood function of each model for a given set of parameters and dataset, along with gradient and geometric quantities required for the sampler. Timings were averaged over 1000 different parameter sets and performed on 4 cores using OpenMP enabled code. These functions represent the main workload of a Monte Carlo sampler, as they must be evaluated many hundreds of thousands of times.

Model	Matlab (sec)	C (sec)	Speed Improvement
10 Parameter Ion Channel	0.250678	0.003683	x68
5 Parameter ODE	0.061808	0.001818	X33
28 Parameter ODE	0.106800	0.019113	X6

4 Work Package 2

The main item of work in this section was the development of the full population MCMC framework in C using MPI, which utilises the MCMC update and likelihood functions developed in Work Package 1. The outputs of the software are samples drawn from a posterior probability distribution, and summary statistics (mean and standard deviation) of these outputs were checked against those obtained from the original Matlab code to ensure correctness of the overall algorithm. This part of the algorithm was structured in a modular form that allows additional ODE and aggregated Markov models to be quickly added, as well as enabling easy integration of different classes of models in the future.

An additional item in this Work Package was the development of wrapper codes for accessing the accelerated C code from Matlab and R. Unfortunately this was not possible to achieve within the timeframe of the project, however we were able to include the functionality that the software output can be saved in a native Matlab and R-readable format for easy post-processing of results.

4.1 Results

We first compared the performance of our C code with the original Matlab code using the ion channel model, where baseline performance is given by the Matlab code running on a single core. We observed that the C code offers much higher performance, as we might expect from the results in Work Package 1, and exhibits better efficiency than Matlab when scaled up to 8 cores, as shown in Figure 1. Of course the advantage of a C implementation is that we may use many more cores for computation, without the need for expensive Matlab toolboxes to allow this. Figure 2 demonstrates the scaling efficiency up to 100 cores, where performance is 60 times better than using a single core.

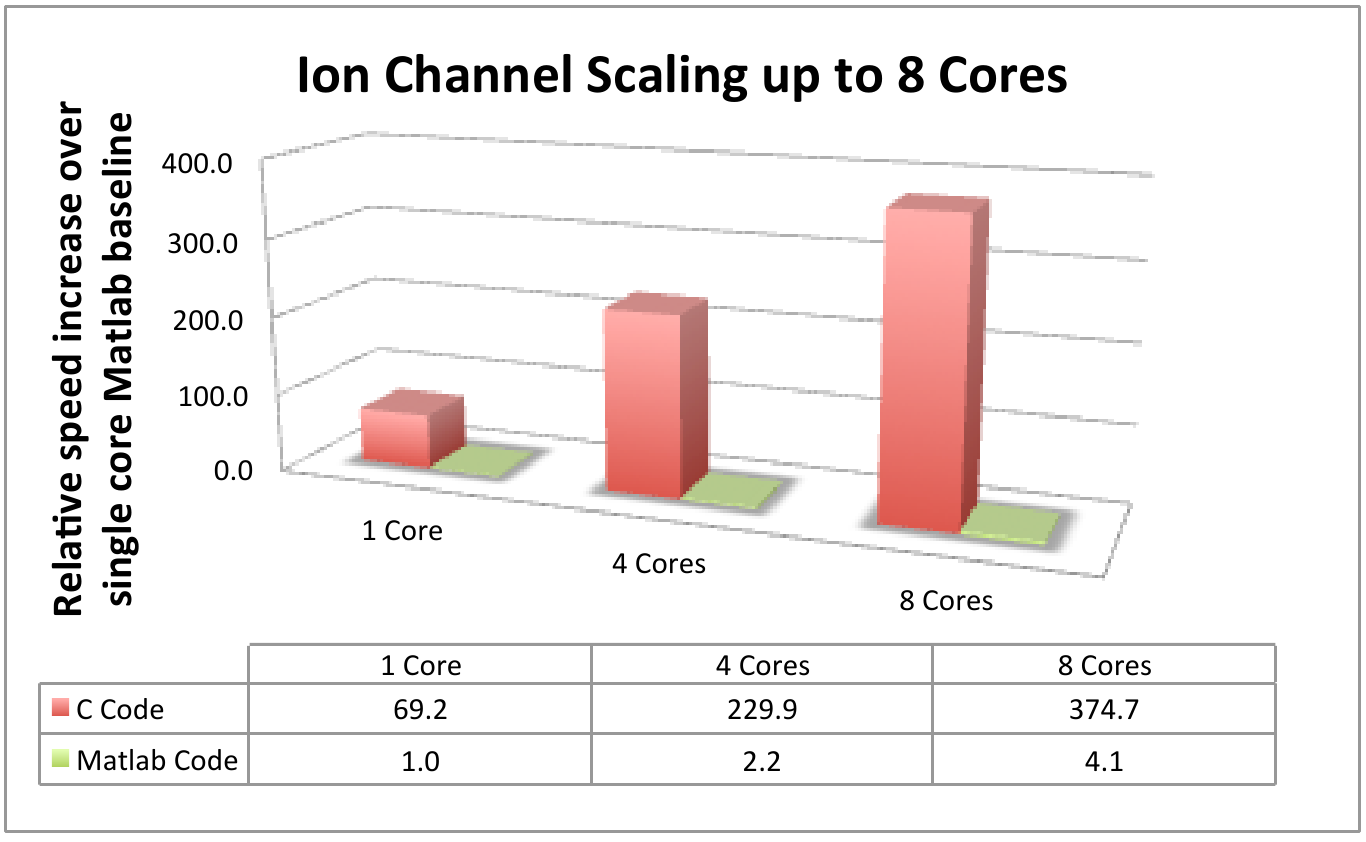
Figure 1: Comparative results using the ion channel model with single core Matlab as the baseline performance measure.

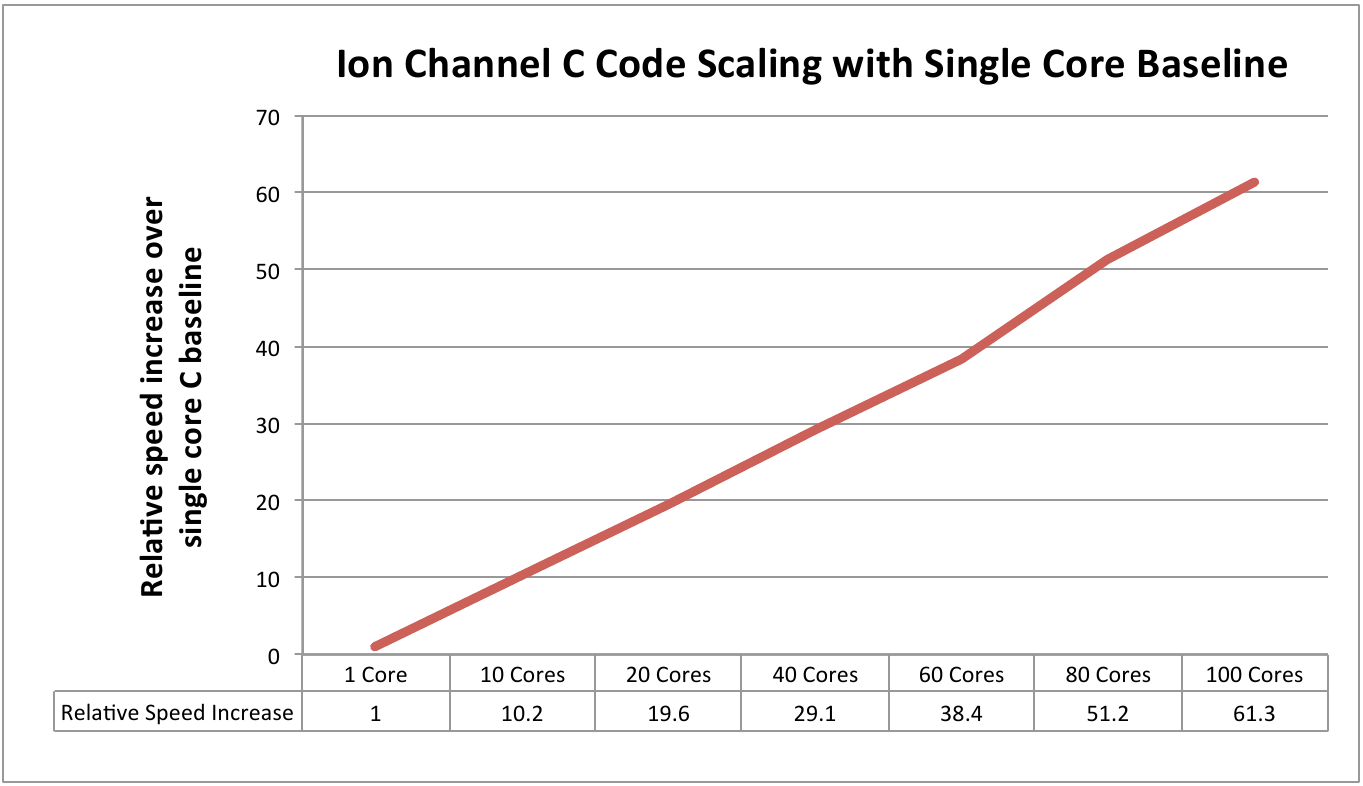
Figure 2: Scaling performance using the ion channel model with single core C as the baseline measure.

We also compared the performance of our C implementation using the two ODE model benchmarks. Figure 3 shows the scaling of the Fitzhugh Nagumo model with 5 parameters, compared to Matlab on up to 8 cores. Once again, above the increase in speed due to the likelihood and geometry calculations, the performance of the C implementation also scales more efficiently, as shown in Figure 4. Finally, we observed that the efficiency of our largest ODE model with 28 parameters across increasing numbers of cores scaled in a similar manner to the previous two example models, as may be seen in Figure 5. In all cases the communication overhead is perhaps fairly large relative to the individual computation on each core, and so we might expect this performance to improve as we consider larger models in future.

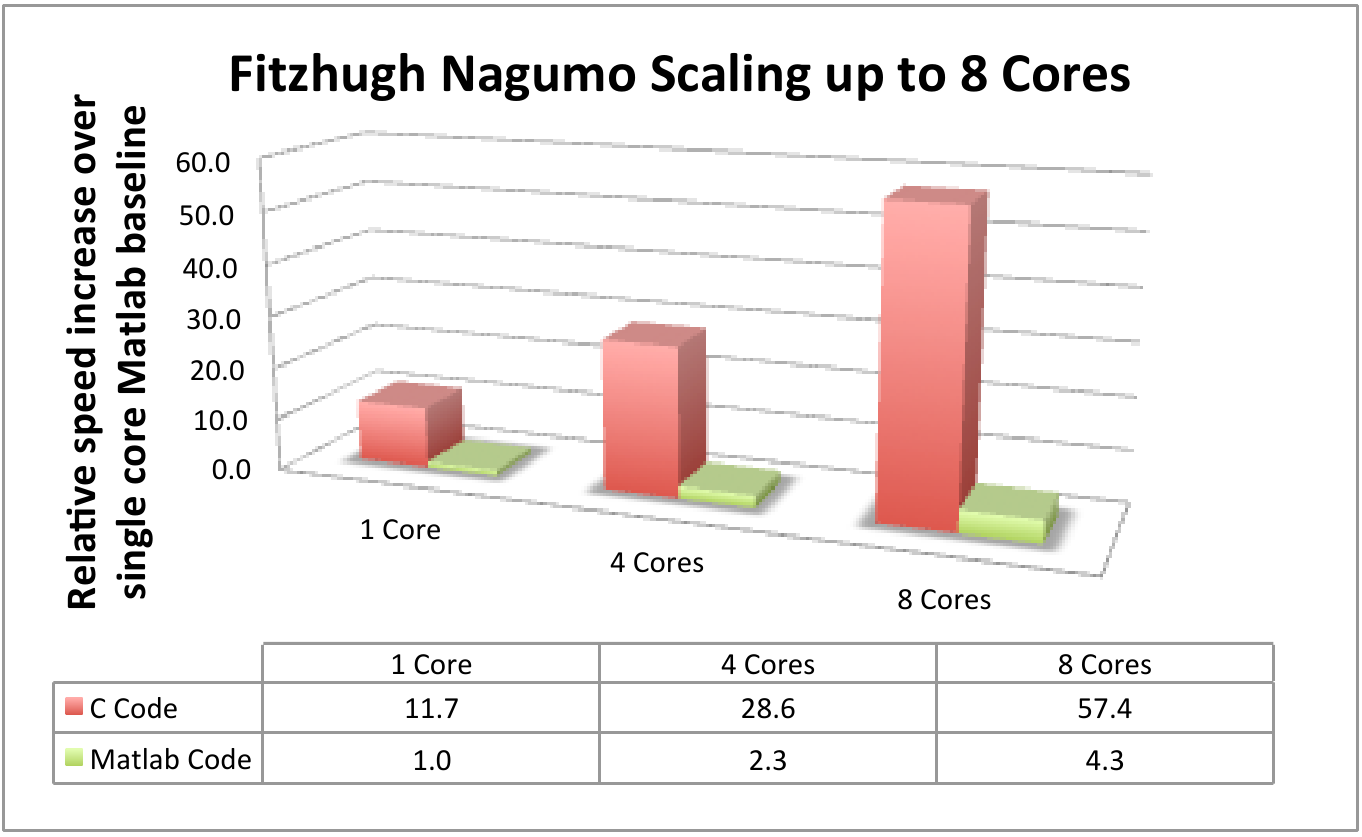
Figure 3: Comparative results using the Fitzhugh Nagumo model with single core Matlab as the baseline performance measure.

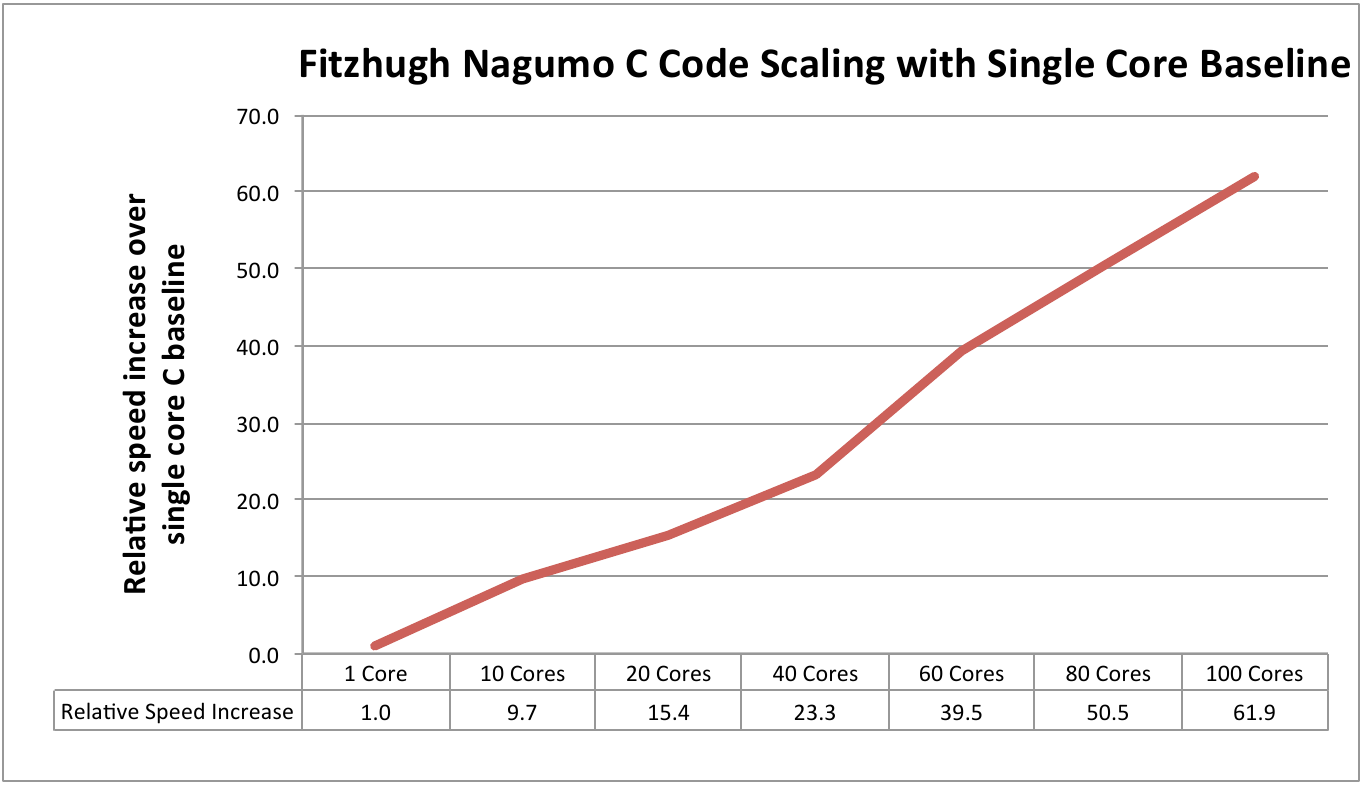
Figure 4: Scaling performance using the Fitzhugh Nagumo model with single core C as the baseline measure.

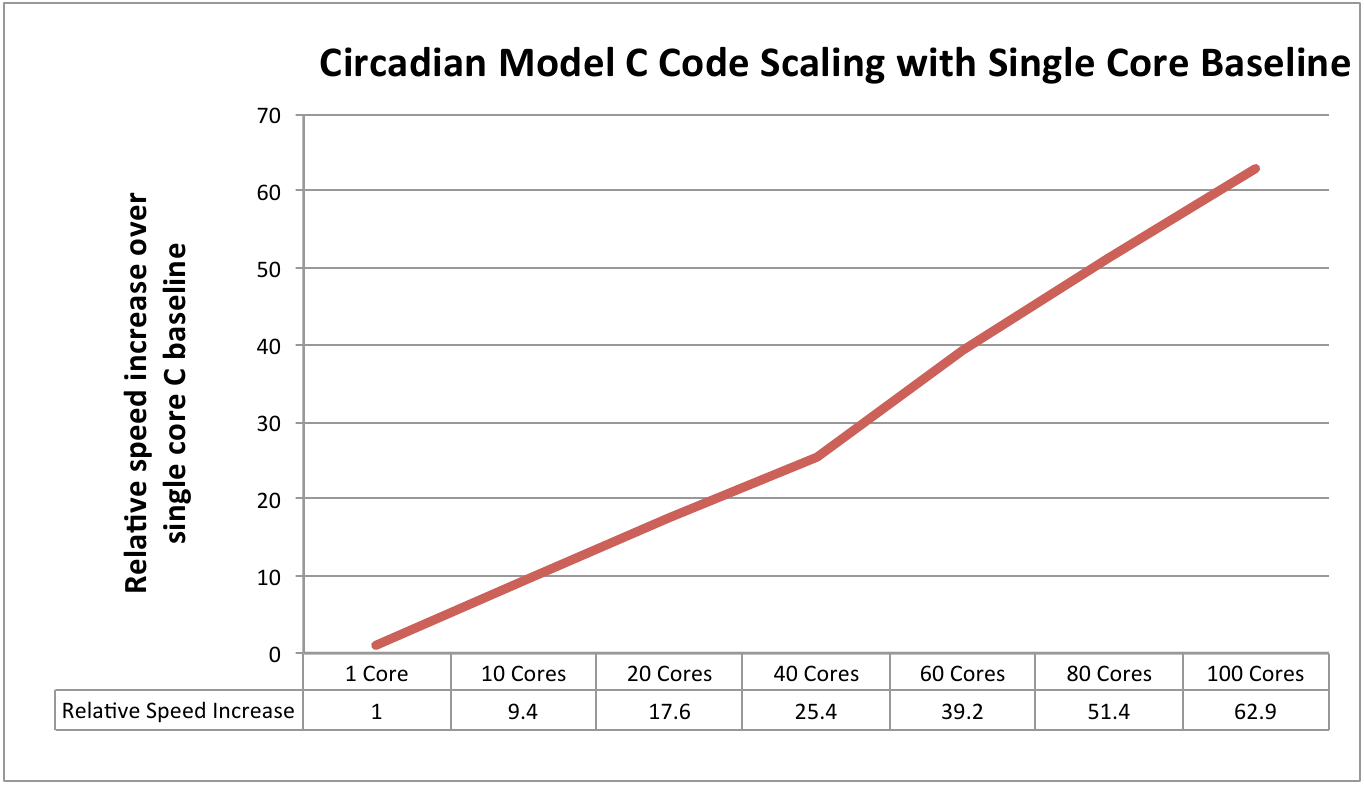
Figure 5: Scaling performance using the Circadian model with single core C as the baseline measure.

It is worth noting that these results will have a real and immediate impact on increasing the rate at which many of our motivating scientific questions may be answered; for example, our C implementation can now generate 100,000 samples for the Circadian model with 100 Markov chains in around 1 hour using 100 cores, whereas the fastest previous Matlab version would take around 2 days with 8 cores. This offers a significant advantage when there are large numbers of structural hypotheses to be tested and compared.

5 Uptake and Dissemination of Software

The C implementation we have developed is already being used in a number of projects and collaborations involving Prof. Girolami and Dr. Calderhead. It is currently being used in a number of work packages within ASSET (Analysing and Striking the Sensitivities of Embryonal Tumours), a 14 partner collaborative European project “tackling human diseases through systems biology approaches”, see http://www.ucd.ie/sbi/asset/for more details. The researchers involved in this work include Prof. Mark Girolami (Statistical Science, UCL), Prof. Heinrich Kovar (Children's Cancer Research Institute, Vienna), and Prof. Walter Kolch (Systems Biology Ireland).

This software is also currently being used in a collaboration between Prof. Girolami, Dr. Ben Calderhead (CoMPLEX and Statistical Science, UCL), Dr. Lisa Hopcroft (Paul O'Gorman Leukaemia Research Centre, Glasgow), and Prof. Tessa Holyoake (Paul O'Gorman Leukaemia Research Centre, Glasgow) to perform model comparisons of hypothesised biochemical systems implicated in chronic myeloid leukaemia.

We will also be presenting our software to a number of academic groups at universities in UCL, Warwick, MIT and Heriot-Watt over the coming months, from whom we obtained letters of support for our original application.

Further, we have plans in place to bring this software and methodology to a wider audience through publications in internationally leading journals. We are currently writing a paper for submission to the Journal of Statistical Software, as well as an application paper regarding differential equations to be submitted to the biological journal Bioinformatics and another application paper regarding ion channel models for submission to Nature Protocols. This will ensure the widest range of exposure to both statisticians and biologists who may be interested in using this software.

6 Conclusions and Future Work

We have successfully developed a differential geometric population MCMC framework in C and demonstrated the scalability and improvements in speed it offers compared to the original Matlab code. In particular, the software has enabled up to 2 orders of magnitude increase in speed compared to the maximum 8 core implementation that was previously possible in our original Matlab code. This software is already having a significant impact in Europe-wide projects and is expected to greatly increase the pace of scientific research in the motivating scientific areas.

Future work will involve developing interfaces to allow use of the C code from Matlab and R, thus widening the audience.

This project was funded under the HECToR Distributed Computational Science and Engineering (CSE) Service operated by NAG Ltd. HECToR – A Research Councils UK High End Computing Service - is the UK's national supercomputing service, managed by EPSRC on behalf of the participating Research Councils. Its mission is to support capability science and engineering in UK academia. The HECToR supercomputers are managed by UoE HPCx Ltd and the CSE Support Service is provided by NAG Ltd. http://www.hector.ac.uk

References

[1] Riemann Manifold Langevin and Hamiltonian Monte Carlo Methods, M. Girolami and B. Calderhead, Journal of the Royal Statistical Society: Series B (with discussion) (2011), 73(2):123-214

[2] Statistical analysis of nonlinear dynamical systems using differential geometric sampling methods, B. Calderhead and M. Girolami, Journal of the Royal Society Interface Focus (2011), 1(6):821-835

[3] Bayesian Approaches for Mechanistic Ion Channel Modeling, B. Calderhead, M. Epstein, L. Sivilotti and M. Girolami, in “In Silico Systems Biology”, Methods in Molecular Biology: Methods and Protocols, Springer