 |
Chris N. Richardson1
Garth N. Wells2
Date: 10 August 2013
The key aims of this project were to enhance the applicability and usability of DOLFIN, the core finite element library in the FEniCS Project, on parallel architectures. DOLFIN already supported fully distributed computation via MPI, but lacked some important infrastructure for enabling large scale parallel computation. This included a lack of (i) scalable parallel I/O and (ii) parallel mesh refinement. In addition, (iii) DOLFIN did not support threaded operations in combination with MPI. Implementation of the three aforementioned points formed the objectives of this project. All three objectives have been realised and exceeded, and the computer code developed is publicly available. Outcomes of this project are either already in a release of DOLFIN or are in development repositories and will be included in the next release, and are already being used in a number of research projects, including projects supported by UK research councils.
This report summarises the outcomes of the Distributed Computational Science and Engineering project `Expressive and scalable finite element simulation beyond 1000 cores'. This project aimed to add to and enhance parallel functionality in the open-source finite element library DOLFIN [2,1], which is a component of the FEniCS Project [3] (http://www.fenicsproject.org). Three areas were identified for development in this project to improve DOLFIN in parallel. The three areas were:
When solving equations using the finite element method, equations are integrated over individual cells (elements), yielding a small dense matrix or vector. The process of assembly is the insertion of these small matrices/vectors into a global vector or sparse matrix. The objective of this work package was to build on existing MPI-based and OpenMP-based parallelism for this process to develop support for hybrid OpenMP/MPI assembly, with processes distributed across compute nodes using MPI, and threads used on multi-core nodes (possibly with a small number of MPI processes). The primary motivations are to reduce the memory overhead associated with multiple MPI processes, and to map better onto linear solvers that are known to work best when threaded (e.g. LU solvers).
DOLFIN I/O was based around XML formats, with memory scalability achieved using SAX parsing (line-by-line read) for input, and using VTK XML output for post-processing, which uses a one-file-per-process (and per time step) model. Issues with these approaches include:
The execution of very large simulations often requires distributed mesh refinement since one is usually limited in the size of mesh that can be generated by the available mesh generation tools. For problems with domain boundaries that can be represented by a `coarse' input mesh, distributed refinement can be used to scalably create a refined mesh for simulation. DOLFIN had support for serial mesh refinement, but no support for the distributed refinement of distributed meshes. The objective of this work package was to develop and implement distributed refinement in two and three dimensions.
Modern HPC systems have an increasing number of processor cores per compute node, and in cases decreasing memory per core. With modern MPI libraries, it can be possible to get very good intra-node parallel scaling for many finite element operations. However, for high core counts and low memory per core the memory overhead for MPI processes can become problematic. Moreover, for some linear solvers, such as direct LU solvers, hybrid MPI/threaded performance in time and memory usage can be dramatically better than pure MPI implementations (e.g., PaStiX [4]). To map the entire solution process (matrix/vector assembly and linear solvers) onto distributed systems with multiple cores per node it is desirable to support hybrid MPI/threaded assembly. There are other benefits to threaded computation on nodes or sockets, such as reduced demands on, and improved matching to, network and disk I/O resources.
The parallel linear algebra libraries supported by DOLFIN include PETSc and Epetra. These libraries provide some support for threaded linear algebra operations (features are rapidly evolving), but are not thread-safe for matrix and vector element insertion. Existing support in DOLFIN for a pure OpenMP approach to assembly is based on:
Profiling and testing focused on a single node of a dual socket system. Detailed profiling was performed to gauge the influence of various aspects of a problem. It became evident that the performance of threaded assembly is more dependent on many more problem/system details than an MPI version, such as architecture, compiler, mesh ordering, degree of freedom map ordering and profiling noise.
Two hardware/compiler systems were used for testing:
Unless otherwise stated, the default DOLFIN Cuthill-McKee degree-of-freedom reordering is applied for spatial locality in the linear algebra objects. This usually speeds up the linear solver phase, but it has been observed in this project that for the DOLFIN unit meshes (square and cube domains) it can lead to a drop in assembly performance since the degree-of-freedom map, while providing spatial locality for the linear algebra objects, no longer maps well onto the order in which the mesh cells are iterated over.
In this project, we have chosen to work with the PETSc linear algebra backend. With a pre-allocated sparsity structure, insertion of on-process matrix/vector entries is thread safe if an entry is not written to simultaneously by more than one thread. Thread safety in this respect is guaranteed by the colouring approach. Insertion of off-process entries in a PETSc distributed matrix or vector is not thread-safe due to the PETSc dynamic caching of these entries. To remedy this, management of caching of off-process entries has been implemented in the DOLFIN interface to PETSc. The layout of the cache is created at matrix initialisation, and off-process entries (the number of which is relatively small) are communicated at the end of the assembly loop, outside of the threaded region.
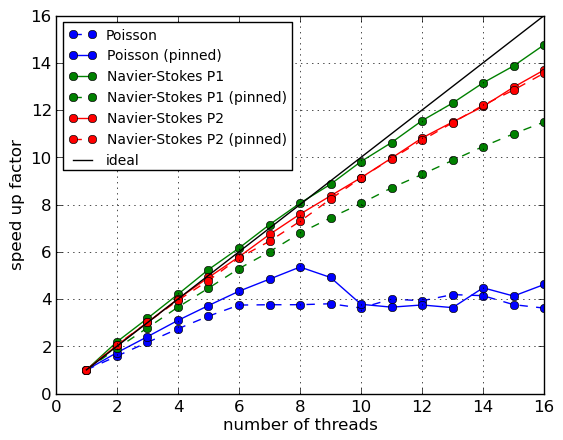
The performance of the colouring approach with a single MPI process on a dual socket node (16 cores) had been tested for a three-dimensional Poisson problem (linear Lagrange elements) and two three-dimensional Navier-Stokes-like problems (linear and quadratic Lagrange elements). The three cases represent a range of scenarios; the Poisson problem has a very compute-light element kernel, and the quadratic Navier-Stokes kernel is very compute heavy. In all cases, the element kernel is generated using the form compiler FFC [6,5] using optimisations. With the highly optimised kernels, the Poisson kernel code requires 58 multiply-add pairs, the linear Navier-Stokes-like kernel around 7.5k operations and the quadratic Navier-Stokes-like kernel around 360k operations. The computational cost of the kernel for the Poisson problem is negligible compared to other operations, such as matrix insertion. At the other extreme, the quadratic Navier-Stokes computation is dominated by the element kernel cost.
The computed speed-up factors using the coloured assembly approach on the Sandy Bridge node are shown in Figure 1.
 |
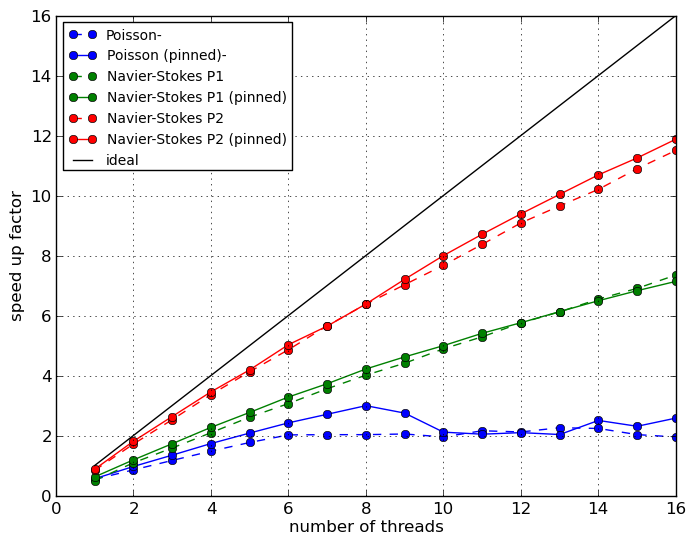
It turns out that Figure 1 is incredibly misleading (as scaling results often can be). The speed-up is presented relative to a single thread version of the colouring assembler, and thereby hides the most important performance measure - runtime. What Figure 1 masks is that the simple colouring approach adopted is fundamentally cache-unfriendly; by construction, it involves operations on data that are not spatially local (to avoid race conditions). If the scaling data presented in Figure 1 is normalised with reference to the default DOLFIN assembler, the picture is very different, and is shown in Figure 2.
 |
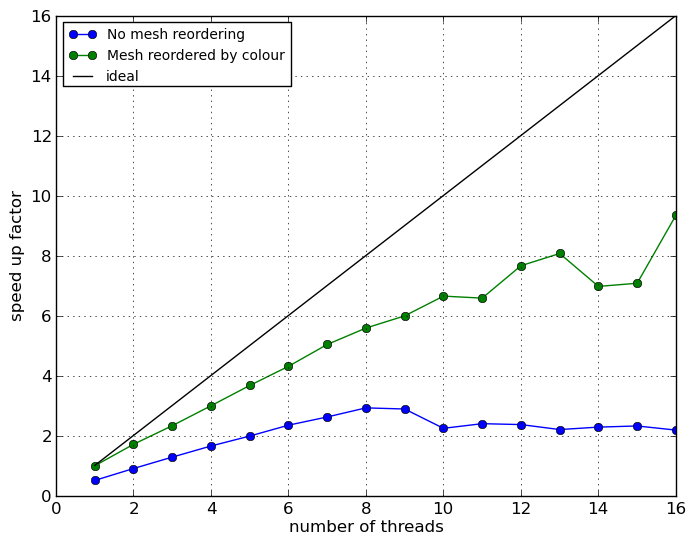
Previous scaling results had indicated that mesh cell re-ordering by colour could enhance scaling for threaded assembly. For the Poisson problem, scaling results with the mesh re-ordered by colour (cells of the same colour are stored in contiguous parts of the array holding cell vertex indices) are shown in Figure 3.
 |
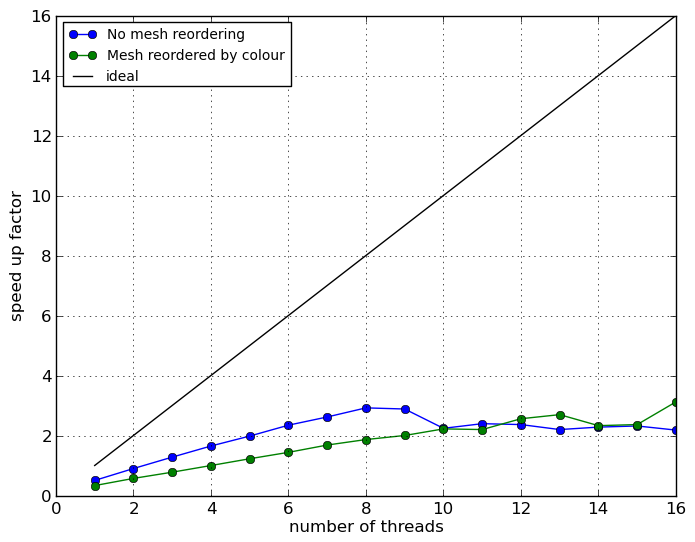 |
The tests with re-ordered meshes illustrate that good speed-ups can be achieved relative to a cache/memory inefficient single threaded assembler, but speed-ups are poor with respect to a cache-friendly assembler. Re-ordering for the coloured assembler does not help as the essence of colouring involves operations of data that are not local. An objective of this work package was to enable mesh re-ordering for distributed meshes akin to that already available for serial meshes. The necessary code infrastructure for re-ordering distributed meshes has been implemented, but the re-ordering strategy advocated in the proposal has not been pursued as performance profiling shows that it is not competitive with MPI-based assembly (by a factor of approximately three with 16 processes).
To handle NUMA effects on dual-socket nodes, it was advocated in the proposal to use one MPI process per socket on a node. For the Poisson matrix assembly problem, the parallel efficiency (normalised by the single thread time and the number of threads) is shown in Figure 5. In the case of the MPI test, the fewest number of threads is two, hence the MPI factor is normalised by the time for two threads. Figure 5 presents results for a Sandy Bridge and a Westmere node.
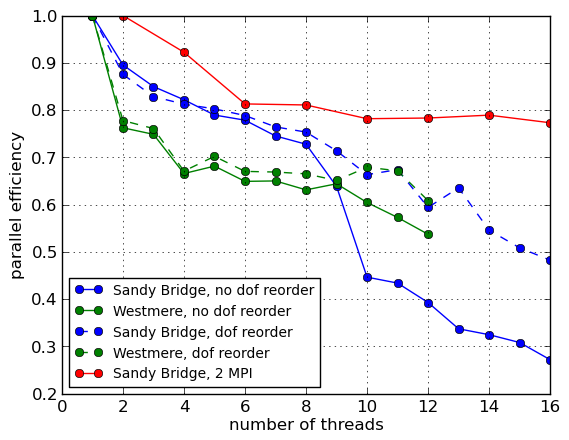 |
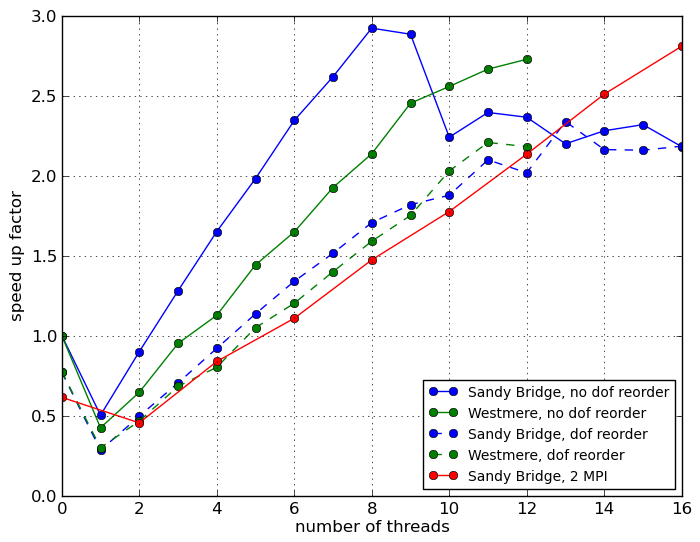
The same results are now presented in Figure 6 as the speed-up factor over the best single threaded performance on the given architecture, which is the standard DOLFIN assembler without degree of freedom re-ordering. Firstly, it shows that not re-ordering the degrees of freedom for this problem does have an impact on performance, bearing in mind however that the performance is still very far from optimal. Secondly, the Sandy Bridge/Intel results appear much more sensitive to ordering than the Westmere/GCC node. Thirdly, only the hybrid OpenMP/MPI case exhibits linear scaling across the range of threads, and it is the fastest when using all available cores, although slower than the default MPI assembler by a factor of three for 16 processes.
 |
Support for hybrid OpenMP/MPI assembly has been implemented, as planned. In terms of scaling, running two MPI processes on a dual socket node appears to overcome the NUMA effects observed for a pure OpenMP approach with a lightweight element kernel when spanning CPU sockets. However, it became clear that the advocated form of the colouring approach is fundamentally cache-unfriendly and the required algorithmic change incurs a large overhead with just one thread compared to the non-coloured version of the assembler with good ordering. For a problem with otherwise good data locality, the straightforward cell colouring approach is therefore not recommended for threaded assembly. The profiling and testing performed during this project has suggest some alternative thread-safe schemes that will have improved data locality and which will be investigated in the future, building on the developments of this project.
The necessary code re-factoring and development to support mesh re-ordering with distributed meshes has been merged into the DOLFIN master development repository. It will form the basis for future investigations into new threaded assembly strategies. The hybrid assembly code is available in a separate repository from the master branch, but due to the observed performance issues it will not be merged immediately into the master branch.
Before this project, most I/O in DOLFIN was either in DOLFIN XML or VTK XML formats. Whilst these are simple and work well for small datasets on serial machines, they are difficult to use in parallel. XML is a text format, and reading in parallel requires every process to read the entire file and parse it. Writing often involves gathering all data on one node, or, in the case of VTK XML output, producing a new file at each output on each process. Therefore, with a highly parallel, time-dependent problem, hundreds of thousands of files could be produced. VTK is primarily a visualisation format, and cannot be read back into DOLFIN (VTK read is not supported as it is not a lossless format).
HDF5 was chosen as a library on which to build parallel DOLFIN I/O. HDF5 is portable, actively developed, well supported and widely available library with parallel I/O via MPI-IO and support for parallel systems. The API is well documented (see http://www.hdfgroup.org) and it provides a flexible, hierarchical internal structure for files, which looks like a file system made up of groups and datasets. HDF5 adopts a single binary file approach in parallel, with each process writing to a defined part of a file.
Whilst HDF5 offers great flexibility, it does not provide any defined formats for data files for use with third-party visualisation tools. Therefore, it was it was decided early in the project that a scalable visualisation format would be highly desirable. After some investigation, XDMF (see http://www.xdmf.org) was chosen. Lightweight meta-data for XDMF files is written in XML, with `heavy' problem data stored using HDF5. XDMF files can be read by widely used visualisation tools, including ParaView (http://www.paraview.org) and VisIt (https://wci.llnl.gov/codes/visit/home.html).
With these choices, there is a clear upgrade path in parallel for users from XML to HDF5 and from VTK to XDMF.
Figure 7 shows the time taken to read a mesh with 34M cells from file on an eight-core workstation using the existing DOLFIN XML parsing and the new HDF5 functionality. A speed up factor of over 100 is already apparent at this scale, and is even more stark on HPC architectures.
Figure 8 shows timing for reading a mesh with 34M cells (1.3GB) on three different systems (University of Cambridge system Darwin, HECToR and Bullard at the Department of Earth Sciences, University of Cambridge). The time taken to read the mesh is generally independent of the number of processes, although there is a certain amount of noise in the results, probably due to file caching and filesystem variability. It is nearly always under 10s, which in the context of the solution runtime on such a mesh is negligible. Note that the time to partition the mesh amongst the processes using the SCOTCH library is significantly greater than the time spent reading the mesh from file.
Writing a mesh to file is more time consuming than reading, as it is necessary to sort the mesh vertices into order before writing. Because the mesh is distributed, some vertices appear on more than one process. Moreover, the XDMF format implicitly assigns global indices to vertices based on position in the file. In order to simplify the file to be written to disk, the duplicates are eliminated by sorting them into order first. Figure 9 shows the timings for writing a tetrahedral mesh of a cube with 100 vertices in each direction on the three different systems. Again, the timings are fairly flat for the write operation, and generally 10s or under on Darwin, 20s on HECToR and 200s on Bullard. The Bullard cluster uses Ethernet and NFS entirely for communication and storage, respectively, so is therefore significantly slower at writing than the other systems.
Finally, we consider DOLFIN Function input and output. A Function can be considered as a collection of data organised on a mesh according to a degree of freedom map. The degree of freedom map gives the relationship between the data and the mesh entities. Because the data is in no certain order when distributed amongst processes, this poses the biggest challenge, since when reading the Function back in, it may be on a different number of processes. In this case, the new degree of freedom map will be ordered differently from the degree of freedom map in the file, and considerable sorting has to be done. In all, seven MPI all-to-all sequences are required to reorder the data correctly. Figure 10 shows the results on the different architectures. Here we consider a 48M cell cube. The scaling properties are generally satisfactory, and again here, the slow speed of I/O on the Bullard cluster can be noticed.
The original I/O objectives were achieved. In addition, support for a new visualisation format with improved performance has been implemented. DOLFIN now has a well defined interface to the HDF5 library, enabling all the functionality which was described in the original design proposal. Additionally, support for a metadata format called XDMF has been implemented, which allows many of the HDF5 output formats to be read by widely available visualisation software. Given the very large performance gain over existing XML formats and the observation that I/O time did not increase for a fixed size problem with increasing with process count on modern systems, there was no need for data aggregation in practice, as suggested in the proposal. For the range of process counts considered, we would expect the cost of data aggregation to outweigh any benefits. Moreover, the use of threaded assembly on compute nodes will effectively provide node-level aggregation. The code developed has dramatically improved performance for parallel I/O and provided a framework for future work in this area.
The supported file formats that are available for different objects in
DOLFIN, following this project, are summarised in
Table 1. The necessary code is either already
included in the most recent DOLFIN release or in the master
development branch for the next release.
Two interfaces were developed for mesh refinement in parallel, one for two-dimensional meshes, and one for three-dimensional meshes. Although they share some commonalities, the algorithms are quite different in two and three dimensions. In both cases, a common class was used to store information about shared facets. An edge bisection method was used for refinement, which required a simple round of MPI communication to pass the bisection information between processes, eliminating the need for a new `distributed mesh query manager'.
In two dimensions, an algorithm from Carstensen [7] was implemented, which preserves the similarity shapes of the triangles being refined. In three dimensions, it is not possible to maintain the similarity shapes so easily, and the quality of the mesh is not guaranteed. For future work, it will be necessary to put markers on cells that are not fully refined, and use these for determining the behaviour of multiple further refinements. Marker-based refinement was implemented, and has enabled existing mesh adaptive solvers to now work in parallel.
Beyond the scope of the original proposal, some simple load balancing has been possible. By calling the mesh partitioner after each level of refinement, the mesh can naturally divide between processes according to the number of cells. Work was put into the interfaces to ParMETIS and Zoltan to make this more efficient.
To compare the efficiency of mesh refinement on different architectures, the time taken to refine a 6M cell tetrahedral mesh mesh of a cube to 48M cells was measured with different numbers of processes. As can be seen from Figure 11, scaling varied somewhat between architectures, with Darwin again performing best. Apart from one anomalous case, the refinement took less than 10 seconds on all machines.
The objectives of the project for distributed mesh refinement have been achieved and exceeded. Beyond the scope of the proposed work, load balancing for refined meshes has been implemented. The developed code has been merged into the DOLFIN master branch and will be part of the next release.
The functionality developed in this project is available to the many users of the FEniCS libraries around the world. The FEniCS Project is an open-source project, and as such, is freely available to download from the Internet. The developments in this project have been announced via FEniCS mailing lists as they became available during the project.
All source code developed in this project is hosted at https://bitbucket.org/chris_richardson/nag-dcse. Much of the code is available in the most recent release of DOLFIN or has been merged into the master development branch of DOLFIN, at http://www.bitbucket.org/fenics-project/DOLFIN, and will be included in the next release of DOLFIN.
The objectives set out in the proposal for this project have all been achieved. The developed software is publicly available, and in most cases will appear in the next release of the library DOLFIN. Unit tests have been developed for the functionality developed in this project, hence the new code is covered by the FEniCS automatic testing framework. The parallel I/O functionality developed in this project is already being used in a number of research projects, and in this context has enabled new investigations that were not previously possible due to parallel I/O limitations.
In addition to the objectives in the project proposal, the efficiency and scalability of building distributed graphs for mesh partitioning has been improved substantially, and load balancing for distributed meshes has been implemented.
This project was funded under the HECToR Distributed Computational Science and Engineering (CSE) Service operated by NAG Ltd. HECToR - A Research Councils UK High End Computing Service - is the UK's national supercomputing service, managed by EPSRC on behalf of the participating Research Councils. Its mission is to support capability science and engineering in UK academia. The HECToR supercomputers are managed by UoE HPCx Ltd and the CSE Support Service is provided by NAG Ltd. http://www.hector.ac.uk