This report documents the work performed during the dCSE
project titled Improving the scaling
and performance of GROMACS on HECToR using single-sided communications.
The project has been undertaken at EPCC, The University of Edinburgh, in
conjunction with Professor Berk Hess, from the KTH Royal Institute of
Technology, Stockholm, and Dr Andrew Turner and Dr Ruyman Reyes from EPCC,
University of Edinburgh.
The project attempted to reduce the computational resources
required to undertake scientific simulations, enabling more efficient use of
the resources provided by the HECToR service (and other HPC systems), and
reducing the runtime required to undertake simulations for large scale
problems.
GROMACS[1] is a versatile package to perform molecular
dynamics, i.e. simulate the Newtonian equations of motion for systems with
hundreds to millions of particles.
It is primarily
designed for biochemical molecules like proteins, lipids and nucleic acids that
have a lot of complicated bonded interactions, but since GROMACS is extremely
fast at calculating the non-bonded interactions (that usually dominate
simulations) many groups are also using it for research on non-biological
systems, e.g. polymers.
GROMACS supports
all the usual algorithms a user would expect from a modern molecular dynamics
implementation.
It also features
high performance compared to all other programs. Since in GROMACS 4.6, the
innermost loops are written in C using intrinsic functions that the compiler
transforms to SIMD machine instructions, to utilize the available
instruction-level parallelism. These kernels are available in both single
and double precision, and are supported by all the different kinds of SIMD
support found in x86-family processors available in January 2013.
GROMACS also
supports CUDA-based GPU acceleration using NVIDIA devices.
The parallel implementation uses MPI and OpenMP to scale up to thousands of
cores.
HECToR[2] (HECToR), a Cray XE6 computer, is the UK National
Supercomputing Service. This project utilised
the Phase 3 incarnation of the system. Phase
3 of HECToR consists of 2816 nodes, each containing two 16-core 2.3 GHz
Interlagos AMD Opteron processors per node, giving a total of 32 cores per
node, with 1 GB of memory per core. This configuration provides a machine with
90,112 cores in total, 90TB of main memory, and a peak performance of over 800 TFlop/s.
Two different test
cases have been used for benchmarking the GROMACS simulation package.
The first test case used in this study is solvated alcohol
dehydrogenase (ADH) in a cubic unit cell (134,000 atoms in total). This system
has issues with load balancing.
The second test case used in this study is a water/ethanol
mixture (Grappa). This test case is available in three sizes and shows good
load balancing, as the system is very homogeneous.
In addition to the performance benchmarks mentioned, we have
made extensive use of the GROMACS test suite, with various combinations of threads
and ranks, to ensure correctness of the code at every stage.
We aim to improve the performance of the inter-task
communications of GROMACS by replacing the calls to standard MPI two-sided
communication routines with a single-sided communication interface which can be
implemented using different single-sided communication libraries (for example,
SHMEM, Fujitsu Tofu interconnect, Infiniband verbs). On HECToR we will
implement the interface using calls to the single-sided, Cray SHMEM communication
routines. SHMEM has been selected as it is currently available in a form that
can give excellent performance on Cray MPP machines (such as HECToR) and is
also currently an area of active development through the OpenSHMEM[3]
initiative. OpenSHMEM currently have a number of reference implementations but
no high-performance versions of their libraries.
For the remainder of this report we will first provide an
initial performance analysis and benchmarking of GROMACS and SHMEM in Section 2.
We will provide implementation details in Section 3, with a description of each
one of the implemented changes. Then, in Section 4 we analyse the performance
of the implementation, showing profiling results and final benchmarking results
for the provided test cases.
To conclude, conclusions and final remarks are provided in
Section 5.
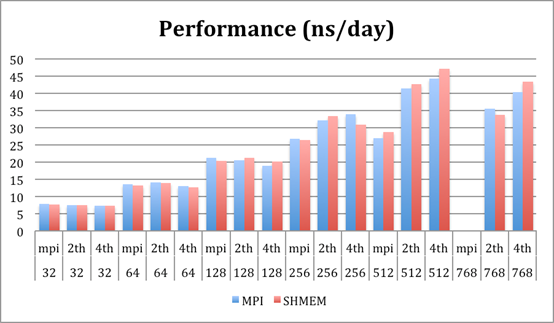
Our initial benchmarking is based on the ADH Cubic test case
supplied by the GROMACS developers using both pure MPI and hybrid MPI+OpenMP (with
multiple OpenMP threads per MPI task). The performance as a function of number
of HECToR nodes is shown in Figure 1.
Figure 1: Performance of GROMACS on HECToR
Phase 3 for ADH Cubic test case using automatic PME load balancing.
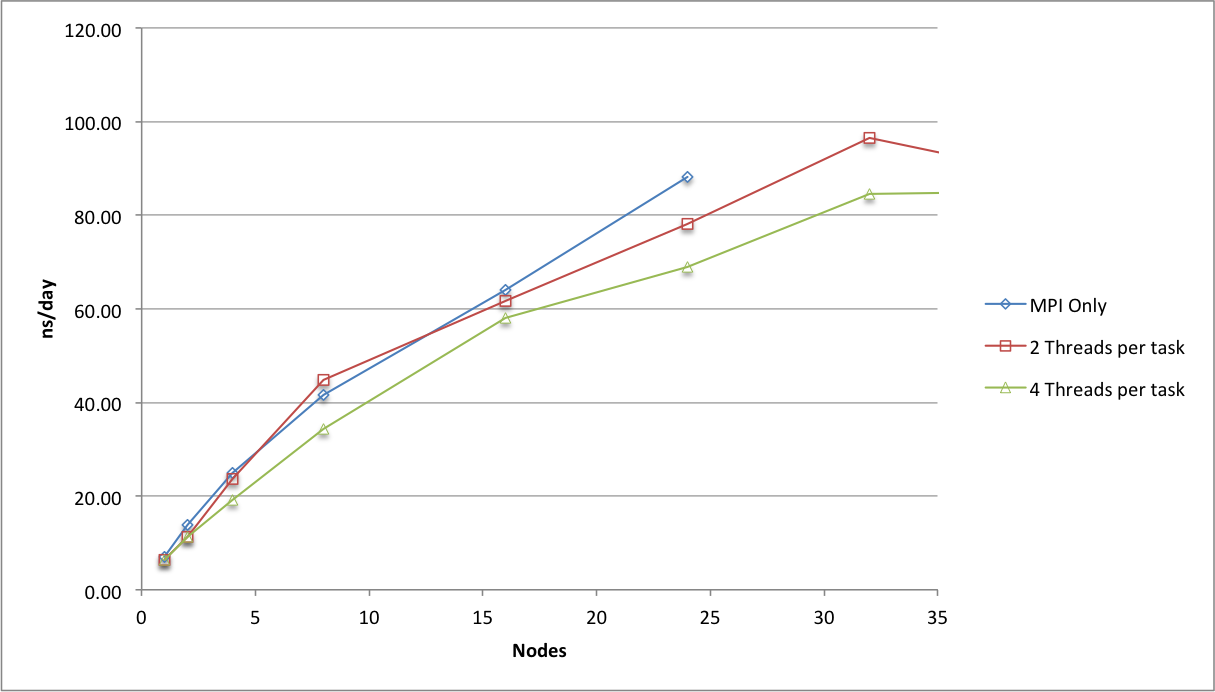
The data shows that the pure
MPI version of GROMACS scales well up to 24 nodes (768 tasks) for this
benchmark. The hybrid version with two OpenMP threads per MPI task generally
shows lower absolute performance but is able to exploit more cores (up to 32
nodes, 1024 tasks). Using higher numbers of MPI tasks for this benchmark is
problematic due to issues matching the parallel domain decomposition to the
larger task count.
The current GROMACS code has been profiled using CrayPAT[4] while running the ADH Cubic benchmark for a
variety of core counts. We have used tracing experiments to profile the code
and gather MPI message statistics.
Table
1
provides an overview of where time in the code is spent when using both 64 and
512 MPI tasks. We can see that, as expected, when we increase the number of
tasks, the MPI communications become a significant portion of the calculation.
In particular, the MPI point-to-point routines (MPI_Sendrecv and MPI_Recv) take
up the majority of the communication time.
Table
1: Sampling results for GROMACS 4.6.0
on HECToR Phase 3 running the ADH Cubic test case. % values indicate average
amount of time spent in named routine.
|
Function
|
64 MPI Tasks
|
512 MPI Tasks
|
|
USER
|
76.7%
|
49.1%
|
|
Main
|
76.7%
|
49.1%
|
|
MPI
|
22.5%
|
47.4%
|
|
MPI_Recv
|
4.6%
|
27.1%
|
|
MPI_Sendrecv
|
6.7%
|
11.3%
|
|
MPI_Alltoall
|
1.2%
|
5.0%
|
|
MPI_Waitall
|
9.6%
|
2.9%
|
|
MPI SYNC
|
0.8%
|
3.5%
|
|
MPI_Alltoall
|
-
|
1.5%
|
|
MPI_Bcast
|
-
|
1.5%
|
|
SYSTEM ROUTINES
|
0.0%
|
0.0%
|
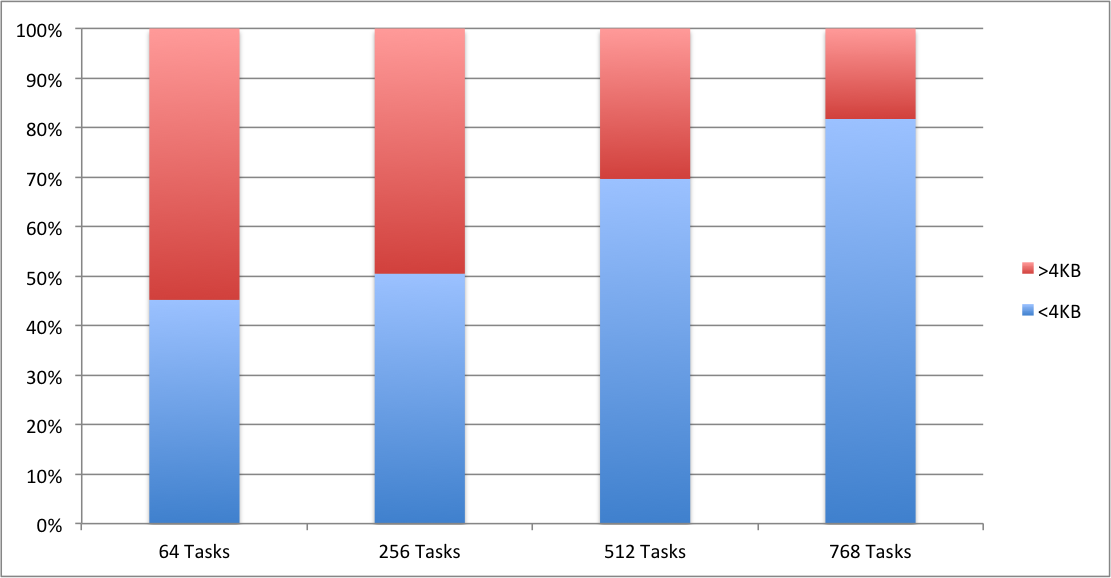
Figure 2
shows how the message size distribution changes for the MPI_Sendrecv routine as
a function of number of MPI tasks. At 512 MPI tasks 70% of the messages are
small (<4KB) and at 768 tasks this share has increased to over 80%.
Figure 2: Distribution of MPI_Sendrecv
message sizes as a function of number of MPI tasks for the ADH Cubic benchmark
in a pure MPI calculation.
This work focused on improving the performance of the
inter-process communication using SHMEM. The implementation details are
described in the following subsections. The majority of the effort invested in
the implementation has been devoted to circumvent the considerations listed
below without breaking the overall GROMACS modularity.
To integrate the SHMEM implementation with the ongoing GROMACS
development, we forked the 4.6.3 release of the package repository and created
a new public development branch with the integrated SHMEM improvements.
A build-time option has been added to the GROMACS CMake
which enables the experimental SHMEM support (GMX_SHMEM). This option tests for
the existence of either Cray or OpenSHMEM support in the platform, and enables
the appropriate macro definitions if it is found. Although the performance
figures shown in this report are based on the Cray SHMEM implementation, the
code can be built in platforms using the OpenSHMEM implementation.
The logically shared, distributed memory access (SHMEM)
routines provide low-latency, high-bandwidth communication for massively
parallel programs.
Applications implemented in SHMEM follow the Single Program Multiple Data
(SPMD) model, hence, no process can be added or removed from the group, and all
processes execute the same application.
This contrasts with the GROMACS approach of using MPMD to
solve the Particle-Mesh-Ewald method (PME) on a predetermined subset of nodes.
To facilitate the work, we have disabled this feature in the command line and
we assume that all nodes perform the PME (-npme
0).
This may hinder performance at larger node counts, limiting
the scaling to the performance of the AlltoAll routine.
Although it would be possible to modify GROMACS so that all
nodes compute PP but only a subset of them will compute the PME, the
development effort required would exceed the time allocated for this
project. Some ideas on how to modify the
GROMACS source to allow the usage of PP and a subset of PME are provided in the
Appendix A.
Another consideration for using SHMEM is the requirement of
using symmetric memory for all the inter-process communication routines.
Symmetric memory is allocated using special routines (shmalloc, shrealloc and shfree). This requires identifying all
the possible allocations of the variables involved in communications and
replacing them with their symmetric counterparts.
In addition, the symmetric memory routines contain an
implicit global barrier, thus we had to ensure that these allocations were
performed simultaneously (and with the same size) across all ranks.
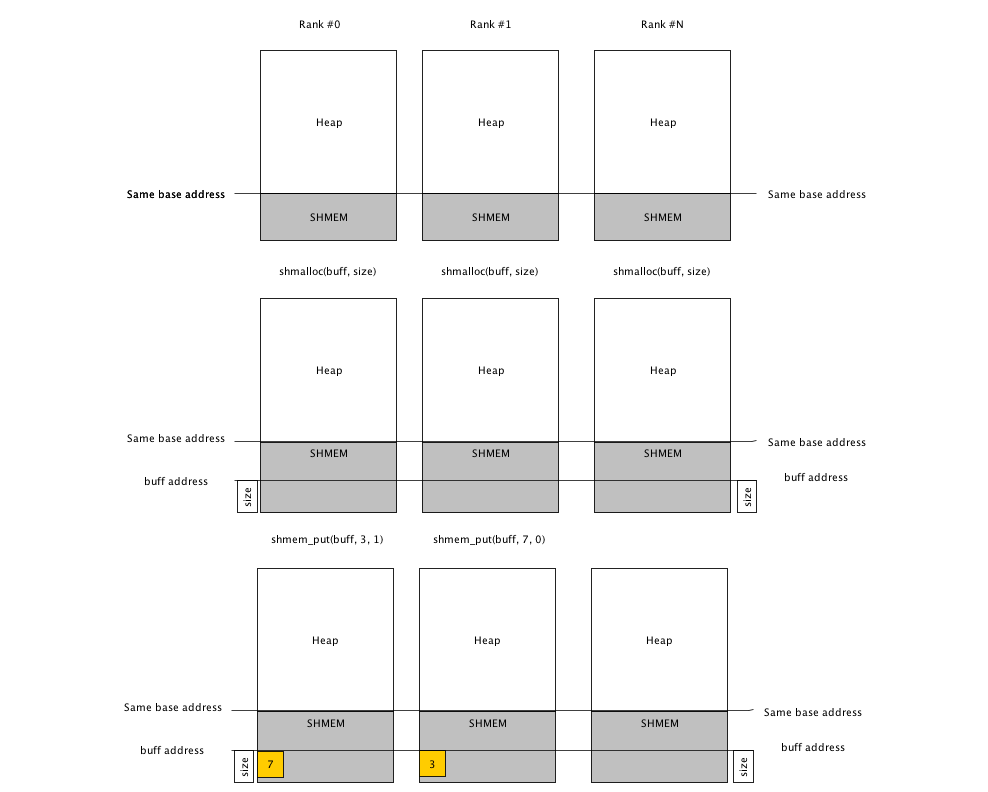
Figure 3 Memory layout of a SHMEM program. Notice that the Symmetric Heap (SHMEM
in the figure) has the same starting base address in all ranks. When a
symmetric allocation routine is called in all PEs, the heap grows
symmetrically. Since the pointer to buff is the same, put/get routines can put
data using the same address in all ranks.
To allocate symmetric memory within GROMACS, we have added
symmetric variants of the already existing routines (snew, srenew, smalloc, srealloc, sfree). The equivalents of these
routines have an extra sh_ before the
name (sh_snew, sh_srenew, sh_smalloc,
sh_sfree). Note that allocation routines do not check if the allocated size
across all ranks is the same.
The macro shrenew
has been created for convenience, and uses the shmem_get_max_alloc routine to compute the maximum amount of memory
requested across all ranks. The shmem_get_max_alloc
routine swaps two synchronization arrays (one for odd, other for even calls) to
allow consecutive calls to the maximum routine without extra synchronization
costs.
void * sh_renew_buf(gmx_domdec_shmem_buf_t
* shmem, void * buf, int * alloc, const int new_size, const
int elem_size)
{
void * p;
int global_max;
global_max
= shmem_get_max_alloc(shmem, new_size);
if (global_max > (*alloc))
{
(*alloc)
= over_alloc_shmem(global_max);
sh_srenew(buf,
(*alloc) * elem_size);
}
p = buf;
return p;
}
SHMEM offers support for both Put and Get one-sided
operations. Put is typically much faster than Get, and we have made our best
effort to use Put as much as possible. However, it is important to note that
Put and Get require different arguments on the symmetric heap. Put requires the
pointer to where the data have to be written to be in the symmetric heap,
whereas Get is the pointer to where the data has to be read the one that have
to reside in the symmetric heap.
In some parts of the SHMEM implementation, we have opted to
use Get over Put to reduce the number of symmetric memory allocations and
facilitate synchronization. A good example of this is the implementation of the
PME part of the code.
The Get version of relevant Send Receive routines can be
selected using the GMX_SHMEM_USE_GET macro.
Cray environment provides several tools for performance
analysis, which include support for SHMEM.
However, debugging SHMEM codes is not an easy task. Despite
having access to the Cray comparative debugger, sometimes tracking dangling
pointers has been an exhausting task. Porting
a code to SHMEM, in particular one as large as GROMACS, moving incrementally
memory allocations to the symmetric heap is not an easy task, and prone to
errors. When a symmetric memory pointer is de-allocated with a non-symmetric
routine, there is no immediate error in the free: The symmetric heap just
become inconsistent and may (or may not) produce errors in future allocations.
This complicates debugging, as errors may appear far from the point where the
real problem is.
We have made extensive use of the GROMACS regression tests
with various configurations to ensure the application returns correct results.
A data structure holding all the control information required
to the SHMEM communications has been created. It is detailed below.
typedef struct {
/* These
buffers are used as temporary
interchange space for SHMEM routines */
int
* int_buf;
int
int_alloc;
real * real_buf;
int
real_alloc;
real * rvec_buf;
int
rvec_alloc;
void * byte_buf;
int
byte_alloc;
/* An
event array to synchronize shmem operations */
shmem_flag_t * post_events;
shmem_flag_t * done_events;
/* Array
of locks (i-th is the lock for the i-th pe) */
shmem_flag_t * lock;
/* wkr
and sync arrays for max_alloc routine */
long * max_alloc_pSync1, *
max_alloc_pSync2;
int
* max_alloc_pWrk1, *
max_alloc_pWrk2;
} gmx_domdec_shmem_buf_t;
This structure is initialised the init_shmem routine, and can be freed with the done_shmem routine, following the example of other data structures
inside the code.
The intermediate buffers are not used in the final
implementation, although we keep them in the data structure to facilitate
possible future work.
The max_alloc_{pSync1, pSync2, pWkr1, pWrk2} arrays are used to
synchronize the shmem_int_max_to_all
routine used to synchronize the buffer size for the reallocation.
The data structure is created when the simulation starts,
and it is associated with the communication data structure. It is later
associated with specific DD, PD or PME control data structures to facilitate
access to intermediate pointers.
The first task undergone in this work was to implement the
Send Receive operations used in the Domain Decomposition part of the code with
SHMEM equivalents.
The DD part
uses pulsed communication, which makes the code a bit simpler and reduces the
number of communication calls.
The Domain Decomposition data structure was extended with a
pointer to a SHMEM control data structure, which contains pointers to
synchronization arrays, temporary buffers, locks, and other control structures
used through the program. The structure is initialised when creating the domain
decomposition structure.
The routine dd_sendrecv_{int,real,rvec} were modified so that they use SHMEM
routines instead of MPI when the build-time option is enabled.
Although integer interchange routines are implemented in
SHMEM they do not represent a major advantage on the performance and they are
disabled by default.
This first approach used a temporary symmetric buffer per-data type, to avoid
replacing all the allocations of the code, as shown in the following listing:
void shmem_void_sendrecv(gmx_domdec_shmem_buf_t*
shmem,
void* buf_s, int n_s, int rank_s,
void* buf_r, int n_r, int rank_r)
{
shrenew(shmem,
shmem->{type}_buf, &(shmem->byte_alloc), n_s);
shmem_lock(shmem,
rank_s);
if (n_s) {
shmem_{type}_put(shmem->{type}_buf,
buf_s, n_s, rank_s);
}
shmem_set_post(shmem,
rank_s);
shmem_wait_post(shmem,
_my_pe());
if (n_r) {
memcpy(buf_r,
shmem->{type}_buf, n_r * sizeof(real));
}
shmem_set_done(shmem,
rank_r);
shmem_clear_post(shmem,
_my_pe());
shmem_wait_done(shmem,
_my_pe());
shmem_clear_done(shmem,
_my_pe());
shmem_unlock(shmem,
rank_s);
}
To ensure there is enough space to store the communication
buffer we call our own shrenew
routine, which computes the maximum allocation required across all ranks and
reallocates memory if required.
The sender PE acquires the lock to gain access to the buffer
and put the data on the destination PE. The receiver PE will wait (shmem_wait_post) until the sender sets a
particular flag (shmem_set_post).
Then, the data in the symmetric buffer is copied to the reception buffer. Both
PE can now set an additional flag to ensure reception (set_done, wait_done), and,
finally, unlock the buffer.
Using the initial global barrier ensures synchronization.
The Figure below
depicts the communication pattern for this implementation when interchanging
data in the forward direction.
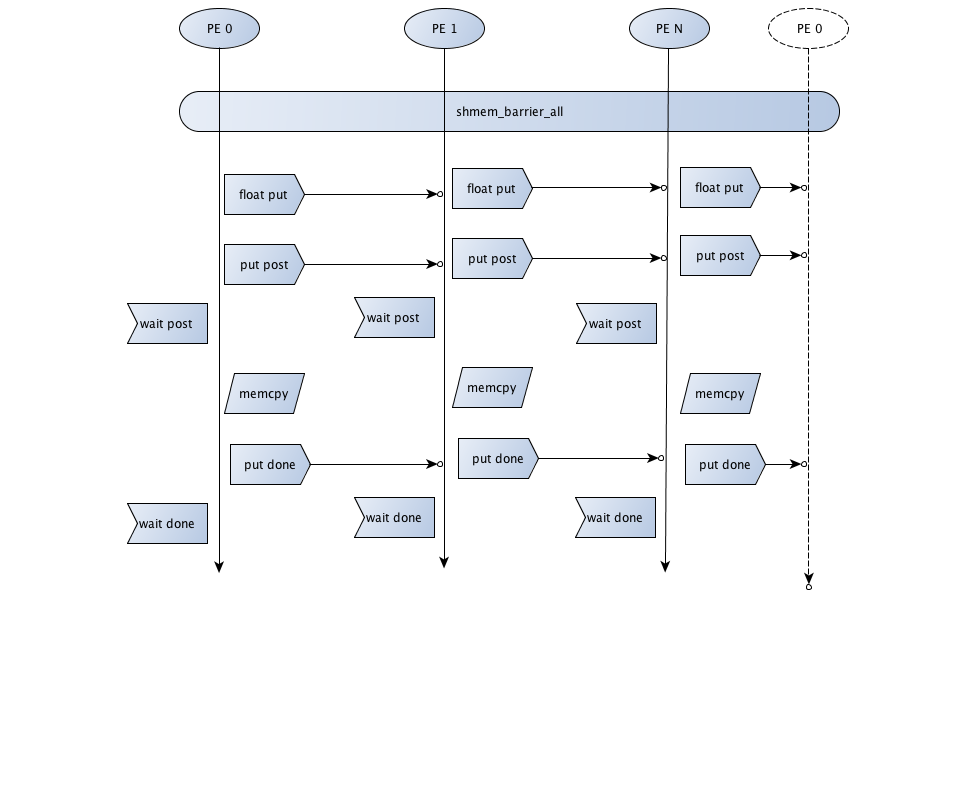
Figure 4 Communication diagram of a
forward pulse. After all PE reach the global barrier, each PE puts data on the forward
node, and then waits to receive data from the backward node.
This approach poses several performance problems. The
obvious one is the requirement of a global barrier to ensure synchronization.
This forces each PE to wait for the rest, hindering performance on unbalanced systems
such as the ADH test case.
Also, the requirement for the receiver to copy data from the
symmetric buffer to the real destination buffer introduces additional overhead,
proportional to the amount of data transmitted.
Due to these restrictions, we moved to Send/Recv routines
without intermediate buffers, therefore modifying the original GROMACS code to
use symmetric allocation routines (see Section 3.3.1).
Our first step to improve the performance of this approach
was to move the memory allocations of those buffers used in the DD
communication to the symmetric heap.
This required, among others, the creation of new init_state and done_state routines implemented the aforementioned symmetric
allocation.
The coordinates and velocities (x and v vectors) of the
state have been ported to symmetric memory, as they are communicated within dd_move_f and dd_move_x routines.
Most of the data structures used in communications are
allocated as follows:
if (local_buffer_size <
number_of_elements * size)
{
local_buffer_size = number_of_elements * size;
buffer =
realloc(buffer, local_buffer_size);
}
Since the number of elements across all ranks is not
constant, the size of the local buffer in the MPI version is reallocated only
on those ranks requiring it. This is not possible on the SHMEM, as it will
produce (a) deadlocks if not all processors need to reallocate and (b) incorrect
symmetric addresses if the size is not the same in all ranks.
To avoid these problems, we re-implement the reallocation
computing the global maximum of the buffer required and reallocating the same
amount in all ranks.
int max = shmem_get_max_alloc(dd->shmem, local_buffer_size);
shrealloc(buffer, max);
Note that the reallocation routine contains a global
barrier.
To avoid the constant reallocation of buffers in the domain
decomposition, we try to move buffer reallocations outside loops when possible,
and work with temporary buffers in the heap if not.
For those buffers whose size depends either on the total
number of charges or the total number of atoms, we pre-compute the maximum
number of charges and atoms per rank and reuse this value whenever possible,
reducing the total calls to the maximum collective.
The DD control data structure has been extended with a
variable that keeps track of the maximum number of atoms in a node. This
variable is updated when nat_home changes, and its value reused in many places to reduce the
calls to the max_to_all collective.
Some of the Send Receive operations used within the domain
decomposition involved sending data from a buffer and receiving there on a
different one. This can be a problem when using one-sided communications. Lets
take the following simple MPI example. First, we communicate the size of the
buffer. Then we do the same with the buffer, according from the data received
before.
Note that the position in the receiver changes depending on
the received information, and that the sender does not now where the data is
going to be written in the receiver.
for (int i = 0; i < nelems; i++)
{
MPI_SendRecv(to_send, 1, MPI_INT, destination[i], 0,
to_recv, 1, MPI_INT, source[i], 0,
MPI_COMM_WORLD, &stat);
MPI_SendRecv(buf[i], to_send, MPI_INT, destination[i], 0,
rec[pos], to_recv, MPI_INT, source[i], 0,
MPI_COMM_WORLD, &stat);
pos +=
to_recv;
}
If we port these Send Receive operations by simply writing
the information from the sender to the receiver (using a put operation with no
intermediate buffer) we will end up with incorrect results, as the position
where the sender is writing does not necessarily match the position the
receiver is expecting.
To overcome this problem, the Sender needs to know where the
offset in the receiver to put the data. In our implementation, the receiver
puts the offset on the sender, and then waits for the data to be sent.
However, it is required to change the signature of the dd_sendrecv_{rvec,real,int}
functions, so that the offset to the symmetric buffer can be differentiated
from the pointer address itself. New dd_sendrecv_{rvec,real,int}_off have been created for that purpose.
The code shown below illustrates the interchange of sizes and offset that
happens before sending the data.
if ( recv_size > 0 )
{
/*
Receiver: Put offset on sender */
shmem_int_p(&rem_off,
off_r, recv_nodeid);
/*
Receiver: Put size on sender */
shmem_int_p(&rem_size,
recv_bufsize, recv_nodeid);
/*
Receiver: Ensure delivery (but not reception!) */
shmem_fence();
}
if ( send_size > 0 )
{
/*
Sender: Wait for offset from receiver */
shmem_int_wait(&rem_size, -1);
}
Another implementation problem related with the offset
interchange is that sometimes the base pointer where the routine has to put to
or get the data from is not symmetric across all ranks. For example, in some
situations, some ranks will receive the data in place while others need to
receive the data on a temporary buffer.
This problem notably appears in some routines used in the
domain decomposition.
Depending if the implementation uses put or get, which
buffer we are writing to needs to be communicated. The appropriate code can be
enabled with pre-processor directives (USE_GETMEM or USE_PUTMEM macros).
The implementation for the interchange of the x buffer in the dd_move_x routine is outlined below:
static int rparams[2] = { -1,-1 };
static int call = 0;
int tmp[2];
shmem_wait_for_previous_call(dd->shmem,
&call, dd->neighbor[d][0]);
tmp[0] = cd->bInPlace;
tmp[1] = nat_tot;
// First stage: Communicate in place and offset
dd_sendrecv_int_nobuf(dd, d, dddirForward, tmp, 2,
rparams, 2);
{
rvec * rem_rbuf =
rparams[0]?x:comm->vbuf2.v;
// Second stage: Communicate the data
dd_sendrecv_rvec_off(dd, d, dddirBackward,
buf, 0,
ind->nsend[nzone+1],
rem_rbuf,
rparams[0]?rparams[1]:0,
ind->nrecv[nzone+1]);
}
call++;
After ensuring that both receiver and sender are on the same
iteration, we communicate the value of the inPlace
variable and the offset to the Forward direction, so that the senders have the
positions where they have to write data in the next Send Receive operation.
Notice that the sender will use either x
or the temporary buffer to put the data depending on the value received from
the receiver in the previous stage.
Our next step was to eliminate the global barrier before the
each call to the Send Receive operation.
Since in the domain decomposition all PEs call the Send
Receive operations at the same point in the code but not at the same point in
time we can replace the global barrier with a call counter. Whenever a rank calls
a Send Recv operation, it checks the sender and destination values for this
routine counter, and waits until the value match its own. When the Send Recv
operation finishes, it increases the counter.
This mechanism enables two ranks to synchronize without
affecting the rest, thus reducing the overhead on poorly balanced codes. We have
implemented this mechanism as a subroutine (shmem_wait_for_previous_call)
and use it thorough the SHMEM parts of the code as a replacement for barriers
whenever possible.
void shmem_wait_for_previous_call
(gmx_domdec_shmem_buf_t * shmem,
int * call, int rank)
{
while (
(shmem_int_g(call, rank)) != (*call) )
{
sched_yield();
}
}
Using sched_yield
forces the current process to go back to the end of the pending queue. This may
help the Cray MPI progress thread to continue process messages, or other
threads to access to the CPU while waiting which is particularly interesting
for OpenSHMEM implementations.
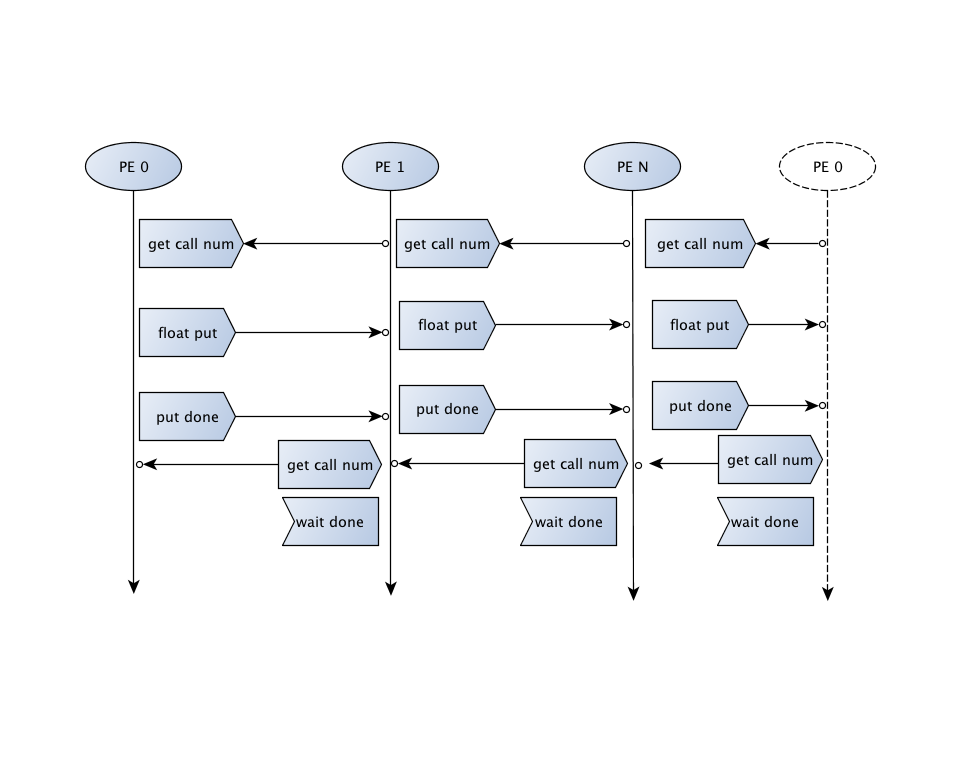
Figure 5 Call diagram of the
optimized Send Receive operation implemented in SHMEM.
For illustrative purposes, Figure above
illustrates the call diagram of the Send Receive operation using N ranks, where
the i-th rank sends data to the i+1%N
rank, and receives from the i-1%N rank. Where possible, the sending/receiver
part of the routine is only executed if there is data to send/receive.
In some situations inside the DD part, it is necessary to
send information in both forward and backward direction. If performed
simultaneously, it provides an important performance benefit. The dd_sendrecv2_rvec routine implements
this operation in MPI making use of non-blocking Send / Receive operations.
We have implemented similar functionality in the new SHMEM
implementation using non-blocking SHMEM put operations to transfer the
information, producing a specific dd_sendrecv2_rvec_off
routine that puts data in both directions simultaneously.
To reduce the impact of the implicit barrier during the
memory re-allocation, we took advantage of the fact that the size of the
communication buffers grows during the initial steps of the simulation, but later
it stabilises around a number. This
enabled us to implement a simple heuristic that detects the number of times the
size of a particular buffer has been changed. If in a certain number of
iterations this size has not changed, we disable the reallocation (and the call
to the global max collective).
In case that at some point after disabling the
re-allocation, the size of the buffer is increased over the last time it was
re-allocated, the code stops the simulation with a descriptive message.
Developers can modify the value of the MAX_SAME macro to set
the number of times the reallocation is called with the same size before
disabling it. The listing below shows an example of the implementation of this
simple heuristic when reallocating the sate data structures.
{
static int nsame_natoms = 0;
if (nsame_natoms < MAX_SAME)
{
int
max = shmem_get_max_alloc(dd->shmem,
state_local->natoms);
if
(max > state_local->nalloc)
{
dd_realloc_state_shmem(state_local, f,
max);
nsame_natoms = 0;
}
else
{
nsame_natoms++;
}
}
else
{
if
(state_local->natoms > state_local->nalloc)
{
gmx_fatal(FARGS, " New natoms value
greater
than old_natoms, increase
MAX_SAME \n");
}
}
}
The particle decomposition (PD) part of the code is relatively
simpler than the DD part, with less number of lines and a simpler communication
pattern. However, since this part of the code may be deprecated in the near
future, we have only focused on correctness and not performance.
In addition to those memory allocations already moved for
the DD part of the code the PD part of the code makes use of temporary buffers
for some communications. These buffers have been moved now to the symmetric
heap. Some refactoring work was required to move the buffer allocations to
ensure all ranks execute the allocation instructions.
For example, in the setup_parallel_vsites
routine, there are several calls to the add_to_vsite_list
routine, which in turns reallocates either the left_import_construct or the right_import_construct. These reallocations will deadlock if not
performed symmetrically.
The SHMEM implementation creates the symmetric buffers after
the aforementioned loop and copies the initial data to this symmetric buffer.
In addition, send and receive buffers - which in the MPI
implementation were allocated to the local size in each rank are allocated to
the maximum size of the buffer across all ranks.
Since the PD part of the code only uses the state_global variable, instead of than
replicating the global state on local states as the DD part of the code does,
the allocation of this global state buffer had to be moved to the symmetric
heap as well.
However, the state_global
structure is used to load data from the input files, a task performed only by
the master node. This implies that the symmetric memory cannot be allocated at
this point.
Although the logically sound point to do this reallocation
would be the set_state_entries
routine, which fixes the state data structure after the file has been
initialised and it is called by all ranks, this breaks the modularity of the
code, due to the fact that all variants of the code (DD, PD, non-pararallel) go
through this routine.
In order to keep the modularity we have modified the partdec_init_local_state routine, which
initialises the state when using PD, so that the existing coordinates and
velocities are moved to the symmetric heap at this point, copying the data from
the global to the local state, rather than reassigning de pointers as the MPI
version does. Since this is in the initialisation phase, we do not expect to
cause major performance problems.
int i;
int max_atoms =
shmem_get_max_alloc(cr->pd->shmem,
state_global->natoms);
sh_snew(state_local->x, max_atoms);
sh_snew(state_local->v, max_atoms);
cr->pd->max_atoms = max_atoms;
if (state_global->natoms)
{
if (state_global->x)
{
for (i = 0; i < state_global->natoms;
i++)
{
copy_rvec(state_global->x[i],
state_local->x[i]);
}
sfree(state_global->x);
state_global->x = state_local->x;
}
Majority of the Send Receive operations use the gmx_tx_rx routine. We have created a set
of type-specific versions of these routines and implemented them using our
previously developed Send Receive routines.
Those situations where offset were involved have been solved
using the same mechanism as in the DD part (_off
variants of the routines).
To optimise the MPI implementation, some movement routines
implemented a deferred send and wait using non-blocking communication, as shown
below, in an attempt to send and receive from both directions at the same time.
start = cgindex[cur];
nr =
cgindex[cur+1] - start;
gmx_tx(cr, GMX_LEFT, cg_cm[start],
nr*sizeof(cg_cm[0]));
start = cgindex[next];
nr =
cgindex[next+1] - start;
gmx_rx(cr, GMX_RIGHT, cg_cm[start],
nr*sizeof(cg_cm[0]));
gmx_tx_wait(cr, GMX_LEFT);
gmx_rx_wait(cr, GMX_RIGHT);
This is not required in the SHMEM implementation, as there
is no need for a receive statement. The SHMEM implementation only calls the
offset version of the gmx_tx_rx
routine, as shown below
int start_s = cgindex[cur];
int nr_s = cgindex[cur+1] - start_s;
int start_r = cgindex[next];
int nr_r = cgindex[next+1] - start_r;
gmx_tx_rx_real_off(cr, GMX_LEFT, *cg_cm, start_s *
DIM, nr_s * DIM,
GMX_RIGHT, *cg_cm, start_r * DIM, nr_r * DIM);
It is worth noting, from the above code snippet, that
pointer arithmetic should be taken into account when using offset routines. The
offset of the memory is based on the size of the datatype. In the snippet,
since the communication routine is of type real and the cg_cm vector is of type rvec
(which is, in turn, a real[NDIM] vector), the offset have to be
adjusted accordingly. This happens also in the move_rvecs routine, where the original code simply used vecs[index[cur ]] but the code using offset interchange
requires a not-so-readable offset of index[cur]
* DIM.
gmx_tx_rx_real_off(cr,
GMX_RIGHT, *(vecs),
index[cur ] * DIM,
HOMENRI(index, cur )*DIM,
GMX_LEFT, *(buf),
index[prev] * DIM,
HOMENRI(index, prev)*DIM);
The final part of this project was focused on the
implementation of the PME part of the code using the SHMEM routines. Due to
time constraints, we focused only on those routines strictly appearing on the
profiling results containing Send/Receive operations.
All communications used in the PME part of the code use a
separate communicator, with routines using this indexing rather than the global
one.
Since there are no subgroup capabilities on SHMEM, we had to
convert the communicator IDs to global IDs, usable by SHMEM routines.
The pme_get_global_id
routine implements that conversion using the MPI_Group_translate_ranks routine, as shown below.
int pme_get_global_id(pme_atomcomm_t
*atc, int nodeid)
{
int
global, ret;
int
group, wgroup;
ret = MPI_Comm_group(atc->mpi_comm,
&group);
if (ret != MPI_SUCCESS)
error check
ret = MPI_Comm_group(MPI_COMM_WORLD,
&wgroup);
error check
ret
= MPI_Group_translate_ranks(group, 1, &nodeid,
wgroup,
&global);
error check
return global;
}
The routine first gets a pointer to both the PME group and
the world group, and then translates the nodeid rank number to the global rank
number.
We have experienced some difficulties with these MPI
routines, producing random crashes when called many times, thus, we try to
minimise its use as much as possible.
Send/Receive operations in the PME part of the code are
encapsulated on calls to the pme_dd_sendrecv
routine. The destination and source nodes for each of these calls are
determined by the shift of the communication, using the node_dest and node_src arrays.
These values are converted to global ranks with the pme_get_global_id routine.
We have reused the SHMEM Send/Receive routines from previous sections to
implement the PME communications.
However, in this case Send/Receive operations are not
necessarily called by all ranks at the same point in the code, since some ranks
may not communicate at a particular shift. Since the shmem_wait_for_previous_call is useless in this situation, other
mechanism has been used.
In addition, Send/Receive operations in the MPI implementation
rely on separate tags for each shift to differentiate messages, which is not
possible in the SHMEM implementation.
The redistribution of coordinates and charges in the PME
part is performed by the dd_pme_redist_x_q
routine. This routine put the charges and forces on to a buffer and then
sends/receive them across all nodes involved in the PME, as shown below.
// Reallocate buffers
// Communicate the count
for (i = 0; i < nnodes_comm; i++)
{
int scount =
atc->count[commnode[i]];
pme_dd_sendrecv(atc, FALSE, i,
&scount, sizeof(int),
&atc->rcount[i],
sizeof(int));
atc->n +=
atc->rcount[i];
}
// Copy data to send buffer
buf_pos = 0;
// Communicate charges and coordinates
for (i = 0; i < nnodes_comm; i++)
{
scount =
atc->count[commnode[i]];
rcount =
atc->rcount[i];
if (scount > 0 || rcount > 0)
{
if (bX)
{
/* Communicate the coordinates */
pme_dd_sendrecv(atc, FALSE, i,
&pme->bufv[buf_pos],
scount*sizeof(rvec),
&atc->x[local_pos], rcount*sizeof(rvec));
}
/*
Communicate the charges */
pme_dd_sendrecv(atc, FALSE, i,
pme->bufr + buf_pos,
scount*sizeof(real),
atc->q + local_pos,
rcount*sizeof(real));
buf_pos += scount;
local_pos
+= atc->rcount[i];
}
}
Since not all nodes had to communicate in all shifts, and
not all nodes have the same destination and source in all shifts, it is
possible that a node that does not communicate in the first shift, has to do it
on the second shift. Since there are no tags in the SHMEM implementation, this
processor may write on the buffer while a node from the previous shift is still
reading data, potentially causing corruption or even deadlocks if the offset or
done flags are incorrectly modified.
To avoid this problem, instead of using the traditional
Send/Receive replacement, we decided to follow a slightly different approach
this time, and modify the redistribution routine itself rather than the
low-level one.
The SHMEM implementation is depicted below. The main idea is
that, since we are using one-sided communications, we do not need to
communicate the buffer sizes, we only need to put the
data in the proper place.
In this case we had two options: Either the sender ranks
putting data on the appropriate position of the receiver or the receiver
getting data from the correct positions in the sender.
Since using get in this case required only the PME buffers
to be allocated in the symmetric memory we opted in this case to implement the
routine using get instead of put.
Instead of using Send/Receive to get the value of rcount, we moved the count array to the symmetric heap so the
receiver can get it directly from the sender.
The values of count are computed in the routine pme_calc_pidx_wrapper. We added a recount_call field to the atc structure, so we can ensure that we
are getting data from the correct iteration. We also added an acum_rcount field to the atc structure, which is initialised with
the accumulated values of the count value (i. e a[i] = a[i 1] + count[i],Ρ i > 0 ).
In this alternative implementation of the redistribution,
where the active role is in the receiver side, the sender needs to wait until
the receivers had retrieved the data. The more we can defer this wait, the
better we can hide the cost of the PME communication. Currently we have
implemented this wait at the end of the redistribution routine, but a detailed
study of the code may reveal other approaches.
The wait is implemented using a counter. The static variable
used is initialised with the total count of data that will be retrieved
from the node.
Each receiver uses an atomic operation to decrease this
value in the sender.
The sender will wait until the value of used is zero again
before invalidating the buffer. The ready flag tells acts as a barrier,
ensuring that the receiver can read
the used variable, and the data from the count is array is valid.
This approach allows the receiver to get the data from the
sender completely independent from the sender, once the ready flag is set.
// Reallocate buffers
/* Get the num of elements to receive by this PE */
for (i = 0; i < nnodes_comm; i++)
{
int src
= pme_get_global_id(atc,atc->node_src[i]);
int rcount;
shmem_wait_for_previous_call(atc->shmem,
atc->recount_call,
src);
rcount =
shmem_int_g(&atc->count[atc->nodeid], src);
atc->rcount[i]
= rcount;
atc->n
+= rcount;
}
// Copy data to send buffer
buf_pos = 0;
// Communicate charges and coordinates
for (i = 0; i < nnodes_comm; i++)
{
int src
= pme_get_global_id(atc,atc->node_src[i]);
while (
shmem_int_g(atc->recount_call, src)
!= *(atc->recount_call) )
{
sched_yield();
}
used +=
atc->count[commnode[i]];
}
shmem_int_p(&ready, 1, _my_pe());
shmem_quiet();
for (i = 0; i < nnodes_comm; i++)
{
int scount
= pme_get_global_id(atc, atc->count[commnode[i]]);
int rcount
= pme_get_global_id(atc, atc->rcount[i]);
if (rcount > 0)
{
{
shmem_fence();
while
(!shmem_int_g(&ready, src))
{
sched_yield();
}
}
int
rem_buf_pos = shmem_int_g(&atc->acum_count[i], src);
if
(bX)
{
shmem_getmem(&atc->x[local_pos][0],
&pme->bufv[rem_buf_pos][0],
rcount * sizeof(rvec), src);
}
shmem_float_get(&atc->q[local_pos],
&pme->bufr[rem_buf_pos], rcount, src);
local_pos
+= atc->rcount[i];
shmem_int_add(&used,
(-1) * rcount, src);
}
{
shmem_fence();
// Wait
until all processes have retrieved the data
while ( (volatile) used )
{
sched_yield();
}
//
Invalidate the buffer data
shmem_int_p(&ready, 0, _my_pe());
shmem_quiet();
}
To reduce the amount of time spent waiting for other ranks
to finish, we slightly modified the part where the rcount is computed, so that several
ranks could be checked simultaneously, instead of waiting for a particular one
to finish, which allow us to hide the imbalance in the PME part of the code.
int remaining[nnodes_comm];
int src[nnodes_comm];
int rem_count = nnodes_comm;
int i = 0;
for (i = 0; i < nnodes_comm; i++)
{
remaining[i]
= 1;
src[i] =
pme_get_global_id(atc,atc->node_src[i]);
}
do
{
for (i = 0; i < nnodes_comm; i++ )
{
if (remaining[i] == 1)
{
/* Get the
num of elements to receive by this PE */
int rcount;
if(shmem_int_g(atc->recount_call,
src[i])== *(atc->recount_call) )
{
remaining[i] = 0;
rem_count--;
rcount =
shmem_int_g(&atc->count[atc->nodeid], src[i]);
atc->rcount[i]
= rcount;
atc->n
+= rcount;
}
}
}
} while
(rem_count > 0);
We have made profuse use of the Cray profiler while working
on the implementation in order to focus our development effort in those areas
where its effect would be beneficial. Some partial analysis and outputs are
shown below to illustrate the evolution of the development process.
Our initial implementation of the Send/Recv routines in the
Domain Decomposition part of the code revealed the unfeasibility of using
buffers locals for the Send Receive operations, due to the excessive overhead
of the buffer reallocation and the global barrier.
|
Group
|
% Time
|
Imb. Time %
|
Name
|
|
USER
|
87.8%
|
|
|
|
|
|
|
|
|
SHMEM
|
6.1%
|
|
|
|
|
4.5%
|
56.5%
|
shmem_int_max_all
|
|
|
1.2%
|
8.08%
|
shmem_barrier_all
|
|
|
0.3%
|
2.0%
|
shmem_put
|
|
MPI
|
5.8%
|
|
|
|
|
5.0%
|
47.5%
|
MPI_Sendrecv
|
The profiler results above, using 8 cores of a HECToR node
with only 10000 iterations of the ADH test code, revealed the limitations of
this approach. Notice that, despite only porting part of the domain
decomposition send receive routines, the barrier and maximum are already 5.7%
of the total 6.1% of the time spent in SHMEM routines. Also, we are only using
intra-node communications, where we expect a similar behaviour between SHMEM
and MPI.
After replacing the buffered Send Recv routines by
non-buffered ones, and reducing the number of calls to the maximum collective,
the profiler output looked as follows (obtained with the same conditions than
the previous case)
|
Group
|
% Time
|
Imb. Time %
|
Name
|
|
USER
|
88.1%
|
|
|
|
|
|
|
|
|
SHMEM
|
5.9%
|
|
|
|
|
3.1%
|
64.0%
|
shmem_wait_event
|
|
|
1.4%
|
58.2%
|
shmem_int_wait
|
|
|
0.7%
|
81.3%
|
shmem_int_wait_until
|
|
|
0.4%
|
48.9%
|
shmem_int_max_to_all
|
|
MPI
|
5.8%
|
|
|
|
|
5.0%
|
47.5%
|
MPI_Sendrecv
|
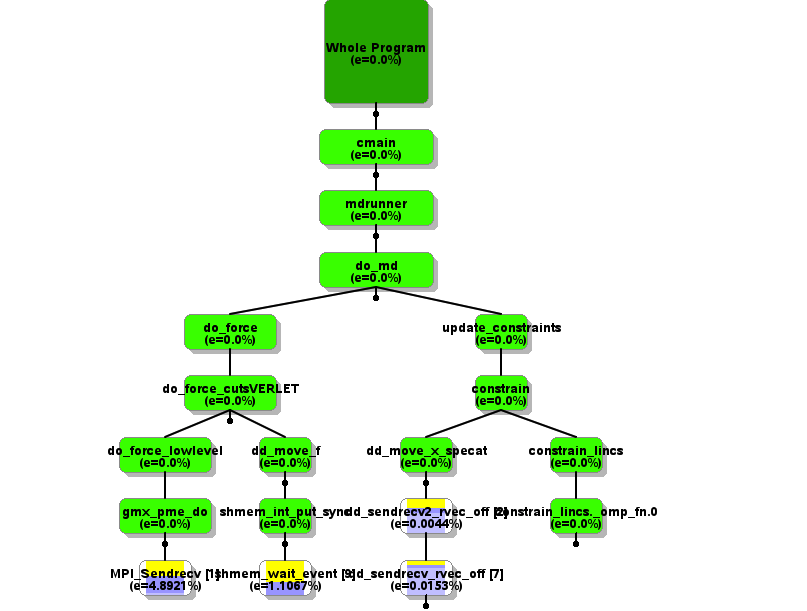
Notice that the maximum collective has nearly disappeared,
and the SHMEM time is spent in the wait_event
routine. The calltree (shown below)
reveals that most of the time was spent in the two-way send receive operations,
which at this point were implemented using first a pulse forward and then a
pulse backwards. We expect that when using more than one node, the maximum
collective would be again the bottleneck due to its increased cost.
|
Group
|
1 node, 32 cores
|
16 node, 512 cores
|
|
|
MPI (s)
|
SHMEM (s)
|
MPI (s)
|
SHMEM (s)
|
|
Total
|
2231.71
|
2189
|
480.01
|
530.52
|
|
USER:
|
1775.49 (79.6%)
|
1979 (90.4%)
|
144.00 (30.0%)
|
195.54 (37%)
|
|
|
|
|
|
|
|
MPI
|
411.31 (18.4%)
|
31.90 (1.5%)
|
257.38 (53.6%)
|
54.46 (10.3%)
|
|
MPI_SendRecv
|
310.99 (13.9%)
|
31.76 (35.5%)
|
109.46 (22.8%)
|
49.83 (9.4%)
|
|
MPI_AlltoAll
|
43.90 (2.0%)
|
|
126.25 (26.3%)
|
|
|
MPI_Sync
|
44.90 (2.0%)
|
1.83 (0.1%)
|
78.62 (16.4%)
|
1.68 ( 0.3%)
|
|
SHMEM
|
|
61.53 (2.8%)
|
|
65.69 (12.4%)
|
|
shmem_wait
|
|
27.87 (1.3%)
|
|
11.16 (2.1%)
|
|
shmem_int_g
|
|
11.82 (0.5%)
|
|
22.71 (4.3%)
|
|
Total comm.
|
411.31 (18.4%)
|
93.43 (4.2%)
|
336 (70%)
|
121.83 (23%)
|
The table above shows the time spent in the different groups
of profiling analysis according to Craypat when using 1 and 16 nodes with
100000 iterations of the ADH test case. The last row of the table, Total comm, shows
the sum of the time spent in MPI and the time spent in SHMEM. Notice the drastic reduction in the time
spent in communication when using SHMEM. However, it is worth noting that the
USER time has increased. This is because of the active waiting of the shmem_wait_for_previous_iteration. This
time comes from the imbalance of the application and the problem being
executed. The imbalance time in the MPI implementation is shown as time spent
in SendRecv or Recv, but this comes
to user code in our implementation. Notice however that the shmem_wait
routines, which also are affected by imbalance, are included on the SHMEM time.
It is worth noting also that the maximum collective does not
show up in the profiling report. The heuristics added to reduce the number of
overall synchronisation improve the performance of the SHMEM implementation.
Disabling these heuristics increases the walltime of the SHMEM implementation
up to a 20%.
This experimental data make us believe that the fine-tuning
of these heuristics may improve the performance. In particular, tuning these
heuristics for the particular conditions of each execution (maybe by the means
of a user variable or configuration) could enhance the performance of the
different executions.
The following subsections illustrate the performance
obtained with the benchmark codes. This performance figures are extracted from
the timing table provided by GROMACS. Performance (ns/day) is the overall
performance of the execution, DD is the time spent in Domain Decomposition and
PME is the time spent computing the PME.
Since we are using these internal counters, the imbalance of
the application will affect time measurement, thus, even the lower time spent
in communication will be hidden by its effects.
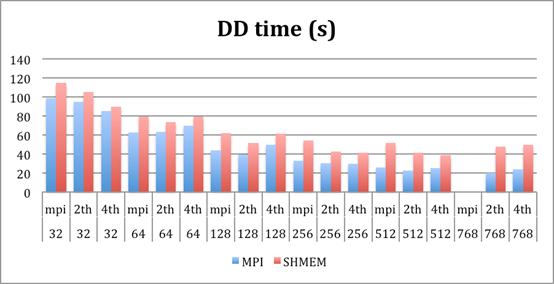
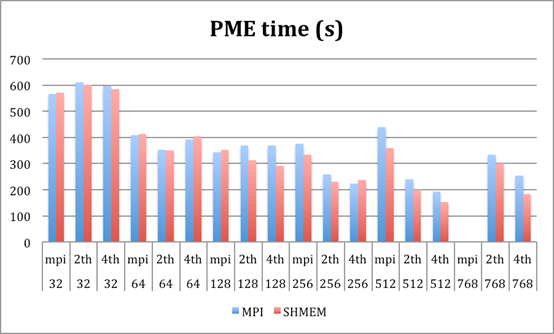
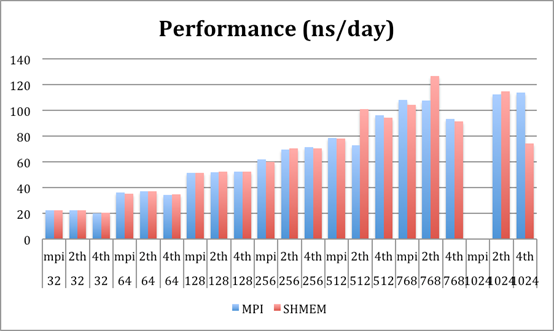
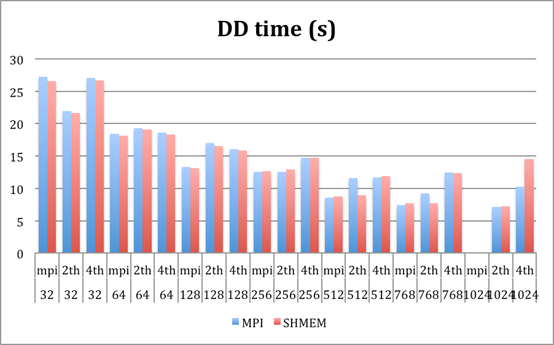
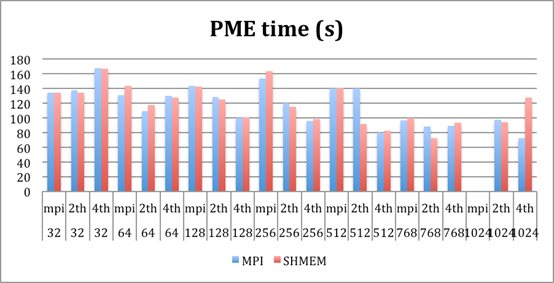
45k molecules
In this project we have explored the different possibilities
of implementing a one-sided programming model in a large code base, such as GROMACS.
Although initially the idea sounded promising, various implementation details
affected the final performance results.
We have presented a paper, titled Introducing SHMEM into
the GROMACS molecular dynamics application: experience and results, in the
PGAS 2013 conference (held in Edinburgh) where we present the results and the
recommendations for other PGAS developers.
Many decisions in the existing code, aimed to improve the
performance of the MPI implementation, limited the applicability of SHMEM.
For example, some routines compressed data into a buffer in
order to produce a single MPI Send Receive call.
This is not required in SHMEM, where it would be possible to
directly send the data to other ranks in separated put calls with lower
overhead.
Ideally, in SHMEM programs the memory is allocated at the
very beginning of the program, thus the implicit barriers are not a problem.
However this is not possible in GROMACS, where the data that is communicated is
reallocated during the execution.
In addition, the SPMD model of SHMEM contrasts with the MPMD
approach of GROMACS. Although it would be possible to replicate the allocations
of the PME nodes into non-PME nodes and vice versa, the development cost would
excess the time allocated for the project.
An alternative implementation using MPI one-sided
communications, recently adopted in the MPI 3.0 standard, may be seen as better
suited given the circumstances. The development effort and analysis performed
during this project will leverage the implementation costs a future MPI
one-sided approach, as the major areas of improvement and the refactoring has
been already performed.
This work
was supported by Dr Berk Hess at KTH.
This
project was funded under the HECToR Distributed Computational Science and
Engineering (CSE) Service operated by NAG Ltd. HECToR A Research Councils UK
High End Computing Service - is the UK's national supercomputing service,
managed by EPSRC on behalf of the participating Research Councils. Its mission
is to support capability science and engineering in UK academia. The HECToR
supercomputers are managed by UoE HPCx Ltd and the CSE Support Service is
provided by NAG Ltd.
References
[1]
GROMACS website , http://www.gromacs.org/
[2]
HECToR website, http://www.hector.ac.uk/
[3]
OpenSHMEM website, http://openshmem.org/
[4]
Cray Profiling and Analysis Tools documentation in HECToR, http://www.hector.ac.uk/support/documentation/userguide/tools.php#craypat
Discussions with
the development team have raised some ideas to overcome the limitation of using
the same number of PME and PP nodes in the SHMEM implementation. Some of these
ideas are described below as future reference
Building separate PP and PME binaries and using the aprun
MPMD capabilities to launch two separate executables on the same MPI_COMM_WORLD
communicator may overcome the limitations of the memory allocation. Changes in GROMACS
would be simple.
However, current Cray SHMEM implementation does not support
multiple binaries, thus, this is not viable on HECToR.
Discussions on the OpenSHMEM mailing lists are being held on
adding support for subgroups of processors in SHMEM. Whether this will include
in future releases or not is yet to be officially communicated.
If the SHMEM standard adopts this functionality, the GROMACS
SHMEM implementation could be easily modified to support this feature.
Since the PME part of the code only requires an intermediate
communication buffer allocated in symmetric memory, and it is currently
allocated at the beginning of the program, it would be possible to use the PME
part only on a subset of the nodes. However, it is not possible to not execute
the PP part, as it contains many memory reallocations that cannot be easily
replicated on the PME-only nodes.
The current implementation decides before starting the
molecular dynamics simulation if a particular node is a PP or PME only. If the
number of PME-only nodes is set to zero, the current implementation forces that
all nodes are PP and PME.
A detailed analysis of the code reveals that it would be
possible to modify the code enabling a new alternative where PP nodes can be
PP-only or PP and PME.
Rather than using a Split Communicator operation when
splitting the ranks in the domain decomposition, the PP communicator would
continue to be the whole rank, and the PME rank would be the subset. The
communication between PME and PP nodes would need to be adjusted to ensure the
proper redistribution of data. Currently, The PP nodes check whether if they
are PME also and, if not, they communicate the forces to the PME nodes. This
check, both in sender (dd_partition_system)
and receiver (dd_forces_lowlevel), would need to be modified to acknowledge the possibility
of PP+PME nodes or PP-only nodes.
However, the most complex part of this modification is
adding the code required to perform the PME in a subset of nodes without using
the PP part of the code.
Since the current PME-only or PP-PME decision is held before
the PP part, it would be necessary completely refactor the PP part to (1)
disable the current PME implementation which does not communicate the forces
but assumes local memory and (2) create a call to the PME-only part of the code
after the force computation and before the receive of the forces from the
PME-only nodes.
These changes require a noticeable effort and a deep
collaboration with the GROMACS team, as it affects the development of future
versions of the software. Since the GROMACS package is currently suffering a
major re-factoring, this feature would need to be discussed in the future.












