Graph
1: Efficiency for 256,000 atoms of Argon
Table of Contents
2 Work Package 1: Implementing an Extended VNL scheme 2
DL_POLY_4i is a general purpose classical Molecular Dynamics (MD) simulation software package which has been developed at STFC Daresbury Laboratoryii by I.T. Todorov. The package is used to model the atomistic evolution of the full spectrum of models commonly employed in the materials science, solid state chemistry, biological simulation and soft condensed-matter communities. It has been developed under the auspices of CCP5iii and is widely used throughout the UK as well as world-wide. It is a fully data distributed code, employing methodologies such as spatial domain decomposition, link-cells, Verlet neighbour listiv and the 3D Daresbury Fourier Transform (DaFT)v. The code demonstrates excellent performance and has been shown to scale to large numbers of processors.
This proposal comprised two work packages which will improve the effectiveness of DL_POLY_4. The first work package concerns the redesign of the Verlet neighbour list (VNL) calculation within the linked cells (LC) scheme. It targets the implementation and modified utilisation of an extended VNL which will be conditionally updated at every few timesteps rather than at every timestep. This is described in section 2. The second improvement, multiple time stepping, regards the implementation of a symplectic scheme using the Reversible Reference System Propagator Algorithm (RESPA) for less frequent calculations of expensive operations such as long-ranged Ewald and short-ranged inter-molecular evaluations. The speed up of this feature will be conditional upon user specifications.
In all results presented below the runs have been either on HECToR itself or the the HECToR test and development system (TDS). Also for all results version 4.6 or later of the GNU compiler suite has been used. However it should be stressed that the code has been tested on a number of other clusters and workstations, and with other compilers especially through the development stage.
The linked cells (LC) algorithmvi is an excellent method to parallelise a molecular dynamics calculation by using equispatial domain decomposition (DD). The simulation cell is divided into a number of equal volume domains, and each domain is assigned to an MPI process. As atoms only interact with each other over a finite distance, the “cutoff”, only position data for atoms near the edges of each domain need communicating for the atomic interactions to be calculated, provided the cutoff is much smaller than the length of the edge of the domains. The LC method thus has much in common with the halo exchange methods used in solving differential equations on grids, except that it is generalised to allow for the “grid points”, i.e. the atoms, to be disordered in space, and for them to move from time step to time step. Every timestep the LC algorithm is used to construct a domain specific list of all unique pairs of atoms. This list is then used in all pair force evaluations such as Van der Waals, metal, short-ranged Ewald and its estimates as well as for RDF calculations.
The list evaluation is costly and can takes as much as 40% or 90% of the compute time per timestep for systems with or correspondingly without Ewald summation requirement for their electrostatics evaluation. This can be algorithmically reduced without much expense on memory by enlarging the DD cutoff by a small distance (referred here as shell or padding) and keeping track on how far particles travel form there position at an update point. At each timestep after the VNL update it is tested if any particle has travelled more than half the shell distance in any direction. Only when is this the case the list is updated. Despite the simplicity of the procedure there will be a number of important implications for the rest of the code. The most serious of which is that the DD neighbours' communications of domain crossing particles and associated intra-molecular entities must be held off during steps when no VNL update is necessary whilst all other communications function as usual. Furthermore, despite no halo exchange and no local reordering are needed, a full positional halo refresh must occur. Finally the implementation of periodic boundary conditions needs careful consideration throughout the whole programme.
The basic idea behind the method is, in essence, to decouple the length of the side of a link cell as used by the simulation with the length of the potential cut off. Instead the new link cell side will be at least the cut off plus the shell width specified the user. The nett result therefore of the method will be a code that uses slightly larger link cells. This has implications not only for the implementation but also for the performance of the method.
The implementation requires the following steps
Implement reading the shell width from the CONTROL file
DL_POLY_4 used the variable rcut throughout to indicate both the side of a link cell and the potential cut off. The first step in decoupling the link cell size and the potential cut off is therefore to introduce rlnk which will be the new side of a link cell. This required special care in the routines where the cut off and the link cell size are being made commensurate with the size of the simulation cell
Work through the 30+ routines that used rcut determining whether it should be replaced by rlnk. This again required care as some routines use rcut in both senses, and also did require changes to argument lists in a number of places to pass rlnk as appropriate.
Implement generating the VNL for the new larger link cell size
Regression testing that the code still works, i.e. check that the decoupling is correct and works for the case where the modified VNL update is invoked every time step
Implement data structures to track the motions of the particles. This was made general as it has other potential uses in the code, mean square displacements of atoms being an obvious one. Note that as DL_POLY_4 is a totally data distributed code this requires a small amount of extra communication when an atom moves from one domain to another, as the tracking data associated with it needs to be communicated to the process holding the new domain as well as the atom itself.
Implement detecting when any particle in the simulation has moved sufficiently far to trigger the need for a VNL update
If a VNL update is not required:
(Optional: Compress the VNL)
Avoid calling the routines that export atoms to the appropriate neighbouring domain
Modify the routines that update the halo of a domain appropriately
Check that periodic boundary conditions are still being correctly implemented
Regression testing of the new code for a variety of shell widths
Steps 8 and 9 require some expansion, while point 10 ultimately also provided the numbers reported in the results section.
For step 8 we will address the second and third sub-points before returning to the first. Avoiding a VNL update means that the particle should remain on the process that originally calculated what neighbours that particle has, as that is the only process with this information, DL_POLY_4 being a fully distributed memory code. (It is best to avoid communicating the neighbour list as it is a large object and so would incur significant overhead). Now as the particle has travelled this can result in a sort of “blurring” of the domains as the particle may now be outside the spatial domain strictly owned by its process. In the old code this would mean the particle is communicated to the process holding the appropriate neighbouring domain. However now we must avoid this communication because that process will not possess the appropriate neighbour list. Thus VNL shelling will also involve a small but important reduction in the amount of communication required. It is small because only a relatively small number of particles cross a domain boundary at each time step, important because this means the messages are short, and therefore latency bound.
However, while the export stage may be avoided the resetting of the halos can not. The halos consist of particles which are owned by neighbouring process, and after a positional update these particles need re-communicating as the values in the reference process will no longer be up to date. This caused a problem in that a process in DL_POLY_4 may completely re-order its particles at each timestep. This is for a number of efficiency reasons which are not really relevant here. Thus process A could re-order its particles and then send the appropriate ones to process B to update the halo of the later. Now if the VNL is being updated each step this is not a problem. However, if this is not the case the situation can arise where the VNL has been calculated according to the original ordering of the particles owned by process A, but this is no longer appropriate. Thus to avoid this new routines had to be added which “deported” the halos with the appropriate ordering (i.e. that when the last VNL update occurred) to ensure that the interpretation of which particle is which within the halo is correct on the remote process. It is worth mentioning that this halo refresh update of positions is crucial for the correct charge density when transitioning from particles charges to a charge grid as otherwise blurring will lead to wrong density and thus wrong electrostatics evaluation.
We now return to the first point in step 8 above, VNL compression. This was an attempt at optimising the use of the VNL. Let us assume that the simulation of interest uses a fairly complex force field. In such a case the VNL may be employed in evaluating quite a range of terms, an incomplete list being Van der Waals, short range Ewald and other electrostatic terms, radial distribution functions, and various metal potentials. In each of these the loops will be over the whole neighbour list. However, due to the shell a number of the pairs will correspond to atoms that are separated by more than the cut off, and so the interaction will be zero. Thus in certain cases it may be beneficial to produce a “compressed” VNL which is appropriate for just this time step from the full VNL which omits all pairs which are further apart from the cut off. This compressed list can then be used in the evaluation of the terms noted above, which one would hope would be somewhat more efficient. In practice we found the benefit to be small. This is probably due to a number of reasons, the main being
Each term can have its own cut off. The compression must work off the largest, and thus for some terms there may well be many remaining interactions which are still zero. It also means that we can't avoid the conditional on the distance in the inner loop of the force evaluation
For compression to work well the VNL must be used by many terms, as it will avoid the evaluation of many zeros in the inner loops. In practical calculations the force fields are such that it is rare that more than 3 will be used, and indeed some of the interactions in the above list are incompatible on basic physical terms (for instance any form of electrostatics and metals). 3 is probably not enough to make compression a large optimisation.
Thus while the final code does include list compression it will not be covered further as the nett effect in practical calculations was found to be small.
Step 9 results from the “blurring” of the domains mentioned above, as now a particle may be positioned such that it is not strictly in the spatial domain of the owning process. Originally DL_POLY_4 assumed a strict mapping of the particles to the area of space mapped to the process. The breakdown of this assumption caused a number of subtle effects in the code, the most important being how periodic boundary conditions are handled, and the related issue of calculating pair separations. For instance problems could arise if a particle moved outside the right edge of the simulation cell, but due to the extended VNL scheme was still owned by a process on the right edge of the box. The original code would assume it was now held by a process on the left edge of the box and shift the position by the appropriate lattice vector. This could now cause the interatomic separations to be incorrectly calculated as the process actually updating the atom effectively “sees” the atom at the position before the shift, not after. This all required careful consideration (and a period of frantic picture drawing and confused telephone calls between Drs Bush and Todorov!). Again, this halo refresh update of positions is crucial for the correct charge density when transitioning from particles charges to a charge grid as otherwise blurring will lead to wrong density and thus wrong electrostatics evaluation.
Thus the implementation was reasonably straightforward apart from a couple of fiddly places. The nett performance effect of all these changes is quite complex. In the next section we will present some performance results, but just to summarise the effects that may be expected
If the shell is sufficiently wide and the particles are moving sufficiently slowly the VNL will be only occasionally updated. Thus this should result in a performance gain.
Occasional VNL updating means atoms need to transferred between domain more rarely and possibly in larger quantities due to the domain blurring. This will result in less frequent communication with possibly slightly larger message sizes, leading to less and more effective communications and thus small performance gains.
The use of a shell will make the VNL itself a little larger. As evaluation of the forces requires looping over all the VNL this may lead to a small performance loss.
The use of the shell makes the link cells bigger. Thus
Where all particles in the extended domain (including the halo) need be looped over this will be more expensive. This affects evaluation of the VNL itself and also 3 and 4 body terms.
The larger link cells mean a thicker halo, and hence more communication when resetting the halos.
Thus provided effects 1 and 2 are dominant, which we expect to be the case, we should see a performance gain.
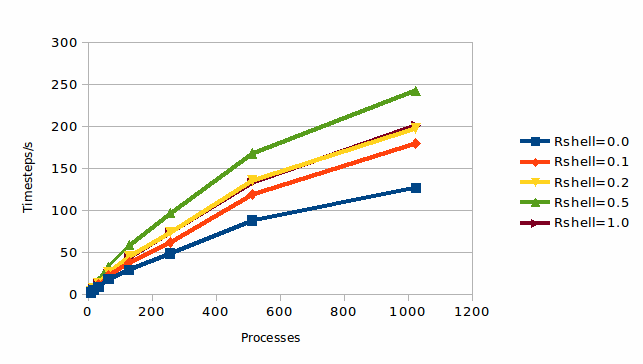
We first consider a very simple simulation, that of 256,000 atoms of Argon at 4.2K. The force field consists solely of Van der Waals terms (as a Lennard-Jones potential), and thus construction of the neighbour list is a comparatively expensive operation for this simulation. This is both (i) because the force field is so simple and therefore quick to calculate, and (ii) because there is only one term in the force field and therefore there is no reuse of the neighbour list in multiple terms. Thus avoiding calculation of the neighbour list should be very beneficial, and this is further helped by the temperature being very low meaning the atoms are barely moving at all. This last point should mean that the neighbour list only needs recalculation very infrequently. All in all this should be close to a “best case scenario” for the method!

Graph
1: Efficiency for 256,000 atoms of Argon
It can be seen that the expectations are largely borne out. A shell of 0.5 Å results in a approximate doubling of the performance of the code, which is as expected as the construction of the VNL is significantly more expensive than the actual evaluation of the forces. This also suggests that the VNL is only being very rarely recalculated, which is indeed the case. For a 0.5 Å shell the calculation of the VNL is being skipped over 90% of the time.
It can also be seen that the larger 1.0 Å degrades the performance. This is due to a number of reasons (as discussed above), the most important being that
The larger shell implies a larger VNL which contains extra interactions which correspond to pairs of atoms further apart that the cut off of the potential. Thus some loops needed at each timestep, either in the evaluation of the potential or in the compression stage, will be over this longer list even if most terms are rejected, and therefore will increase in expense as the shell is made larger.
Larger link cells, as implied by the larger cell, also imply thicker halos and so mean more atoms must be communicated when the halo update or refresh occurs at the end of each timestep. Thus again a larger cell can result in more computational expense.
Thus this simple example both behaves as we expect, which is satisfying, and illustrates the point that for each simulation case there will be an optimum width of the shell. To get the best out of the method will, therefore, require some experimentation by the user. This will typically consist of a few short runs with a limited number of timesteps, and measuring the performance as a function of the width of the shell. However, we will make some general recommendations for suitable “first guesses” later in this report.
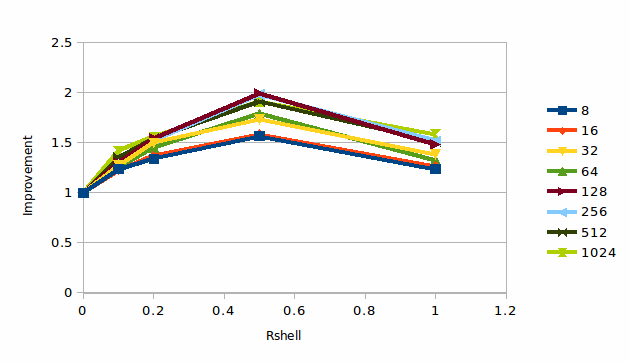
Graph 2 illustrates this point by showing how much faster the simulation runs as a function of both the shell thickness and the number of MPI processes. It can be seen that there is a clear maximum in the performance for a shell of 0.5 Å
Graph
2: The improvement due to shelling for 256,000 atoms of Argon
Despite its simplicity the Argon case is representative of the behaviour seen for other cases – a small shell can result in an appreciable improvement (though rarely as large as above) and up to a certain point scalability can improve, but a thicker shell degrades performance. It is not always as easy to diagnose each case, for after all the best thickness of the shell depends upon the detailed dynamics of the material and it is to solve that problem that we are performing the simulation in the first case, but we shall illustrate the behaviour with two more cases.
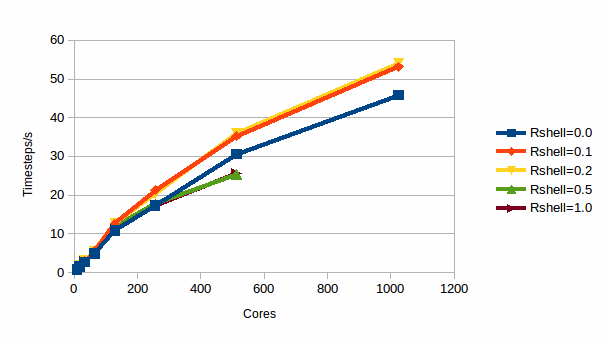
The first is 216,000 ions of common salt simulated at 500 K. Compared to the previous case this simulation requires more complex force field which now contains the expensive electrostatic terms and so means the the VNL update is relatively less expensive. Further the higher temperature implies greater atomic motion, and hence one would expect that the VNL update can be skipped less often. We therefore expect a less dramatic improvement, and the results are shown in graph 3
Graph
3: Efficiency for 216,000 atoms of NaCl
It can be seen that for this case a thin shell of 0.1-0.2 Å results in a much more modest improvement of approximately 20%. It can also be seen that the lines for the thicker shells finish at 512 cores. This is because the shell implies a larger link cell, and thus the minimum size of a computational domain is also larger. Therefore, the maximum number of domains that can fit in the computational box is reduced, and hence so is the maximum number of MPI processes that can be used. In this case the increased link cell size has resulted in it not being possible to run the simulation on 1024 cores.
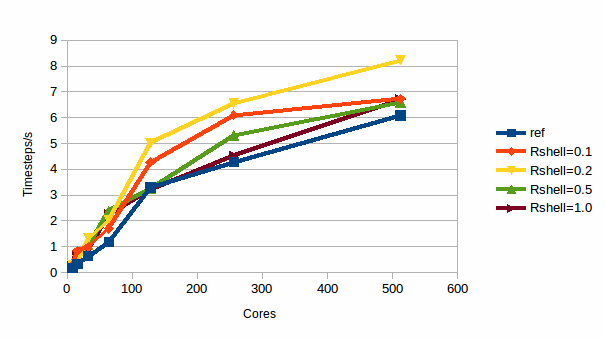
The next case we shall consider is a the TIP4P model of water. The simulation contains 232,416 sites and has been run at 295K, and the water molecules are modelled with rigid bodies. Graph 4 shows the results.
Graph
4: Efficiency for TIP4P water
For this more complex simulation the best shell thickness is less clear and depends upon the number of cores, but a pragmatic conclusion is that a 0.2 Å shell is a good choice across much of the range and can give a roughly 30% or better improvement in performance. However, it is now difficult to diagnose exactly what contributions are causing the shape of the observed curve.
The modified VNL update code has been checked against all 46 of the standard DL_POLY test cases for a shell thickness of 0.1, 0.2, 0.5 and 1.0 Å and also on a wide range of core counts. In the vast majority of cases a marked improvement in performance was observed, and across all cases an average improvement in run time of ~ 20% was achieved. It is probable that this figure could be improved with a more thorough search, but in the time scales available this was not possible. Throughout these tests it was also observed that a shell thickness of 0.2 Å, while not always ideal, was generally a good “first guess” at the thickness.
The only cases where a marked degradation was observed was for simulations involving 3 or 4 body forces, and this can be traced back to the larger link cells implied by the method. To see why this is it is best first to remember how the VNL for the two body terms is actually constructed: The box is divided into link cells, and then the VNL is constructed using the fact that the only atoms a given atom can interact with are in its link cell or neighbouring ones. Thus it can be seen that larger link cells will result in the VNL being more expensive to construct as more atoms must be considered, but this effect is alleviated by the shelling allowing us to only construct the VNL occasionally. The VNL is then used within the force evaluation inner loops to select which atoms interact. One could follow a similar procedure for the three body terms, but the resulting three body neighbour list would consume unacceptable amounts of memory. Thus instead DL_POLY uses the link cell structure to determine neighbours while inside the main 3 body loops, effectively generating the 3 body neighbour list on the fly. This save huge amounts of memory but does mean that it suffers from the effects of increasing extended domains (including their now thicker halos), and also it need be done every time step. Hence VNL shelling can have a marked negative effect on the time to solution for problems that use three body terms, and four body forces are similar for the same reasons.
The code has been merged with the main branch and should be released to users soon.
The extended VNL scheme described in the proposal has been completed. For the vast majority of simulations a marked improvement of the order of 20% can be observed, and a shell of 0.2 Å is often a good first guess, though one must experiment a little to find the ideal choice. The one exception to this is for simulations involving 3 and 4 body forces, where a marked decrease in performance may be observed. Due ultimately to memory constraints they can not exploit the new scheme advantageously, and thus should avoid its use.
Multiple time stepping is a feature especially popular in, although not limited to, the biochemical area of computational chemistry. The idea of symplectic multiple time stepping, RESPA, was first suggested by Tuckerman, Berne and Martynavii and elegantly researched by Humphrey, Freisner and Berneviii. The idea behind the methodology is to exploit the fact that different terms in the force field evolve on different time scales. For instance the long range contribution to the Ewald terms changes only very slowly when compared to terms involving intra-molecular motion, such as vibrations. Now, as is usual with the numerical integration of differential equations, the fastest motion determines what the timestep must be to ensure numerical stability of the solution (c.f. The Courant-Fredrichs-Lewyix condition). However, in standard molecular dynamics every term in the force field is evaluated at every timestep. Thus if a very short timestep is required to correctly integrate molecular vibrations, it will also force the evaluation of the long range Ewald potential at every timestep, despite the later hardly varying at all on the time scale being examined. This can be very expensive, and instead the RESPA method provides a way to evaluate the slowly varying terms in the user specified force field only when required, whilst both keeping the short timestep required for the more quickly varying terms, and only causing a small degradation in the quality of the results. Thus as certain terms are only evaluated infrequently rather than at every step one would hope for an improvement in time to solution.
The mathematics of RESPA ultimately depend on the Trotter expansion of the Liouville propagator. In terms of the software the nett result is fairly straightforward. The terms in the MD force field are split into a number of classes and the fastest varying terms (class 1) are evaluated every timestep. Every n1 timesteps the next most quickly varying (class 2) are updated. Similarly every n2 times class 2 is evaluated (and hence at n1*n2 evaluations of class 1) class 3 is updated, and so on to the very slowest varying class. When combined with a velocity Verlet type integrator within an NVE ensemble the (ancient) Fortran-like pseudocode for 4 classes is (taken from Humphreys et al.)

Figure
1: "Pseudocode" for a 4 class RESPA implementation
It can be seen the class 4 forces are evaluated only once per large cycle, so if these are comparatively expensive this scheme can markedly reduce the time for the whole simulation. It can also be seen that the parameters required for RESPA that differentiate it from a conventional MD run are simply n1, n2 etc. in the above. In our implementation we follow the four class method, so in what follows a run may be characterised by these three numbers. Thus we will denote a run with n1=1, n2=4 and n3=2 as “1:4:2”. We shall also use 1:1:1 as shorthand for a conventional, non-multiple time stepping, molecular dynamics run.
The multiple time stepping, and in particular these 3 numbers, are controlled by the user. Larger values will lead to larger computational speed-ups as more evaluations of certain terms in the force field are avoided. However it will also lead to worse energy conservation, and it is up to the user to find suitable values for the specific cases they are interested in.
As noted above we follow the 4 class implementation of Humphrey et al. Thus the first job is to classify the terms in the DL_POLY force field. We adopted the following break down of the force terms:
Class 1 (i.e. fastest varying): Core-shell, tethered atoms, harmonic bonds
Class 2: Tersoff, three body, four body, angles, dihedral, inversions
Class 3: Metal, Van der Waals, “Short range” electrostatic terms (including Ewald)
Class 4: (i.e. slowest) “Long range” Ewald
It can be seen that physically classes 1 and 2 are intra-molecular terms, 1 corresponding to (extremely!) approximate electronic effects and hard vibrational modes, class 2 to essentially soft vibrational modes, while 3 and 4 deal with inter-molecular effects. Please also note that each of the above short descriptions may cover more than one routine within the code, as each type of term my be modelled in more than one way.
Thus in essence the implementation is fairly straightforward
Implement storage of the 3 integer parameters as required by the method
Implement methods for the user to set these parameters
Add code to analyse the force field being used by the simulation to identify which classes are being used
Using that classification make sure that the routines implementing those terms are only called if the appropriate class is active. Note that both this stage and the previous are large jobs in themselves due to the complexity and generality of the force field supported by DL_POLY_4
Adapt the integration schemes to the scheme roughly outlined in the introduction
While in principle this is straightforward as always with programming the devil is in the detail. One such devil is that in a number of cases the factorisation into classes is not complete. The most problematic of case of this for us was for the constant pressure integration algorithms, something we shall return to later, but a simple example is the removal of the motion of the centre of mass of the system. This is essential in molecular systems to avoid the infamous “flying ice cube”, but is also a very good idea for periodic systems. This does, however, require the total nett force on the system which, within the RESPA framework, method may not always be possible to calculate because the appropriate force terms may not be up to date.
However, the main daemon we encountered were the integrators. To cover all common simulation cases integrators are required for the following cases
NVE – i.e. a simulation with a constant number of particles (N), with a constant cell volume (V) and a constant total energy
NVT – i.e. constant number, constant volume, constant temperature
NPT – i.e. constant number, constant pressure, constant temperature
Note both isotropic and anisotropic pressure tensors are required
Rigid bodies – typically each integrator comes in two forms, one dealing with rigid bodies, one that deals with the simpler case where they are not present
Note that both NVT and NPT can be implemented by a number of ways, and each variant has different strengths and weaknesses, and DL_POLY_4 supports a variety of these methods in each case. We also note that the discussion so far has assumed a velocity Verlet (VV) type integration method, while DL_POLY_4 supports note only VV but also leap-frog Verlet (LFV). The nett result is that DL_POLY_4 supports 60 integrators, each of which in principle needs to be changed to implement RESPA!
To simplify matters it was decided a priori not to support the LFV methods within RESPA. This is ultimately because the mathematics for RESPA under the LFV method are only approximate as it does not work with the Trotter expansion, while the VV method does not have this difficulty. Still 30 integration schemes to implement and test fully is a large amount of work, and it was in this point that we realised the original proposal was a little too ambitious. This rapidly became clear once we reached this stage of the implementation because it was not appreciated quite how much change would be required in each of the integrators when the proposal was written. In practice while a simple NVE, non-constrained integrator is straightforward (and that is what the scheme outlined in the introduction addresses) in a real, general purpose molecular dynamics code the addition of such features as constraints, thermostats, barostats and similar markedly complicates the code. In fact the changes themselves are not that complex, at least for the NVE and NVT ensembles, and mainly require the integrator to know which class it is dealing with to allow it to make the correct updates of positions and velocities. This can be seen in the scheme above where while at all class levels the velocities are updated it is only for the most quickly varying class that the positions are updated, and this especially complicates the implementation of constraints. These require an iterative update scheme that should only be applied for the innermost class. Another change that is class dependent is the scaling of the time scale in the velocity updates. A further small complication is that the most quickly varying class is not necessarily class 1 as it depends on what terms are in the force field used by the simulation. The current implementation carefully avoids overheads due to calling routines that result in “no operation” due to the force field not containing terms in the appropriate class.
So we found that a larger number of small but detailed changes were required than we originally anticipated, and that that was in a large number of fairly complex routines. It was found to be particular hard for NPT ensembles and rigid bodies, and as a result integrators using either of these classes were not completed (though work has been started in both cases). As this has now been addressed in a subsequent proposal we will only briefly explain the issues encountered here, but the essence is as follows.
For a constant pressure simulation the size of the simulation box must change as required to preserve the pressure. This may be a simple scaling of the lattice parameters in the isotropic case, or it may be that the whole box shape can change in the anisotropic case. These changes depend on the total virial for the system, and this immediately highlights the problem, as within the RESPA scheme the total virial may not always be available, or at least up to date. Coupled with this are the fact that changing the box shape will change the coordinates of the particles in space, further complicating the integrator. In fact special variants of the RESPA scheme have been developed to deal specifically with the constant pressure scheme (e.g. XI-RESPA and XO-RESPAx), and it is these that the follow up proposal will need to implement.
Rigid bodies complicate the scheme because they don't only have a velocity and position that needs updating, they also possess angular momentum, something point particles obviously lack. Outside of a RESPA scheme it is straightforward if a little complicated to implement the integrator without reference to angular momentum or similar quantities and this is how it is done in DL_POLY, where the required operations are expressed in terms of quaternions. Whilst this is very efficient, in the mathematical expressions that result it is not entirely obvious that the application of the forces from the for individual classes in turn will be the same as applying the total force all at once (obviously this must be true within the approximation of the RESPA shadow Hamiltonian). This opacity further complicates the implementation of RESPA within an already complex set of routines, and as a result the work in this are has also not been completed.
Thus in summary we have successfully implemented and fully tested the NVE integrator, and also all 6 NVT integration schemes which do not use rigid bodies. Partially completed schemes exist for some NPT and rigid body routines. In each of these cases they have been shown to run correctly for n1=n2=n3=1 (a very important first step), but time was not available for full testing and debugging and thus we feel we can not claim these integrators are ready for release. However it must be stressed that those that have been completed do allow a wide range of important and interesting work to be accomplished, and it will be shown in the next section that they can result in a very appreciable improvement in performance.
|
RESPA Parameter |
Average Energy |
%Energy Difference |
RMS fluctuations in energy |
RMS/Energy |
Time/s |
% Time difference |
Timesteps/s |
|
1:1:1 |
-9.6965*108 |
0.000 |
47.5600 |
0.0000000 |
42.5 |
0.00 |
12.06 |
|
1:1:2 |
-9.6965*108 |
0.000 |
50.8530 |
-0.0000001 |
34.0 |
-20.03 |
15.08 |
|
1:1:4 |
-9.6965*108 |
0.000 |
78.1280 |
-0.0000001 |
27.0 |
-36.40 |
18.96 |
|
1:1:8 |
-9.6965*108 |
0.000 |
266.9400 |
-0.0000003 |
27.0 |
-36.40 |
18.96 |
|
1:1:16 |
-9.6965*108 |
0.000 |
1072.0000 |
-0.0000011 |
26.3 |
-38.18 |
19.50 |
|
1:1:32 |
-9.6967*108 |
-0.00825 |
12504.0000 |
-0.0000129 |
26.0 |
-38.80 |
19.70 |
|
1:1:64 |
BREAKDOWN |
|
|
|
|
|
|
Table 1: 27,000 atoms of NaCl on 128 Cores
The table above shows the results for a simulation of 27,000 particles of common salt using an NVE ensemble on 128 cores, by DL_POLY_4 standards a small simulation. 2048 timesteps were used, and the simulation was carefully equilibrated before the measurements reported above were taken. This simulation only has class 3 (Van der Waals, Short range Ewald) and class 4 (Long range Ewald) terms, and so is a simple example of the use of RESPA. The conservation of energy, the time to solution and the quality of the integration is shown as a function of n3, the only RESPA parameter that can be (meaningfully) varied. This has been systematically doubled until a value of 64 has been reached, by which time the integration scheme breaks down totally.
It can be seen that the same average energy is reported for values of n3 up to 16, after which it is clear the calculation becomes increasingly inaccurate. This is also reflected in the steadily increasing RMS fluctuations in the energy; given this is an NVE ensemble the energy should be constant, and these fluctuations reflect increasing inaccuracies in the integration of the equations of motion. It can also be seen that the time to solution decreases systematically with an increase in n3. Thus the system is behaving as expected – for a small decrease in accuracy a substantial decrease in time to solution can be achieved, and the more the requirement of accuracy is relaxed the faster the simulation runs. It can also be seen that a choice of 1:1:4 for the RESPA parameters results in a very modest decrease in the accuracy of the simulation but also a marked decrease in simulation time.
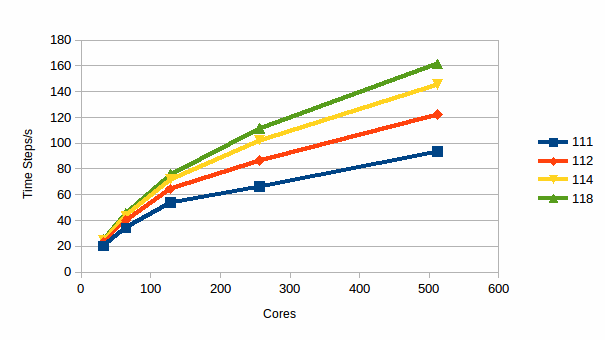
Graph
5: Timesteps/s for 27,000 atoms of NaCl
Graph 5 shows the computational efficiency of the calculation as a function of both the number of cores and the RESPA parameter in terms of the number of timesteps per second that can be achieved. It is clear that use of RESPA can provide a very marked improvement in the number of timesteps/s, and so also in time to solution, for all core counts considered here.
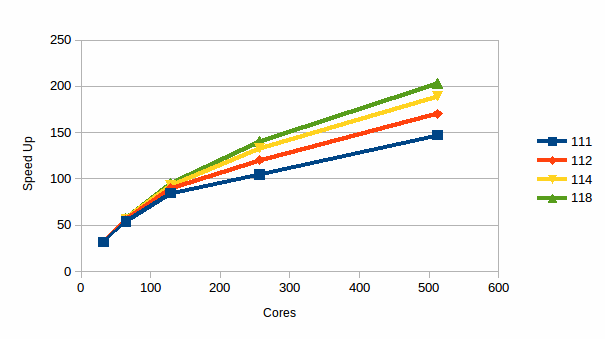
Graph
6: The Speed Up for 27,000 atoms of NaCl
Finally for Sodium Chloride graph 6 shows the speed up as a function of the number of cores and the RESPA parameter. The figure assumes perfect speed up to 32 cores, and is relative to the value measured for the particular RESPA parameter, i.e. the 1:1:2 curve is speed up relative to a 1:1:2 run on 32 cores, while the 1:1:4 curve is relative to a 1:1:4 run again on 32 cores. We show this graph to show that RESPA is capable of not only increasing computational efficiency of the calculation, it can also increase the scalability (graph 5 conflates these two issues, while graph 6 focuses purely on the parallel scaling). It can be clearly seen that this is the case, and indeed it is a rare example of “having your cake and eating it”! Here the reason is that an increases in n3 reduces the number of times the class 4 terms, i.e. the long range Ewald terms, need be calculated, and so emphasises the class 3 terms. The long range Ewald terms are expensive and also require a parallel, distributed memory FFT. This last operation scales less well than many other parts of DL_POLY_4, and in particular less well than the halo exchange based link cell algorithm that is used for the class 3 terms. Hence the improvement in scalability.
The next test case we consider is one a simulation of 69,120 atoms of a Sodium/Potassium Disilicate glass, again a fairly small simulation. Once more the system was carefully equilibrated and then run for 1024 timesteps. As above we consider the quality of the simulation first as a function of RESPA parameters, and then then its computational efficiency and scalability as a function of the number of cores. The main difference between this case and NaCl is that not only are class 3 and class 4 terms involved (in fact exactly the same terms as before), class 2 (3 body terms) are also involved.
The results pertaining to the quality of the simulation are in table 2
|
RESPA parameter |
Average Energy |
%Energy Difference |
RMS fluctuations in Energy |
RMS/E |
Time/s |
% Time difference |
Timestep/s |
|
1:1:1 |
-2.0534*1010 |
0.00000 |
1991.1 |
-0.00000010 |
142.068 |
0.00 |
7.21 |
|
1:1:2 |
-2.0534*1010 |
0.00000 |
2020.7 |
-0.00000010 |
134.431 |
-5.38 |
7.62 |
|
1:1:4 |
-2.0534*1010 |
0.00000 |
2172.2 |
-0.00000011 |
132.506 |
-6.73 |
7.73 |
|
1:1:8 |
-2.0534*1010 |
0.00000 |
4260.1 |
-0.00000021 |
131.832 |
-7.21 |
7.77 |
|
1:1:16 |
-2.0534*1010 |
0.00000 |
59690.0 |
-0.00000291 |
132.319 |
-6.86 |
7.74 |
|
1:2:1 |
-2.0534*1010 |
0.00000 |
2406.0 |
-0.00000012 |
120.981 |
-14.84 |
8.46 |
|
1:2:2 |
-2.0534*1010 |
0.00000 |
2610.4 |
-0.00000013 |
118.981 |
-16.25 |
8.61 |
|
1:2:4 |
-2.0534*1010 |
0.00000 |
4650.9 |
-0.00000023 |
118.289 |
-16.74 |
8.66 |
|
1:2:8 |
-2.0533*1010 |
-0.00487 |
61678.0 |
-0.00000300 |
118.653 |
-16.48 |
8.63 |
|
1:4:1 |
-2.0534*1010 |
0.00000 |
6178.1 |
-0.00000030 |
112.206 |
-21.02 |
9.13 |
|
1:4:2 |
-2.0534*1010 |
0.00000 |
7754.9 |
-0.00000038 |
111.611 |
-21.44 |
9.17 |
|
1:4:4 |
-2.0533*1010 |
-0.00487 |
73402.0 |
-0.00000357 |
111.765 |
-21.33 |
9.16 |
|
1:8:1 |
-2.0534*1010 |
0.00000 |
43534.0 |
-0.00000212 |
108.165 |
-23.86 |
9.47 |
|
1:8:2 |
-2.0532*1010 |
-0.00974 |
184360.0 |
-0.00000898 |
108.372 |
-23.72 |
9.45 |
Table 2: 69,120 atoms of a Sodium/Potassium Disilicate glass on 256 cores
It can be seen that the situation is similar to the NaCl case above; increasing RESPA parameters result almost always in decreasing computational cost at the expense of reduce accuracy. The exceptions are within the observed reproducibility of the times on the machine used (the TDS for HECToR). It can also be seen that in this case changing n2, the parameter for class 2 and so in this case the 3 body forces, has a greater effect than n3 on both the time to solution and the accuracy. This suggests that the Van der Waals and short range Ewald Terms are more important in this simulation than the long range Ewald as it is the former terms that are calculated less frequently when n2 is increased, while adjusting n3 only affects the later. Looking at the output of the job supports this. In both this case and NaCl the FFT grids are approximately the same size (the grid size is a complicated function of a number of parameters, but the crucial point here is that the simulation box is approximately the same volume for both systems). Thus the FFT time will be approximately the same for this case as for NaCl, but due to there being ~2.5 times as many particles and the O(N) scaling of DL_POLY other portions of the code will be proportionally more expensive, thus emphasising the class 3 terms. It can also be seen that again at the cost of a small decrease in accuracy a marked improvement in time to solution can be achieved (e.g. 1:2:2 or 1:4:2, depending on the accuracy requirements of the simulation).
Graph 7 shows the computational efficiency.
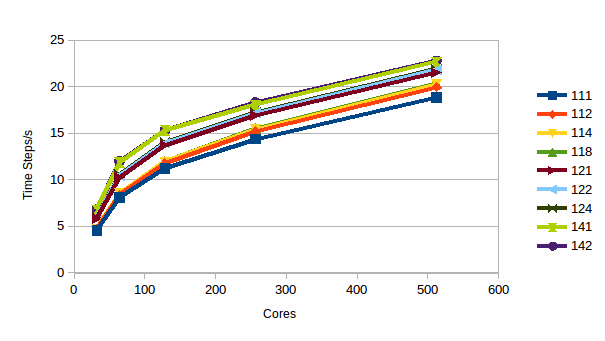
Graph
7: Timesteps/s for 69,120 atoms of a Sodium/Potassium Disilicate
glass
Again it can be seen that increasing RESPA parameters results in increasing efficiency at all core counts.
Graph 8 shows the speed up
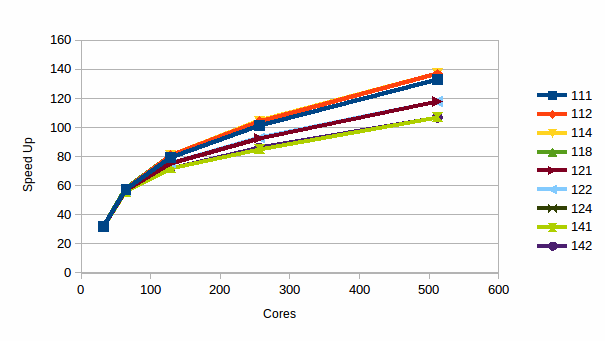
Graph
8: The Speed up for 69,120 atoms of a Sodium/Potassium Disilicate
glass
The final case considered is a simulation of 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC), a lipid, in water. This is a somewhat larger system at 413,896 atoms, and is more representative of the biochemical systems that RESPA was initially designed for. 512 timesteps were used in the runs, and as before the system was carefully equilibrated. This system has a large number of terms in the force field, and all four classes are represented:
Class 1: Harmonic bonds
Class 2: Angles, dihedrals
Class 3: Van der Waal's, short range Ewald
Class 4: Long range Ewald
Further some bonds are represented by constraints, and thus the SHAKE procedure is used within the integrator. Again we consider the quality of the simulation before looking at the efficiency and scalability.
Table 3 addresses the accuracy of the simulation on 128 cores
|
RESPA parameters |
Average Energy |
%Energy Difference |
RMS fluctuations in energy |
RMS/E |
Time |
% Time difference |
Timestep/s |
|
1:1:1 |
-5.362*105 |
0.00000 |
2.2869 |
-0.0000043 |
256.6 |
0.00 |
2.00 |
|
1:1:2 |
-5.362*105 |
-0.00187 |
2.2996 |
-0.0000043 |
234.7 |
-8.53 |
2.18 |
|
1:1:4 |
-5.362*105 |
-0.00187 |
2.5043 |
-0.0000047 |
223.6 |
-12.86 |
2.29 |
|
1:2:1 |
-5.362*105 |
-0.00187 |
3.3499 |
-0.0000062 |
164.6 |
-35.86 |
3.11 |
|
1:2:2 |
-5.362*105 |
-0.00373 |
3.5209 |
-0.0000066 |
153.2 |
-40.30 |
3.34 |
|
1:2:4 |
-5.361*105 |
-0.01492 |
7.8280 |
-0.0000146 |
148.2 |
-42.24 |
3.45 |
|
1:4:1 |
-5.360*105 |
-0.03917 |
35.9780 |
-0.0000671 |
118.2 |
-53.93 |
4.33 |
|
1:4:2 |
-5.359*105 |
-0.05595 |
35.8130 |
-0.0000668 |
117.7 |
-54.13 |
4.35 |
|
2:1:1 |
-5.361*105 |
-0.01306 |
11.6980 |
-0.0000218 |
157.6 |
-38.57 |
3.25 |
|
2:1:2 |
-5.361*105 |
-0.01306 |
11.5410 |
-0.0000215 |
146.8 |
-42.78 |
3.49 |
|
2:2:1 |
-5.359*105 |
-0.04663 |
28.8950 |
-0.0000539 |
111.5 |
-56.54 |
4.59 |
|
2:2:2 |
-5.358*105 |
-0.06528 |
32.7840 |
-0.0000611 |
105.9 |
-58.75 |
4.84 |
Table 3: DMPC in water on 128 cores
Again a similar story is seen, increasing RESPA parameters result in a decrease in simulation time, which in this case is particularly marked – if accuracy constraints are not very high it is possible to better than half the time required by the simulation.
Graphs 9 and 10 are again the efficiency and scalability of the calculation.
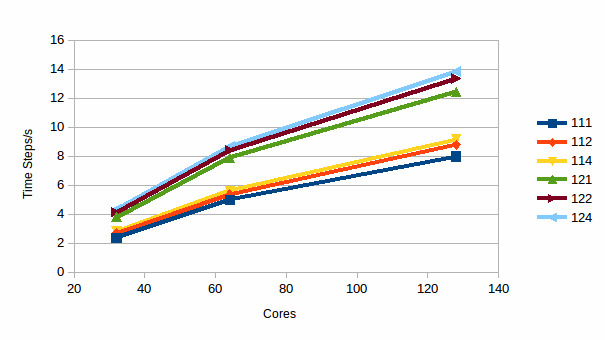
Graph
9: Timesteps/s for DMPC in water
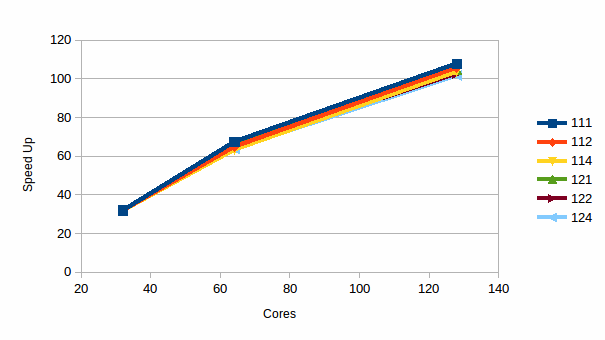
Graph
10: The Speed up for DMPC in water
As noted above the code has been completed for the NVE ensembles and 6 NVT ensembles, and as shown can improve the performance of the code markedly. Thus the intention is torrelease this code as soon as possible to the users as a large number of interesting cases can be considered using the work already performed.
For the remaining integrators, those for NPT simulations and involving rigid bodies, a follow up proposal has been submitted via the ARCHER eCSE mechanism. If successful this will complete the work presented here.
RESPA has been implemented for NVE and NVT integrators, both with and without constraints. It has been show that it can markedly increase the performance of the code for cases where it is applicable. A speed up of 20% is typical for a negligible decrease in accuracy, and cases where the code runs almost 2.5 times quicker whilst still generating sensible results have been demonstrated.
It should also be noted that another possibility would be to slightly decrease the timestep when using RESPA. Thus one would get some of the benefit of increased performance, but also regain some of the accuracy lost due to the method. This is an interesting possibility for practical calculations, but due to the size of the parameter space and time constraints we have not had time to investigate this during the project.
Two algorithmic improvements have been completed. In many ways they are similar in spirit in that they both attempt to avoid operations and in some cases communications by a “more intelligent” implementation of the of algorithms already used within DL_POLY_4. The first work package tuned the link cell algorithm to avoid recalculation of the Verlet neighbour list at every timestep. The second work package implemented the RESPA integration methodology, which avoids the calculation of slowly varying force terms every timestep. The first work package avoids some communications as particles need not be transferred to the ownership of a different process at each timestep. RESPA avoids communications where the force term does not fit exactly onto the domain decomposition used by DL_POLY_4, and thus requires communication.
These similarities carry through to the observed performance benefits. Both typically improve the performance of the code by 20-30%, but in ideal cases the increase can be a factor of 2 or more. Even for the user the similarity continues; to use both requires only a very small change to the input, but to get the best out of both methods will require a small amount of experimentation to determine the best padding or RESPA parameters.
So all in all two apparently disparate algorithms have been implemented, and both have been shown to provide similar, marked benefit to the efficiency of the code.
Ian Bush would like to thank Bill Smith for many useful and interesting conversations about molecular dynamics in general, and DL_POLY in particular.
This project was funded under the HECToR Distributed Computational Science and Engineering (CSE) Service operated by NAG Ltd. HECToR A Research Councils UK High End Computing Service – is the UK’s national supercomputing service, managed by EPSRC on behalf of the participating Research Councils. Its mission is to support capability science and engineering in UK academia. The HECToR supercomputers are managed by UoE HPCx Ltd and the CSE Support Service is provided by NAG Ltd. http://www.hector.ac.uk.
ivI.T. Todorov, W. Smith, K. Trachenko & M.T.Dove, J. Mater. Chem., 16, 1911-1918 (2006)
v I.J. Bush, I.T. Todorov and W. Smith, Comp. Phys. Commun., 175, 323-329 (2006)
vi M.R.S. Pinches, D. Tildesley, W. Smith, 1991, Mol Simulation, 6, 51
vii Tuckerman, Berne and Martyna, J. Chem. Phys., 97 (3), 1990-2001 (1992)
viii Humphrey, Freisner and Berne, J. Phys. Chem., 98, 6885-6892 (1994)
ix Courant, R.; Friedrichs, K.; Lewy, H. (1928), "Über die partiellen Differenzengleichungen der mathematischen Physik", Mathematische Annalen 100 (1): 32–74
xMartyna G. J., Tuckerman M. E., Tobias D. J., and Klein M. L., Mol. Phys. 87, 1117 (1996)