Parallelisation of the adaptive kinetic Monte Carlo code, DL_AKMC

David S.D. Gunn and John A. Purton

Scientific Computing Department

Science and Technology Facilities Council

Daresbury Laboratory, Sci-Tech Daresbury

Warrington, WA4 4AD

30^th September 2013

Abstract

The energy and force calculations in the adaptive kinetic Monte Carlo program, DL_AKMC, have been parallelised using MPI. A task-farm framework has been incorporated into the code to increase the efficiency of saddle-point evaluation. A confidence limit in the number of saddle points found has been included, and a variety of new potentials have also been added to increase the efficiency of the kinetic Monte Carlo algorithm, and to make the code relevant for a wide selection of materials and systems.

Table of Contents

1. Background.......................................................................................................................... 3

2. The dCSE Project and Objectives...................................................................................... 4

2.1 Parallel execution and improved efficiency of the saddle point searches........................ 5

2.2 Improving the efficiency of the energy/force calculations............................................... 6

2.3 Support for a variety of potential types............................................................................ 9

2.4 Defect detection algorithm............................................................................................. 10

2.5 Final reporting................................................................................................................. 11

3. Conclusions......................................................................................................................... 11

4. Acknowledgements............................................................................................................. 12

5. References........................................................................................................................... 12

1. Background

DL_AKMC is a universally applicable adaptive kinetic Monte Carlo (aKMC) program and is of use to a wide variety of disciplines. Kinetic Monte Carlo (KMC)¹ techniques are typically used to access long simulation timescales (up to the order of seconds). KMC constructs a list of possible system transition events (such as oxygen diffusion) and a move is made on every iteration of the KMC loop. The list of events can either be created prior to the simulation or calculated on the fly and we employ the latter approach since not all the events and defect configurations can be determined prior to the KMC simulation. Unfortunately, this makes the simulation more demanding since it is necessary to reliably determine possible events and the activation energies of these events and the time required to calculate these is significant. We have developed the methodology to examine diffusion of ionic materials over a few milliseconds in systems containing a few thousand ions (the overall simulation time is naturally system dependent). DL_AKMC was originally serial, and calculated the saddle points and activation energies sequentially. Under this dCSE grant, DL_AKMC has now been parallelised so that it can make use of the multicore architecture on HECToR and other HPC systems during the force/energy calculations.

The parallelisation has focussed on two main areas:

- Saddle point searches can now be performed on different nodes.

- Force/Energy calculations are parallelised with a combination of OpenMP and MPI.

DL_AKMC is applicable to many different areas of science. For example - the modelling of oxide ion diffusion and consequent ionic conductivity in fuel cell materials; investigating surface diffusion on ice mantles; determining healing timescales of materials damaged by radiation. The program is flexible and new methods for the calculation of activation energies can easily be incorporated and/or alternate methods for the calculation of the energies of the ions.

Our group, in collaboration with groups at Bristol and Sheffield universities, is currently employing atomistic computer simulations to identify suitable ceramic compounds for the storage of radioactive materials. Radioactive waste disposal is one of the greatest environmental challenges of the new century². The present total volume of radioactive waste in the UK is approximately 3.4 million m³ of which 1,100 m³ is high level waste (HLW)³. Moreover, the legacy of the Cold War requires the 'neutralisation' of approximately 1500 tonnes of Pu (half life of ²³⁹Pu is 24,100 years). The Committee on Radioactive Waste Management (CoRWM) recommendation of geological disposal of HLW⁴ has been accepted by the Government and has made the problem of safe disposal pressing.

Safe geological disposal requires that the radionuclides be bound in an inert matrix and buried deep below the Earth’s surfaces. This matrix must be capable of retaining its structural integrity during prolonged heavy particle bombardment at temperatures of 300-600 K. Also any host material must be resistant to radiation damage and leaching over timescales comparable to the half-life of the radionuclides.

Radiation damage events are modelled using a two step process. The first step employs molecular dynamics (MD) to “shoot” an energetic particle through the host material creating a cascade (ions are knocked away from their ideal lattice sites). The second step is to analyse the ability, if any, of the material to heal (diffusion of ions from defects back to their lattice sites). The latter process may take place over several seconds and is not amenable to study using MD (which is limited to timescales typically of the order ~1 ns). Instead, we use DL_AKMC.

2. The dCSE Project and Objectives

The code developed is an adaptive Kinetic Monte Carlo (aKMC) code. The aKMC method uses saddle-point searches and harmonic transition state theory to model rare-event, state-to-state dynamics in systems of interest. The dynamical events can be complex, involve many atoms and are not constrained to a grid – relaxing many of the conditions of regular KMC – making the code more versatile and useful in situations where the state transitions are not known a priori.

An aKMC simulation starts form an initially minimised configuration. From this state and all distinct states visited in the dynamics, saddle point searches are used to find the processes available to the system. For these searches we use the 'dimer' method⁵ as implemented in DL_FIND⁶, which can generally find saddle points within a few hundred energy evaluations. We are presently using the dimer method as it is robust and relatively efficient at calculating saddle point energies. However, the program has a modular construction and alternative methods can be included at a later stage without major reconstruction of the program. The dimer searches were initially consecutive, which was inefficient as there are no dependencies between saddle-point searches. As a result of this dCSE grant, the saddle point searches can now be distributed over multiple nodes, so that saddle point searches can be performed in parallel and independently of each other. Once all the saddle-point searches are completed the rates of the corresponding transitions are found using harmonic transition state theory, and the KMC algorithm advances the system to the next state, where the process is repeated. A comparison between the original (serial) and parallel versions of DL_AKMC is shown by the flowcharts in Figure 1.

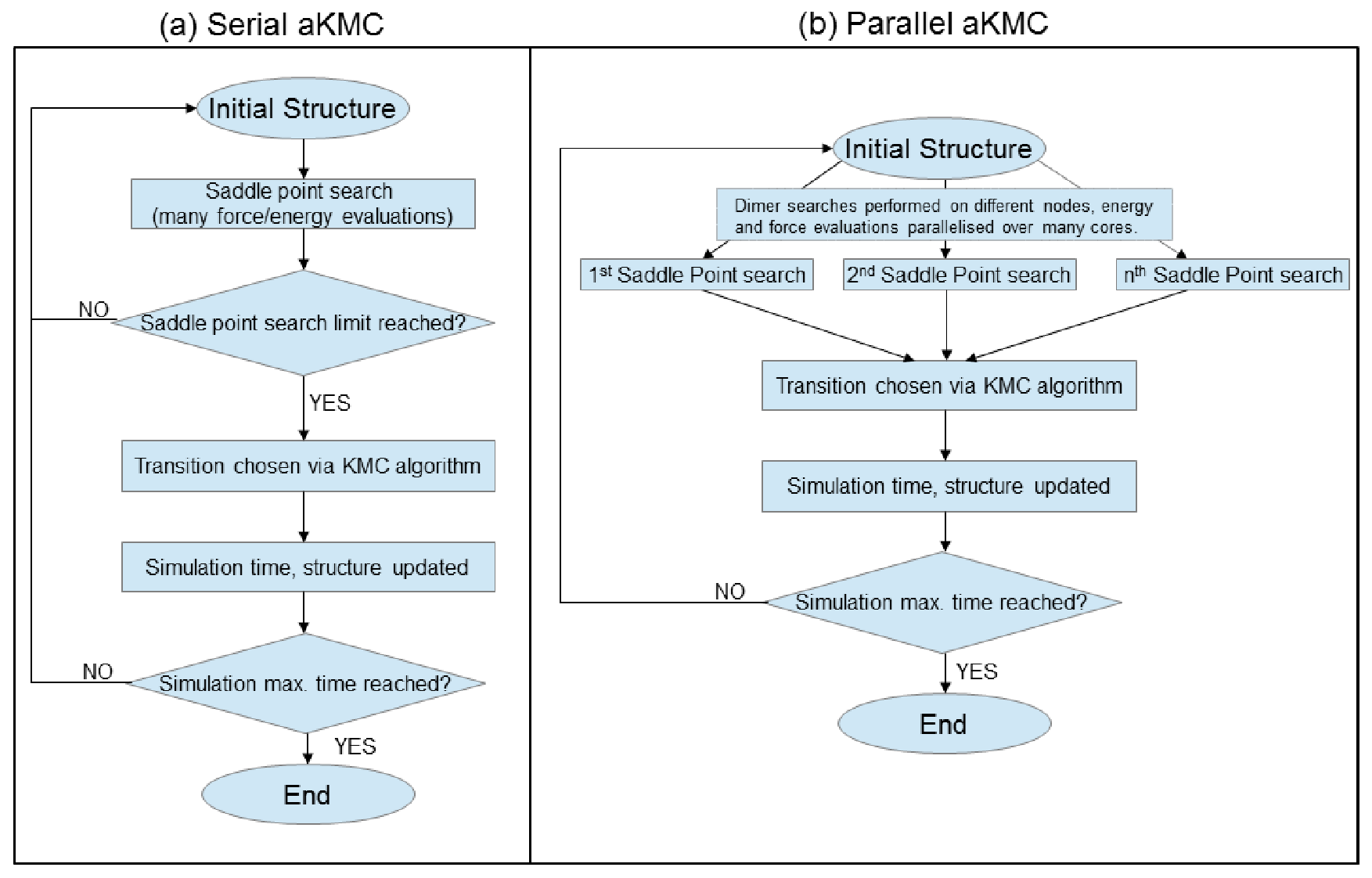
Figure 1: Workflow of the (a) serial aKMC program and (b) parallel aKMC program, with parallel distribution of saddle point searches and parallelisation of force/energy evaluations for each saddle point.

2.1 Parallel execution and improved efficiency of the saddle-point searches

Within a simulation cell the calculation of the activation energies of different transitions is achieved either by selecting atoms at random from the bulk mixture, selecting specific atoms from the bulk mixture, or activating the entire simulation cell prior to a dimer search. Originally DL_AKMC performed a set number of dimer searches for each state as defined by the user. This was typically 20-50 dimer searches for a system of approximately 1000 atoms. This process has now been improved with work packages (WP) 1.1 and 1.2.

WP 1.1: Distribution of saddle point searches over different nodes

In the serial program (Figure 1 (a)), saddle-point searches were performed over a loop with the next search not starting until the previous one is complete. As each search is independent, the efficiency can be greatly improved by distributing each saddle point search over a different node. We have implemented this “task farming” strategy by splitting the communicator⁷. The amount of data transferred between the nodes is small (the positions at the beginning and end of a saddle point search) and the overhead for communication is relatively small when compared to the time taken calculating the energies and forces.

Milestone 1.1: Demonstrate speed up gained by parallelisation of saddle point searches by comparing serial performance against dimer-parallelised performance for a small (~2k atoms) radiation-damaged system. 20 dimer searches will be performed for each system state, and the parallel code will be run on 1, 2, 4, 16 and 32 cores of HECToR. The total simulation time reached after 12 hours will be compared.

Outcome 1.1: Saddle points can now be distributed over different nodes – as defined by the user in the control file. The metrics for this milestone are somewhat spurious, as you naturally achieve a 100% (or very near) speedup with each additional core, as each core is performing its own independent saddle point search.

WP 1.2: Confidence limit for the number of dimer searches

To minimise the number of dimer searches we have incorporated a confidence level for each state that can describe the probability that an important saddle point has been missed. This confidence level provides a dynamic criterion to decide when sufficient saddle-point searches have been made and therefore speed up the code by eliminating unnecessary saddle-point searches. Suitable algorithms have been proposed by Xu and Henkelman⁸.

Milestone 1.2: Demonstrate the speed up gained by the implementation of the confidence limit for the saddle point searches, using the system described in Milestone 1.1, and comparing the total simulation time reached for the fixed 20-dimer searches per system state (12 hours, 5 nodes of HECToR), with that attained with the confidence limit imposed under the same conditions.

Outcome 1.2: The confidence limit has been implemented and a user can specify in the control file the level of confidence required before the system will progress to the next state. The implementation of the confidence limit does not inherently speed up the code, instead it gives a certain confidence that the simulation is performing at a specified level of accuracy. If the user specified, for example, only 5 dimer searches to be performed for each saddle point the simulation would proceed quickly (compared to one with a high confidence limit), but the kinetics would be questionable.

2.2 Improving the efficiency of the energy/force calculations

Each saddle point search requires multiple computations of the system energy and of the forces on the atoms/ions (approximately 100 computations per saddle-point search) and is the most time consuming part of the calculation. As part of the dCSE grant we have taken advantage of the multicore architecture of HECToR and have modified DL_AKMC so that the energies/forces are calculated on at least one node using a combination of OpenMP and MPI.

WP 2.1: Incorporate OpenMP/MPI in the energy/force calculations

The energy and force calculations primarily run over several nested ‘DO’-loops, which evaluate functions based upon the distance between an atom and every other atom in the system. This process is repeated over every atom in the system to determine the total system energy and individual forces on each atom. This section of the code has been made more efficient by parallelisation via replicated data using OpenMP and MPI, and has made the code suitable for efficiently investigating systems larger than ~1000 atoms. Each dimer search can be distributed to a node(s) on HECToR (or other HPC system), and the energy/force evaluations can be distributed over each core by a combination of OpenMP and MPI. An additional improvement not originally planned as part of this grant has also been included – that of a neighbour list. This increases the efficiency of the force/energy calculations by establishing a list of neighbours for each atom so that evaluations over the entire cell can be minimised.

Milestone 2.1: Demonstrate the speed up gained with the OpenMP/MPI implementation in the force/energy calculations by comparing the total simulation time reached for the system in Milestone 1.2 (confidence limit, parallel dimer searches, 12 hours, 5 nodes HECToR), with the simulation time reached under the same conditions and with the OpenMP/MPI implementation included.

Outcome 2.1: OpenMP and MPI have been incorporated in the force/energy calculations, currently MPI-only is default. Due to the random nature of the code total simulation time comparison is not the best means of comparison. Instead, we have compared the speed up between a serial calculation and parallel calculations in evaluating 200 energy and force evaluations of a system (Gd₂Ti₂O₇) that has ~2000 ions. The parallel calculations use 2, 4, 8, 16 and 32 cores for each force/energy evaluation. Results are shown in Figure 2.

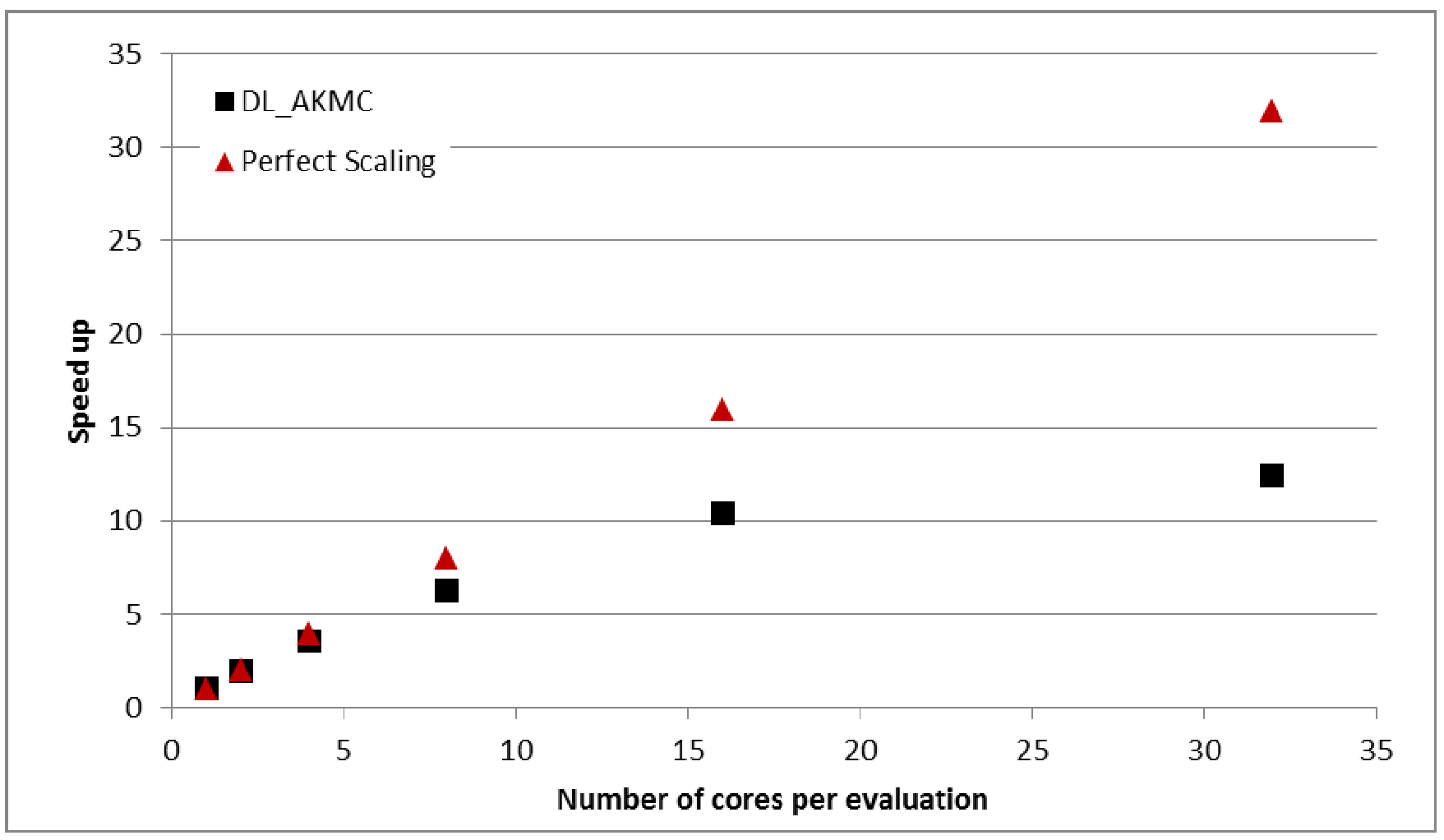
Figure 2: Speed up between serial and parallel calculations for 200 force/energy evaluations in a ~2000 ion Gd₂Ti₂O₇ system.

From Figure 2 we can see that the parallelisation of the force/energy evaluations in DL_AKMC scales well up to 8 cores, at which point communication overheads slow down the simulation. This is useful to know, as the setup can be optimised such that dimer searches can be task-farmed to blocks of 8 cores to maximise the number and efficiency of dimer searches for a given number of available cores. We have identified many areas in which this parallelisation and scalability can be improved, however we lacked time to implement these under this grant.

Milestone 2.2: Demonstrate scalability of the code by comparing simulations of different radiation-damaged system sizes (~2k, 20k, 200k atoms) over different numbers of cores on HECToR (1, 128, 1024, 2048, 4096, 8192). Scalability will be determined by comparing the total simulation time reached after 12 hours in each case.

Outcome 2.2: DL_AKMC is designed to be used in such a way that maximises both the number of dimer searches that can be performed in parallel, and the number of cores used per energy/force evaluation. Measuring the scalability over a small number of cores is therefore more relevant than investigating the scalability of performing single dimer searches over a large number of cores. Milestone 2.2 was modified to reflect this by comparing the time taken to evaluate 200 energy and force evaluations of Gd₂Ti₂O₇ systems that have ~2k, ~20k and ~200k ions with 2, 4, 8, 16 and 32 cores. The results are shown in Figure 3.

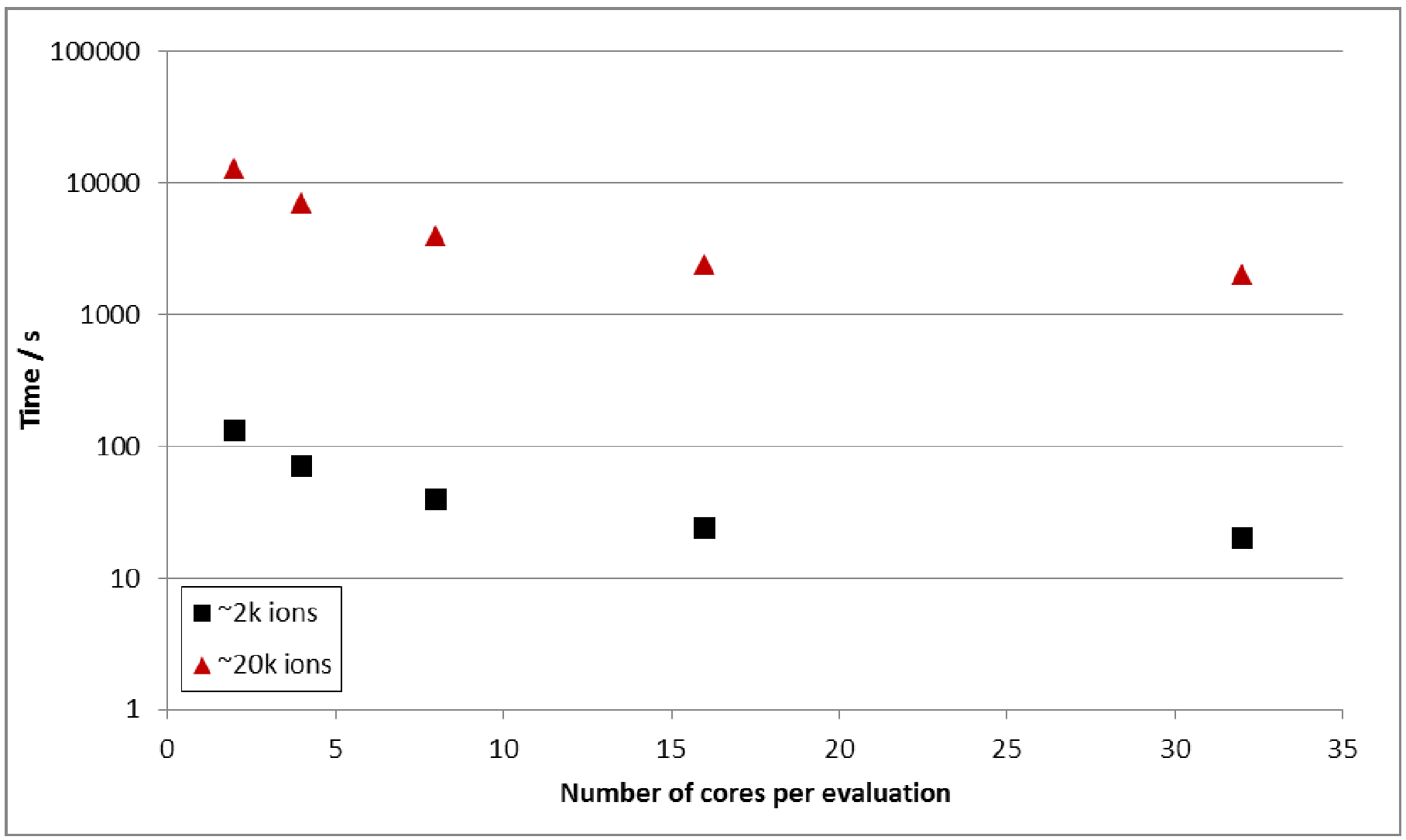
Figure 3: Time taken for 200 force/energy evaluations in a ~2k and ~20k ion Gd₂Ti₂O₇ systems.

Simulations of the ~200k ion system did not complete 200 energy/force evaluations within the 12 hour time limit on the queue and so no data for this system is shown in Figure 3. Scalability appears to be approximately of O(n²).

2.3 Support for a variety of potential types

The code originally only supported one type of short ranged potential (Buckingham) to describe the 2-body interaction between ions in the system. We have now added a more diverse suite of potentials – including Embedded Atom Method and Tersoff potentials, substantially increasing the usefulness of the code to a wider range of users.

WP 3.1: Tersoff potential

The Tersoff potential is a special example of a density dependent potential, which has been designed to reproduce the properties of covalent bonding in systems containing carbon, silicon, germanium etc. and alloys of these elements. A special feature of the potential is that it allows bond breaking and associated changes in bond hybridisation. This potential is of great use for the semi-conductor modelling community.

Milestone 3.1: Demonstrate the working Tersoff potential by comparing the system energy and forces calculated for a 512 atom carbon (diamond) system with the DL_AKMC and with DL_POLY.

Outcome 3.1: This has been done, and the energy and forces match between DL_AKMC and DL_POLY Classic.

WP 3.2: Embedded atom method (EAM)

The EAM potential is a density dependent potential derived from density functional theory and describes the bonding of a metal atom ultimately in terms of the local electronic density. This type of potential is especially useful in describing the properties of metals and metal alloys and therefore of use to a wide selection of researchers.

Milestone 3.2: Demonstrate the working EAM potential by comparing the system energy and forces calculated for a 256 atom aluminium system with the aKMC code and with DL_POLY.

Outcome 3.2: This has been done, and the energy and forces match between DL_AKMC and DL_POLY Classic.

2.4 Defect detection algorithm

Within a simulation cell the calculation of the activation energies of different transitions is achieved either by selecting atoms at random from the bulk mixture, selecting specific atoms from the bulk mixture, or activating the entire simulation cell prior to a dimer search. These methods have obvious impact on the number of dimer searches required and hence the time taken for simulation as a whole. Therefore, intelligent selection of ions at this stage in the program could dramatically reduce the number of saddle point searches and computational wall time.

The lowest energy atomic transitions are typically those located around defective areas in a material. To speed up an aKMC calculation the saddle-point searches can be localised around such areas to find a high proportion of low-energy transitions, which would be the most likely to occur in any given KMC step. In a large system (many thousands of atoms), with many randomised defective areas (as you would have from a sample damaged by radiation) such areas are hard to pinpoint. A suitable defect detection algorithm is required that can automate the process of identifying defective areas of the material and then proceed with a localised saddle-point search.

WP 4.1: Include Steinhardt order parameters

We had proposed to use the method developed by Allan and co-workers to identify defective environments in pyrochlores, as this would greatly speed up the simulation of healing in such materials and would also give us a means to identify low energy transitions. The method is based on the calculation of local bond order parameters based on spherical harmonics (also known as Steinhardt order parameters⁹), and has been adapted from similar approaches used to analyse the structure of crystalline clusters, soft particle systems and supercooled liquids.

Milestone 4.1: Demonstrate speed up gained from the implementation of the Steinhardt order parameters to target local defective sites, by comparing the total simulation time reached for the system in Milestone 2.1 (OpenMP/MPI, confidence limit, parallel dimer searches, 12 hours, 5 nodes HECToR), with the simulation time reached under the same conditions and with the Steinhardt order parameter implementation included.

Outcome 4.1: We have been unable to implement the Steinhardt order parameters as we intended. The algorithm is complex and the method could not be refined enough to be robust and general purpose in the time available. We are keen to pursue this improvement and intend to include it in a later release of the code. Once it was identified that this work package was unachievable in the time available, effort was focussed on other areas of improvement such as including a neighbour list and increasing the general efficiency and usability of the code.

2.5 Final reporting

WP 5.2: Produce user manual for aKMC program

Milestone 5.2: User manual written and available online.

Outcome 5.2: The user manual will be available on the CCPForge website (http://ccpforge.cse.rl.ac.uk/gf/project/kmc/ ).

3. Conclusions

The substantial improvement of DL_AKMC via parallel execution of processes to determine transition states and the incorporation of OpenMP and MPI in the energy/force calculations has extended both the length and timescales that are able to be studied by this technique and this has had an immediate benefit in our research on radiation damage in materials. The damage is created using molecular dynamics (MD) and large system sizes are a prerequisite, as this helps eliminate cascades interacting with the periodic image and sound waves from travelling through the periodic boundary conditions. MD cannot be used to study the subsequent healing of the material and the availability of DL_AKMC for use with larger systems enables us to take input from MD simulations rather than concentrating on model systems. Therefore, the parallelisation of DL_AKMC allows the healing of these large systems to be modelled on a realistic timescale.

DL_AKMC will be of wide use to many members of the materials science modelling community, especially with the additional inclusion of a more diverse suite of potentials. The versatility and universal applicability of the code will help researchers in e.g. modelling diffusion through different electrolyte materials for fuel cell applications, looking at the recombination of adatoms on a surface for catalysis, thin film growth or even simulating diffusion in interstellar ices. In the near future, DL_AKMC will be a vital part of EPSRC grant EP/K016288/1, modelling materials of interest to the energy sector. DL_AKMC is available under a GNU Lesser General Public Licence (LGPL), enabling interested members of the community to download and modify the code for non-commercial use.

4. Acknowledgements

This project was funded under the HECToR Distributed Computational Science and Engineering (CSE) Service operated by NAG Ltd. HECToR – A Research Councils UK High End Computing Service – is the UK’s national supercomputing service, managed by EPSRC on behalf of the participating Research Councils. Its mission is to support capability science and engineering in UK academia. The HECToR supercomputers are managed by UoE HPCx Ltd. and the CSE Support Service is provided by NAG Ltd. http://www.hector.ac.uk .

5. References

[1] M.R. Sorenson and A.F. Voter, J. Chem. Phys. 112 (2000) 9599

[2] Royal Society Policy Document 24/07 Strategy options for the UK’s separated plutonium: http://royalsociety.org/displaypagedoc.asp?id=27169

[3] Nuclear Decommissioning Authority report, NDA/RWMD/003 (2008)

[4] Committee on Radioactive Waste Management (CoRWM) report 700: Recommendations to Government.

[5] G. Henkelman and H. Jónsson, J. Chem. Phys. 111 (1999) 7010

[6] J. Kästner, J.M. Carr, T.W. Keal, W. Thiel, A.Wander and P. Sherwood, J. Phys. Chem. A 113 (2009) 11856

[7] W. Gropp, E. Lusk and A. Skjellum, Using MPI: Portable Parellel Programming with Message Passing Interface, MIT Press (1999) page 61

[8] L. Xu and G. Henkelman, J. Chem. Phys. 129 (2008) 114104

[9] P. Steinhardt, D.R. Nelson and M. Ronchetti, Phys. Rev. B 28 (1983) 784

[10] A.F. Voter, Phys. Rev. B34 (1986) 6819